Extracting Root Element From Heap

Table of content

Extract method is used to extract the root element of a Heap. Following is the algorithm.

Pseudocode

Heap-Extract-Max (numbers[]) 
max = numbers[1] 
numbers[1] = numbers[heapsize] 
heapsize = heapsize – 1 
Max-Heapify (numbers[], 1) 
return max

Example

Let us consider the same example discussed previously. Now we want to extract an element. This method will return the root element of the heap.

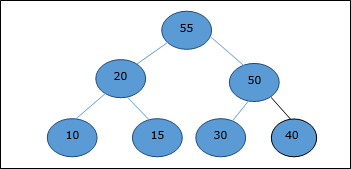
Method

After deletion of the root element, the last element will be moved to the root position.

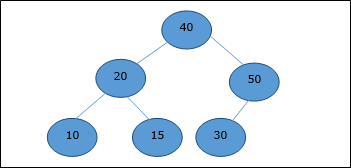
Root Element

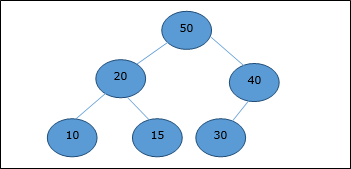
Now, Heapify function will be called. After Heapify, the following heap is generated.

Heapify

Implementation

Following are the implementations of this operation in various programming languages −

C C++ Java Python 
#include <stdio.h>
void swap(int arr[], int i, int j) {
   int temp = arr[i];
   arr[i] = arr[j];
   arr[j] = temp;
}
void maxHeapify(int arr[], int size, int i) {
   int leftChild = 2 * i + 1;
   int rightChild = 2 * i + 2;
   int largest = i;
   if (leftChild < size && arr[leftChild] > arr[largest])
      largest = leftChild;
   if (rightChild < size && arr[rightChild] > arr[largest])
      largest = rightChild;
   if (largest != i) {
      swap(arr, i, largest);
      maxHeapify(arr, size, largest); // Recursive call to continue heapifying
   }
}
int extractMax(int arr[], int *heapSize) {
   if (*heapSize < 1) {
      printf("Heap underflow!\n");
      return -1;
   }
   int max = arr[0];
   arr[0] = arr[*heapSize - 1];
   (*heapSize)--;
   maxHeapify(arr, *heapSize, 0); // Heapify the updated heap
   return max;
}
int main() {
   int arr[] = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
   int heapSize = sizeof(arr) / sizeof(arr[0]);
   int max = extractMax(arr, &heapSize); // Extract the max element from the heap
   printf("Extracted Max Element: %d\n", max);
   // Print the updated Max-Heap
   printf("Updated Max-Heap: ");
   for (int i = 0; i < heapSize; i++)
       printf("%d ", arr[i]);
   printf("\n");
   return 0;
}

Output

Extracted Max Element: 55
Updated Max-Heap: 50 40 30 10 20 15 

#include <iostream>
#include <vector>
void swap(std::vector<int>& arr, int i, int j) {
   int temp = arr[i];
   arr[i] = arr[j];
   arr[j] = temp;
}
void maxHeapify(std::vector<int>& arr, int size, int i) {
   int leftChild = 2 * i + 1;
   int rightChild = 2 * i + 2;
   int largest = i;
   if (leftChild < size && arr[leftChild] > arr[largest])
      largest = leftChild;
   
   if (rightChild < size && arr[rightChild] > arr[largest])
      largest = rightChild;
   if (largest != i) {
      swap(arr, i, largest);
      maxHeapify(arr, size, largest); // Recursive call to continue heapifying
   }
}
int extractMax(std::vector<int>& arr, int& heapSize) {
   if (heapSize < 1) {
      std::cout << "Heap underflow!" << std::endl;
      return -1;
   }
   int max = arr[0];
   arr[0] = arr[heapSize - 1];
   heapSize--;
   maxHeapify(arr, heapSize, 0); // Heapify the updated heap
   return max;
}
int main() {
   std::vector<int> arr = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
   int heapSize = arr.size();
   int max = extractMax(arr, heapSize); // Extract the max element from the heap
   std::cout << "Extracted Max Element: " << max << std::endl;
   // Print the updated Max-Heap
   std::cout << "Updated Max-Heap: ";
   for (int i = 0; i < heapSize; i++)
       std::cout << arr[i] << " ";
   std::cout << std::endl;
   return 0;
}

Output

Extracted Max Element: 55
Updated Max-Heap: 50 40 30 10 20 15 

import java.util.Arrays;
public class MaxHeap {
   public static void swap(int arr[], int i, int j) {
      int temp = arr[i];
      arr[i] = arr[j];
      arr[j] = temp;
   }
   public static void maxHeapify(int arr[], int size, int i) {
      int leftChild = 2 * i + 1;
      int rightChild = 2 * i + 2;
      int largest = i;
      if (leftChild < size && arr[leftChild] > arr[largest])
         largest = leftChild;
      if (rightChild < size && arr[rightChild] > arr[largest])
         largest = rightChild;
      if (largest != i) {
         swap(arr, i, largest);
         maxHeapify(arr, size, largest); // Recursive call to continue heapifying
      }
   }
   public static int extractMax(int arr[], int heapSize) {
      if (heapSize < 1) {
          System.out.println("Heap underflow!");
          return -1;
      }
      int max = arr[0];
      arr[0] = arr[heapSize - 1];
      heapSize--;
      maxHeapify(arr, heapSize, 0); // Heapify the updated heap
      return max;
      }
public static void main(String args[]) {
   int arr[] = { 55, 50, 30, 40, 20, 15, 10 }; // Max-Heap
   int heapSize = arr.length;
   int max = extractMax(arr, heapSize); // Extract the max element from the heap
   System.out.println("Extracted Max Element: " + max);
   // Print the updated Max-Heap
   System.out.print("Updated Max-Heap: ");
   for (int i = 0; i < heapSize; i++)
      System.out.print(arr[i] + " ");
   System.out.println();
   }
}

Output

Extracted Max Element: 55
Updated Max-Heap: 50 40 30 10 20 15 10 

def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]
def max_heapify(arr, size, i):
    left_child = 2 * i + 1
    right_child = 2 * i + 2
    largest = i
    if left_child < size and arr[left_child] > arr[largest]:
        largest = left_child
    if right_child < size and arr[right_child] > arr[largest]:
        largest = right_child
    if largest != i:
        swap(arr, i, largest)
        max_heapify(arr, size, largest) # Recursive call to continue heapifying
def extract_max(arr, heap_size):
    if heap_size < 1:
        print("Heap underflow!")
        return -1
    max_element = arr[0]
    arr[0] = arr[heap_size - 1]
    heap_size -= 1
    max_heapify(arr, heap_size, 0) # Heapify the updated heap
    return max_element
arr = [55, 50, 30, 40, 20, 15, 10] # Max-Heap
heap_size = len(arr)
max_element = extract_max(arr, heap_size) # Extract the max element from the heap
print("Extracted Max Element:", max_element)
# Print the updated Max-Heap
print("Updated Max-Heap:", arr)

Output

Extracted Max Element: 55
Updated Max-Heap: [50, 40, 30, 10, 20, 15, 10]
Advertisements