
- Data Structures & Algorithms
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Tries
- DSA - Heap Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Subsequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Merge Sort Algorithm
Merge sort is a sorting technique based on divide and conquer technique. With worst-case time complexity being Ο(n log n), it is one of the most used and approached algorithms.
Merge sort first divides the array into equal halves and then combines them in a sorted manner.
How Merge Sort Works?
To understand merge sort, we take an unsorted array as the following −

We know that merge sort first divides the whole array iteratively into equal halves unless the atomic values are achieved. We see here that an array of 8 items is divided into two arrays of size 4.

This does not change the sequence of appearance of items in the original. Now we divide these two arrays into halves.

We further divide these arrays and we achieve atomic value which can no more be divided.

Now, we combine them in exactly the same manner as they were broken down. Please note the color codes given to these lists.
We first compare the element for each list and then combine them into another list in a sorted manner. We see that 14 and 33 are in sorted positions. We compare 27 and 10 and in the target list of 2 values we put 10 first, followed by 27. We change the order of 19 and 35 whereas 42 and 44 are placed sequentially.

In the next iteration of the combining phase, we compare lists of two data values, and merge them into a list of found data values placing all in a sorted order.

After the final merging, the list becomes sorted and is considered the final solution.

Merge Sort Algorithm
Merge sort keeps on dividing the list into equal halves until it can no more be divided. By definition, if it is only one element in the list, it is considered sorted. Then, merge sort combines the smaller sorted lists keeping the new list sorted too.
Step 1: If it is only one element in the list, consider it already sorted, so return. Step 2: Divide the list recursively into two halves until it can no more be divided. Step 3: Merge the smaller lists into new list in sorted order.
Pseudocode
We shall now see the pseudocodes for merge sort functions. As our algorithms point out two main functions − divide & merge.
Merge sort works with recursion and we shall see our implementation in the same way.
procedure mergesort( var a as array )
if ( n == 1 ) return a
var l1 as array = a[0] ... a[n/2]
var l2 as array = a[n/2+1] ... a[n]
l1 = mergesort( l1 )
l2 = mergesort( l2 )
return merge( l1, l2 )
end procedure
procedure merge( var a as array, var b as array )
var c as array
while ( a and b have elements )
if ( a[0] > b[0] )
add b[0] to the end of c
remove b[0] from b
else
add a[0] to the end of c
remove a[0] from a
end if
end while
while ( a has elements )
add a[0] to the end of c
remove a[0] from a
end while
while ( b has elements )
add b[0] to the end of c
remove b[0] from b
end while
return c
end procedure
Example
In the following example, we have shown Merge-Sort algorithm step by step. First, every iteration array is divided into two sub-arrays, until the sub-array contains only one element. When these sub-arrays cannot be divided further, then merge operations are performed.
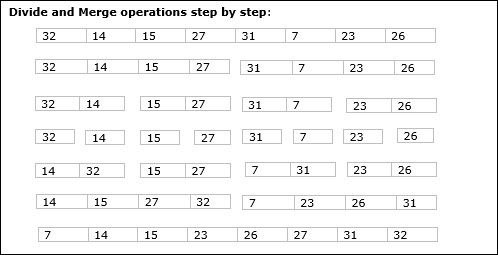
Analysis
Let us consider, the running time of Merge-Sort as T(n). Hence,
$$\mathrm{T\left ( n \right )=\left\{\begin{matrix} c & if\, n\leq 1 \\ 2\, xT\left ( \frac{n}{2} \right )+dxn &otherwise \\ \end{matrix}\right.}\:where\: c\: and\: d\: are\: constants$$
Therefore, using this recurrence relation,
$$T\left ( n \right )=2^{i}\, T\left ( n/2^{i} \right )+i\cdot d\cdot n$$
$$As,\:\: i=log\: n,\: T\left ( n \right )=2^{log\, n}T\left ( n/2^{log\, n} \right )+log\, n\cdot d\cdot n$$
$$=c\cdot n+d\cdot n\cdot log\: n$$
$$Therefore,\: \: T\left ( n \right ) = O(n\: log\: n ).$$
Example
Following are the implementations of the above approach in various programming languages −
#include <stdio.h>
#define max 10
int a[11] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
int b[10];
void merging(int low, int mid, int high){
int l1, l2, i;
for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
if(a[l1] <= a[l2])
b[i] = a[l1++];
else
b[i] = a[l2++];
}
while(l1 <= mid)
b[i++] = a[l1++];
while(l2 <= high)
b[i++] = a[l2++];
for(i = low; i <= high; i++)
a[i] = b[i];
}
void sort(int low, int high){
int mid;
if(low < high) {
mid = (low + high) / 2;
sort(low, mid);
sort(mid+1, high);
merging(low, mid, high);
} else {
return;
}
}
int main(){
int i;
printf("Array before sorting\n");
for(i = 0; i <= max; i++)
printf("%d ", a[i]);
sort(0, max);
printf("\nArray after sorting\n");
for(i = 0; i <= max; i++)
printf("%d ", a[i]);
}
Output
Array before sorting 10 14 19 26 27 31 33 35 42 44 0 Array after sorting 0 10 14 19 26 27 31 33 35 42 44
#include <iostream>
using namespace std;
#define max 10
int a[11] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
int b[10];
void merging(int low, int mid, int high){
int l1, l2, i;
for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
if(a[l1] <= a[l2])
b[i] = a[l1++];
else
b[i] = a[l2++];
}
while(l1 <= mid)
b[i++] = a[l1++];
while(l2 <= high)
b[i++] = a[l2++];
for(i = low; i <= high; i++)
a[i] = b[i];
}
void sort(int low, int high){
int mid;
if(low < high) {
mid = (low + high) / 2;
sort(low, mid);
sort(mid+1, high);
merging(low, mid, high);
} else {
return;
}
}
int main(){
int i;
cout << "Array before sorting\n";
for(i = 0; i <= max; i++)
cout<<a[i]<<" ";
sort(0, max);
cout<< "\nArray after sorting\n";
for(i = 0; i <= max; i++)
cout<<a[i]<<" ";
}
Output
Array before sorting 10 14 19 26 27 31 33 35 42 44 0 Array after sorting 0 10 14 19 26 27 31 33 35 42 44
public class Merge_Sort {
static int a[] = { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0 };
static int b[] = new int[a.length];
static void merging(int low, int mid, int high) {
int l1, l2, i;
for(l1 = low, l2 = mid + 1, i = low; l1 <= mid && l2 <= high; i++) {
if(a[l1] <= a[l2])
b[i] = a[l1++];
else
b[i] = a[l2++];
}
while(l1 <= mid)
b[i++] = a[l1++];
while(l2 <= high)
b[i++] = a[l2++];
for(i = low; i <= high; i++)
a[i] = b[i];
}
static void sort(int low, int high) {
int mid;
if(low < high) {
mid = (low + high) / 2;
sort(low, mid);
sort(mid+1, high);
merging(low, mid, high);
} else {
return;
}
}
public static void main(String args[]) {
int i;
int n = a.length;
System.out.println("Array before sorting");
for(i = 0; i < n; i++)
System.out.print(a[i] + " ");
sort(0, n-1);
System.out.println("\nArray after sorting");
for(i = 0; i < n; i++)
System.out.print(a[i]+" ");
}
}
Output
Array before sorting 10 14 19 26 27 31 33 35 42 44 0 Array after sorting 0 10 14 19 26 27 31 33 35 42 44
def merge_sort(a, n):
if n > 1:
m = n // 2
#divide the list in two sub lists
l1 = a[:m]
n1 = len(l1)
l2 = a[m:]
n2 = len(l2)
#recursively calling the function for sub lists
merge_sort(l1, n1)
merge_sort(l2, n2)
i = j = k = 0
while i < n1 and j < n2:
if l1[i] <= l2[j]:
a[k] = l1[i]
i = i + 1
else:
a[k] = l2[j]
j = j + 1
k = k + 1
while i < n1:
a[k] = l1[i]
i = i + 1
k = k + 1
while j < n2:
a[k]=l2[j]
j = j + 1
k = k + 1
a = [10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0]
n = len(a)
print("Array before Sorting")
print(a)
merge_sort(a, n)
print("Array after Sorting")
print(a)
Output
Array before Sorting [10, 14, 19, 26, 27, 31, 33, 35, 42, 44, 0] Array after Sorting [0, 10, 14, 19, 26, 27, 31, 33, 35, 42, 44]
