Insertion Sort Algorithm

Insertion sort is a very simple method to sort numbers in an ascending or descending order. This method follows the incremental method. It can be compared with the technique how cards are sorted at the time of playing a game.

This is an in-place comparison-based sorting algorithm. Here, a sub-list is maintained which is always sorted. For example, the lower part of an array is maintained to be sorted. An element which is to be 'inserted' in this sorted sub-list, has to find its appropriate place and then it has to be inserted there. Hence the name, insertion sort.

The array is searched sequentially and unsorted items are moved and inserted into the sorted sub-list (in the same array). This algorithm is not suitable for large data sets as its average and worst case complexity are of Ο(n²), where n is the number of items.

Insertion Sort Algorithm

Now we have a bigger picture of how this sorting technique works, so we can derive simple steps by which we can achieve insertion sort.

Step 1 − If it is the first element, it is already sorted. return 1;

Step 2 − Pick next element

Step 3 − Compare with all elements in the sorted sub-list

Step 4 − Shift all the elements in the sorted sub-list that is greater than the value to be sorted

Step 5 − Insert the value

Step 6 − Repeat until list is sorted

Pseudocode

Algorithm: Insertion-Sort(A)
for j = 2 to A.length
   key = A[j]
   i = j – 1
   while i > 0 and A[i] > key
      A[i + 1] = A[i]
      i = i -1
   A[i + 1] = key

Analysis

Run time of this algorithm is very much dependent on the given input.

If the given numbers are sorted, this algorithm runs in O(n) time. If the given numbers are in reverse order, the algorithm runs in O(n²) time.

Example

We take an unsorted array for our example.

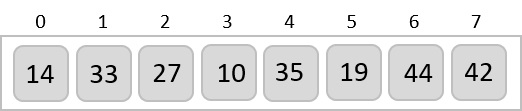
Insertion sort compares the first two elements.

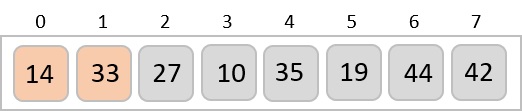
It finds that both 14 and 33 are already in ascending order. For now, 14 is in sorted sub-list.

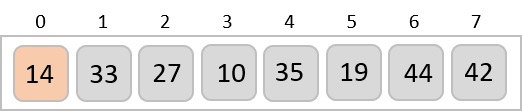
Insertion sort moves ahead and compares 33 with 27.

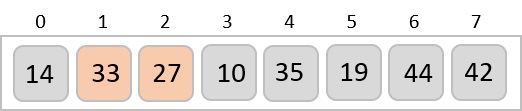
And finds that 33 is not in the correct position. It swaps 33 with 27. It also checks with all the elements of sorted sub-list. Here we see that the sorted sub-list has only one element 14, and 27 is greater than 14. Hence, the sorted sub-list remains sorted after swapping.

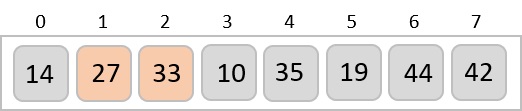
By now we have 14 and 27 in the sorted sub-list. Next, it compares 33 with 10. These values are not in a sorted order.

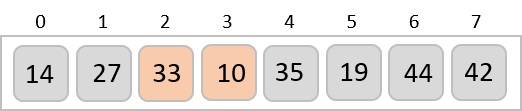
So they are swapped.

However, swapping makes 27 and 10 unsorted.

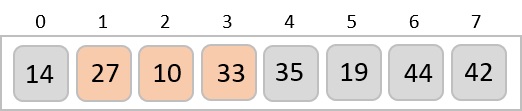
Hence, we swap them too.

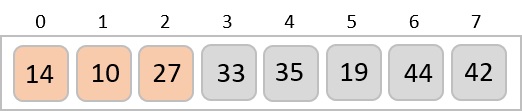
Again we find 14 and 10 in an unsorted order.

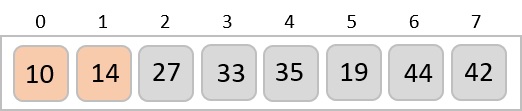
We swap them again.

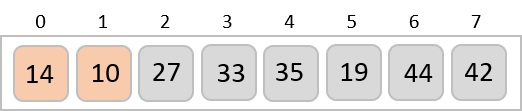
By the end of third iteration, we have a sorted sub-list of 4 items.

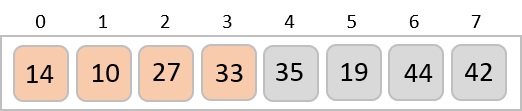
This process goes on until all the unsorted values are covered in a sorted sub-list. Now we shall see some programming aspects of insertion sort.

Implementation

Since insertion sort is an in-place sorting algorithm, the algorithm is implemented in a way where the key element – which is iteratively chosen as every element in the array – is compared with it consequent elements to check its position. If the key element is less than its successive element, the swapping is not done. Otherwise, the two elements compared will be swapped and the next element is chosen as the key element.

Insertion sort is implemented in four programming languages, C, C++, Java, and Python −

#include <stdio.h>
void insertionSort(int array[], int size){
   int key, j;
   for(int i = 1; i<size; i++) {
      key = array[i];//take value
      j = i;
      while(j > 0 && array[j-1]>key) {
         array[j] = array[j-1];
         j--;
      }
      array[j] = key; //insert in right place
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {67, 44, 82, 17, 20}; // initialize the array
   printf("Array before Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ",arr[i]);
   printf("\n");
   insertionSort(arr, n);
   printf("Array after Sorting: ");
   for(int i = 0; i<n; i++)
      printf("%d ", arr[i]);
   printf("\n");
}

Array before Sorting: 67 44 82 17 20 
Array after Sorting: 17 20 44 67 82 

#include<iostream>
using namespace std;
void insertionSort(int *array, int size){
   int key, j;
   for(int i = 1; i<size; i++) {
      key = array[i];//take value
      j = i;
      while(j > 0 && array[j-1]>key) {
         array[j] = array[j-1];
         j--;
      }
      array[j] = key; //insert in right place
   }
}
int main(){
   int n;
   n = 5;
   int arr[5] = {67, 44, 82, 17, 20}; // initialize the array
   cout << "Array before Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
   insertionSort(arr, n);
   cout << "Array after Sorting: ";
   for(int i = 0; i<n; i++)
      cout << arr[i] << " ";
   cout << endl;
}

Array before Sorting: 67 44 82 17 20
Array after Sorting: 17 20 44 67 82

import java.io.*;
public class InsertionSort {
   public static void main(String args[]) {
      int n = 5;
      int[] arr = {67, 44, 82, 17, 20}; //initialize an array
      System.out.print("Array before Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
      for(int i = 1; i<n; i++) {
         int key = arr[i];//take value
         int j = i;
         while(j > 0 && arr[j-1]>key) {
            arr[j] = arr[j-1];
            j--;
         }
         arr[j] = key; //insert in right place
      }
      System.out.print("Array After Sorting: ");
      for(int i = 0; i<n; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

Array before Sorting: 67 44 82 17 20
Array After Sorting: 17 20 44 67 82

def insertion_sort(array, size):
   for i in range(1, size):
      key = array[i]
      j = i
      while (j > 0) and (array[j-1] > key):
         array[j] = array[j-1]
         j = j-1
      array[j] = key
      
arr = [67, 44, 82, 17, 20]
n = len(arr)
print("Array before Sorting: ")
print(arr)
insertion_sort(arr, n);
print("Array after Sorting: ")
print(arr)

Array before Sorting: 
[67, 44, 82, 17, 20]
Array after Sorting: 
[17, 20, 44, 67, 82]

Kickstart Your Career

Get certified by completing the course

Get Started