Vertex Cover

Table of content

Vertex Cover

A vertex-cover of an undirected graph G = (V, E) is a subset of vertices V' ⊆ V such that if edge (u, v) is an edge of G, then either u in V or v in V' or both.

Find a vertex-cover of maximum size in a given undirected graph. This optimal vertexcover is the optimization version of an NP-complete problem. However, it is not too hard to find a vertex-cover that is near optimal.

APPROX-VERTEX_COVER (G: Graph) c ← { } E' ← E[G] 
while E' is not empty do 
   Let (u, v) be an arbitrary edge of E' c ← c U {u, v} 
   Remove from E' every edge incident on either u or v 
return c

Example

The set of edges of the given graph is −

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}

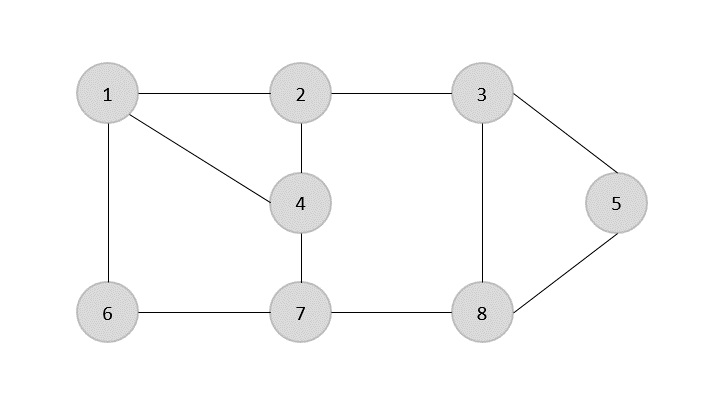
Set Edges

Now, we start by selecting an arbitrary edge (1,6). We eliminate all the edges, which are either incident to vertex 1 or 6 and we add edge (1,6) to cover.

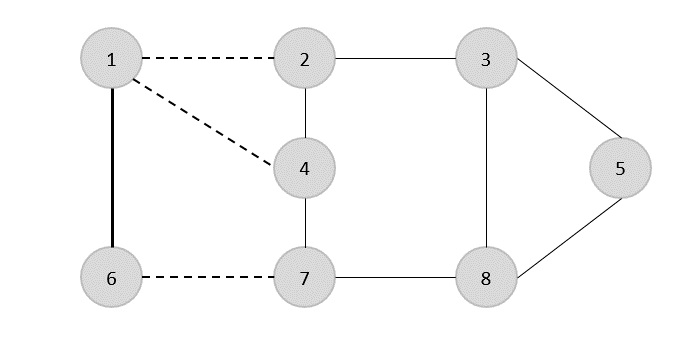
Arbitrary Edge

In the next step, we have chosen another edge (2,3) at random

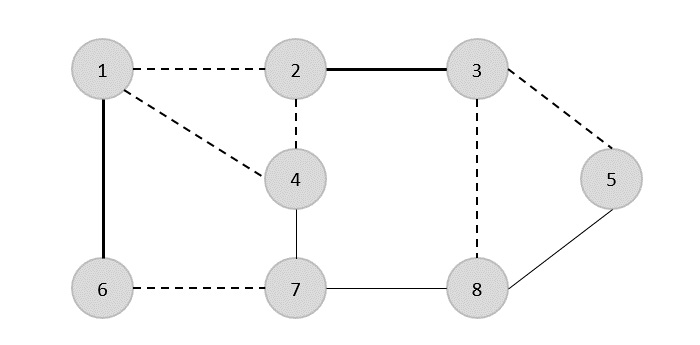
Another Edge

Now we select another edge (4,7).

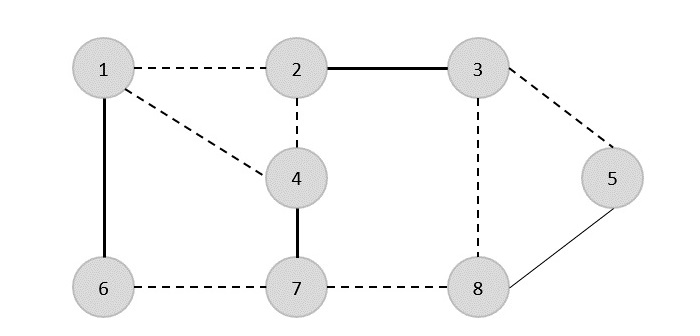
Select Another Edge

We select another edge (8,5).

Edge

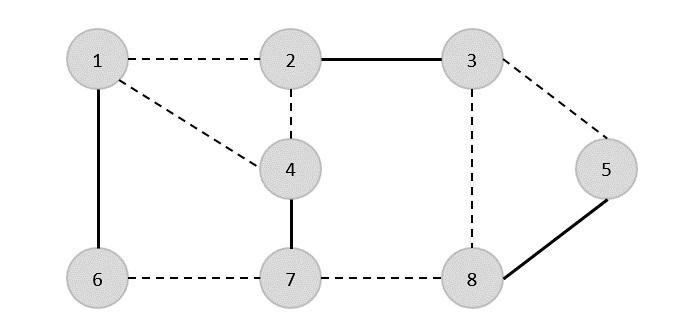
Hence, the vertex cover of this graph is {1,2,4,5}.

Analysis

It is easy to see that the running time of this algorithm is O(V + E), using adjacency list to represent E'.

Implementation

Following are the implementations of the above approach in various programming languages −

C C++ Java Python 
#include <stdio.h>
#include <stdbool.h>
#define MAX_VERTICES 100
int graph[MAX_VERTICES][MAX_VERTICES];
bool included[MAX_VERTICES];
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
   bool edgesRemaining[MAX_VERTICES][MAX_VERTICES];
   for (int i = 0; i < vertices; i++) {
      for (int j = 0; j < vertices; j++) {
         edgesRemaining[i][j] = graph[i][j];
      }
   }
   while (edges > 0) {
      int u, v;
      for (int i = 0; i < vertices; i++) {
         for (int j = 0; j < vertices; j++) {
            if (edgesRemaining[i][j]) {
               u = i;
               v = j;
               break;
            }
         }
      }
      included[u] = included[v] = true;
      for (int i = 0; i < vertices; i++) {
         edgesRemaining[u][i] = edgesRemaining[i][u] = false;
         edgesRemaining[v][i] = edgesRemaining[i][v] = false;
      }
      edges--;
   }
}
int main() {
   int vertices = 8;
   int edges = 10;
   int edgesData[10][2] = {{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
                           {6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
   for (int i = 0; i < edges; i++) {
      int u = edgesData[i][0];
      int v = edgesData[i][1];
      graph[u][v] = graph[v][u] = 1;
   }
   approxVertexCover(vertices, edges);
   printf("Vertex Cover: ");
   for (int i = 1; i <= vertices; i++) {
      if (included[i]) {
         printf("%d ", i);
      }
   }
   printf("\n");
   return 0;
}

Output

Vertex Cover: 1 3 4 5 6 7 

#include <iostream>
#include <vector>
using namespace std;
const int MAX_VERTICES = 100;
vector<vector<int>> graph(MAX_VERTICES, vector<int>(MAX_VERTICES, 0));
vector<bool> included(MAX_VERTICES, false);
// Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
void approxVertexCover(int vertices, int edges) {
   vector<vector<bool>> edgesRemaining(vertices, vector<bool>(vertices, false));
   for (int i = 0; i < vertices; i++) {
      for (int j = 0; j < vertices; j++) {
         edgesRemaining[i][j] = graph[i][j];
      }
   }
   while (edges > 0) {
      int u, v;
      for (int i = 0; i < vertices; i++) {
         for (int j = 0; j < vertices; j++) {
            if (edgesRemaining[i][j]) {
               u = i;
               v = j;
               break;
            }
         }
      }
      included[u] = included[v] = true;
      for (int i = 0; i < vertices; i++) {
         edgesRemaining[u][i] = edgesRemaining[i][u] = false;
         edgesRemaining[v][i] = edgesRemaining[i][v] = false;
      }
      edges--;
   }
}
int main() {
   int vertices = 8;
   int edges = 10;
   int edgesData[10][2] = {{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
                           {6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
   for (int i = 0; i < edges; i++) {
      int u = edgesData[i][0];
      int v = edgesData[i][1];
      graph[u][v] = graph[v][u] = 1;
   }
   approxVertexCover(vertices, edges);
   cout << "Vertex Cover: ";
   for (int i = 1; i <= vertices; i++) {
      if (included[i]) {
         cout << i << " ";
      }
   }
   cout << endl;
   return 0;
}

Output

Vertex Cover: 1 3 4 5 6 7 

import java.util.Arrays;
public class VertexCoverProblem {
   static final int MAX_VERTICES = 100;
   static int[][] graph = new int[MAX_VERTICES][MAX_VERTICES];
   static boolean[] included = new boolean[MAX_VERTICES];
   // Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
   static void approxVertexCover(int vertices, int edges) {
      int[][] edgesRemaining = new int[vertices][vertices];
      for (int i = 0; i < vertices; i++) {
         edgesRemaining[i] = Arrays.copyOf(graph[i], vertices);
      }
      while (edges > 0) {
         int u = -1, v = -1;
         for (int i = 0; i < vertices; i++) {
            for (int j = 0; j < vertices; j++) {
               if (edgesRemaining[i][j] == 1) {
                  u = i;
                  v = j;
                  break;
               }
            }
         }
         // Check if there are no more edges remaining
         if (u == -1 || v == -1) {
            break;
         }
         included[u] = included[v] = true;
         for (int i = 0; i < vertices; i++) {
            edgesRemaining[u][i] = edgesRemaining[i][u] = 0;
            edgesRemaining[v][i] = edgesRemaining[i][v] = 0;
         }
         edges--;
      }
   }
public static void main(String[] args) {
   int vertices = 8;
   int edges = 10;
   int[][] edgesData ={{1, 6}, {1, 2}, {1, 4}, {2, 3}, {2, 4},
                       {6, 7}, {4, 7}, {7, 8}, {3, 5}, {8, 5}};
   for (int i = 0; i < edges; i++) {
      int u = edgesData[i][0];
      int v = edgesData[i][1];
      graph[u][v] = graph[v][u] = 1;
   }
   approxVertexCover(vertices, edges);
   System.out.print("Vertex Cover: ");
   for (int i = 1; i <= vertices; i++) {
      if (included[i]) {
         System.out.print(i + " ");
      }
   }
   System.out.println();
   }
}

Output

Vertex Cover: 1 3 4 5 6 7 

MAX_VERTICES = 100
graph = [[0 for _ in range(MAX_VERTICES)] for _ in range(MAX_VERTICES)]
included = [False for _ in range(MAX_VERTICES)]
# Function to find Vertex Cover using the APPROX-VERTEX_COVER algorithm
def approx_vertex_cover(vertices, edges):
    edges_remaining = [row[:] for row in graph]
    while edges > 0:
        for i in range(vertices):
            for j in range(vertices):
                if edges_remaining[i][j]:
                    u = i
                    v = j
                    break
        included[u] = included[v] = True
        for i in range(vertices):
            edges_remaining[u][i] = edges_remaining[i][u] = False
            edges_remaining[v][i] = edges_remaining[i][v] = False
        edges -= 1
if __name__ == "__main__":
    vertices = 8
    edges = 10
    edges_data = [(1, 6), (1, 2), (1, 4), (2, 3), (2, 4),
                  (6, 7), (4, 7), (7, 8), (3, 5), (8, 5)]
    for u, v in edges_data:
        graph[u][v] = graph[v][u] = 1
    approx_vertex_cover(vertices, edges)
    print("Vertex Cover:", end=" ")
    for i in range(1, vertices + 1):
        if included[i]:
            print(i, end=" ")
    print()

Output

Vertex Cover: 1 3 4 5 6 7
Advertisements