
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
0-1 Knapsack Problem
We discussed the fractional knapsack problem using the greedy approach, earlier in this tutorial. It is shown that Greedy approach gives an optimal solution for Fractional Knapsack. However, this chapter will cover 0-1 Knapsack problem using dynamic programming approach and its analysis.
Unlike in fractional knapsack, the items are always stored fully without using the fractional part of them. Its either the item is added to the knapsack or not. That is why, this method is known as the 0-1 Knapsack problem.
Hence, in case of 0-1 Knapsack, the value of xi can be either 0 or 1, where other constraints remain the same.
0-1 Knapsack cannot be solved by Greedy approach. Greedy approach does not ensure an optimal solution in this method. In many instances, Greedy approach may give an optimal solution.
0-1 Knapsack Algorithm
Problem Statement − A thief is robbing a store and can carry a maximal weight of W into his knapsack. There are n items and weight of ith item is wi and the profit of selecting this item is pi. What items should the thief take?
Let i be the highest-numbered item in an optimal solution S for W dollars. Then S = S {i} is an optimal solution for W wi dollars and the value to the solution S is Vi plus the value of the sub-problem.
We can express this fact in the following formula: define c[i, w] to be the solution for items 1,2, , i and the maximum weight w.
The algorithm takes the following inputs
The maximum weight W
The number of items n
The two sequences v = <v1, v2, , vn> and w = <w1, w2, , wn>
The set of items to take can be deduced from the table, starting at c[n, w] and tracing backwards where the optimal values came from.
If c[i, w] = c[i-1, w], then item i is not part of the solution, and we continue tracing with c[i-1, w]. Otherwise, item i is part of the solution, and we continue tracing with c [i-1, w-W].
Dynamic-0-1-knapsack (v, w, n, W)
for w = 0 to W do
c[0, w] = 0
for i = 1 to n do
c[i, 0] = 0
for w = 1 to W do
if wi w then
if vi + c[i-1, w-wi] then
c[i, w] = vi + c[i-1, w-wi]
else c[i, w] = c[i-1, w]
else
c[i, w] = c[i-1, w]
The following examples will establish our statement.
Example
Let us consider that the capacity of the knapsack is W = 8 and the items are as shown in the following table.
| Item | A | B | C | D |
|---|---|---|---|---|
| Profit | 2 | 4 | 7 | 10 |
| Weight | 1 | 3 | 5 | 7 |
Solution
Using the greedy approach of 0-1 knapsack, the weight thats stored in the knapsack would be A+B = 4 with the maximum profit 2 + 4 = 6. But, that solution would not be the optimal solution.
Therefore, dynamic programming must be adopted to solve 0-1 knapsack problems.
Step 1
Construct an adjacency table with maximum weight of knapsack as rows and items with respective weights and profits as columns.
Values to be stored in the table are cumulative profits of the items whose weights do not exceed the maximum weight of the knapsack (designated values of each row)
So we add zeroes to the 0th row and 0th column because if the weight of item is 0, then it weighs nothing; if the maximum weight of knapsack is 0, then no item can be added into the knapsack.
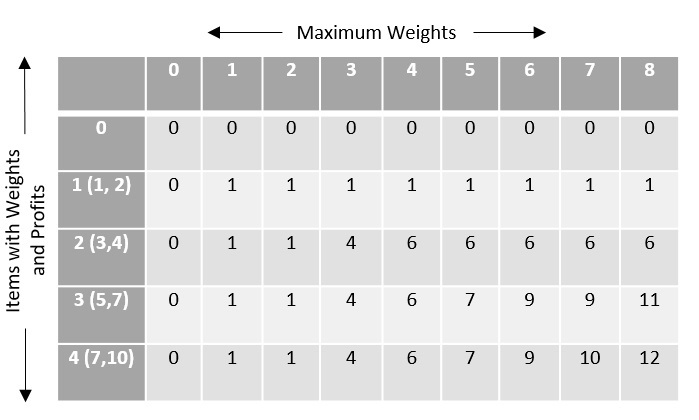
The remaining values are filled with the maximum profit achievable with respect to the items and weight per column that can be stored in the knapsack.
The formula to store the profit values is −
$$c\left [ i,w \right ]=max\left\{c\left [ i-1,w-w\left [ i \right ] \right ]+P\left [ i \right ] \right\}$$
By computing all the values using the formula, the table obtained would be −
To find the items to be added in the knapsack, recognize the maximum profit from the table and identify the items that make up the profit, in this example, its {1, 7}.
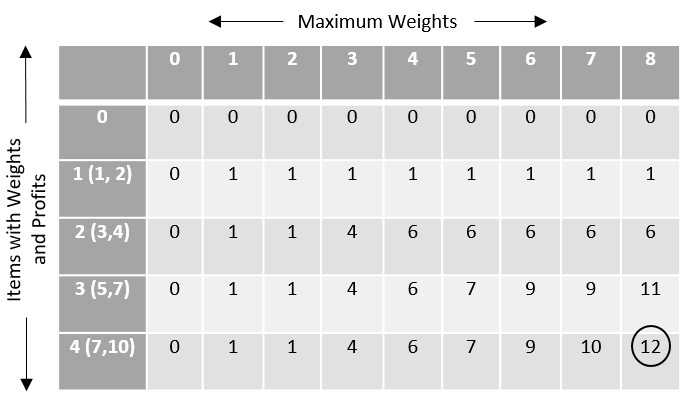
The optimal solution is {1, 7} with the maximum profit is 12.
Analysis
This algorithm takes (n.w) times as table c has (n+1).(w+1) entries, where each entry requires (1) time to compute.
Implementation
Following is the final implementation of 0-1 Knapsack Algorithm using Dynamic Programming Approach.
#include <stdio.h>
#include <string.h>
int findMax(int n1, int n2){
if(n1>n2) {
return n1;
} else {
return n2;
}
}
int knapsack(int W, int wt[], int val[], int n){
int K[n+1][W+1];
for(int i = 0; i<=n; i++) {
for(int w = 0; w<=W; w++) {
if(i == 0 || w == 0) {
K[i][w] = 0;
} else if(wt[i-1] <= w) {
K[i][w] = findMax(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w]);
} else {
K[i][w] = K[i-1][w];
}
}
}
return K[n][W];
}
int main(){
int val[5] = {70, 20, 50};
int wt[5] = {11, 12, 13};
int W = 30;
int len = sizeof val / sizeof val[0];
printf("Maximum Profit achieved with this knapsack: %d", knapsack(W, wt, val, len));
}
Output
Maximum Profit achieved with this knapsack: 120
#include <bits/stdc++.h>
using namespace std;
int max(int a, int b){
return (a > b) ? a : b;
}
int knapSack(int W, int wt[], int val[], int n){
int i, w;
vector<vector<int>> K(n + 1, vector<int>(W + 1));
for(i = 0; i <= n; i++) {
for(w = 0; w <= W; w++) {
if (i == 0 || w == 0)
K[i][w] = 0;
else if (wt[i - 1] <= w)
K[i][w] = max(val[i - 1] + K[i - 1][w - wt[i - 1]], K[i - 1][w]);
else
K[i][w] = K[i - 1][w];
}
}
return K[n][W];
}
int main(){
int val[] = { 70, 20, 50 };
int wt[] = { 11, 12, 13 };
int W = 30;
int n = sizeof(val) / sizeof(val[0]);
cout << "Maximum Profit achieved with this knapsack: " << knapSack(W, wt, val, n);
return 0;
}
Output
Maximum Profit achieved with this knapsack: 120
import java.util.*;
import java.lang.*;
public class Knapsack {
public static int findMax(int n1, int n2) {
if(n1>n2) {
return n1;
} else {
return n2;
}
}
public static int knapsack(int W, int wt[], int val[], int n) {
int K[][] = new int[n+1][W+1];
for(int i = 0; i<=n; i++) {
for(int w = 0; w<=W; w++) {
if(i == 0 || w == 0) {
K[i][w] = 0;
} else if(wt[i-1] <= w) {
K[i][w] = findMax(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w]);
} else {
K[i][w] = K[i-1][w];
}
}
}
return K[n][W];
}
public static void main(String[] args) {
int[] val = {70, 20, 50};
int[] wt = {11, 12, 13};
int W = 30;
int len = val.length;
System.out.print("Maximum Profit achieved with this knapsack: " + knapsack(W, wt, val, len));
}
}
Output
Maximum Profit achieved with this knapsack: 120
def knapsack(W, wt, val, n):
K = [[0] * (W+1) for i in range (n+1)]
for i in range(n+1):
for w in range(W+1):
if(i == 0 or w == 0):
K[i][w] = 0
elif(wt[i-1] <= w):
K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
else:
K[i][w] = K[i-1][w]
return K[n][W]
val = [70, 20, 50];
wt = [11, 12, 13];
W = 30;
ln = len(val);
profit = knapsack(W, wt, val, ln)
print("Maximum Profit achieved with this knapsack: ")
print(profit)
Output
Maximum Profit achieved with this knapsack: 120
