Insertion in Heaps

To insert an element in a heap, the new element is initially appended to the end of the heap as the last element of the array.

After inserting this element, heap property may be violated, hence the heap property is repaired by comparing the added element with its parent and moving the added element up a level, swapping positions with the parent. This process is called percolation up.

The comparison is repeated until the parent is larger than or equal to the percolating element.

Algorithm: Max-Heap-Insert (numbers[], key) 
heapsize = heapsize + 1 
numbers[heapsize] = -∞ 
i = heapsize 
numbers[i] = key 
while i > 1 and numbers[Parent(numbers[], i)] < numbers[i] 
   exchange(numbers[i], numbers[Parent(numbers[], i)]) 
   i = Parent (numbers[], i) 

Analysis

Initially, an element is being added at the end of the array. If it violates the heap property, the element is exchanged with its parent. The height of the tree is log n. Maximum log n number of operations needs to be performed.

Hence, the complexity of this function is O(log n).

Example

Let us consider a max-heap, as shown below, where a new element 5 needs to be added.

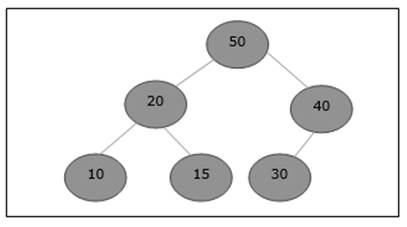
Initially, 55 will be added at the end of this array.

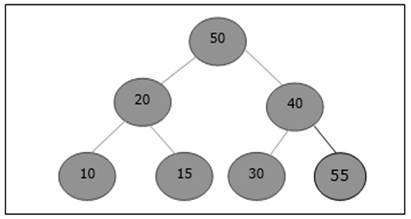
After insertion, it violates the heap property. Hence, the element needs to swap with its parent. After swap, the heap looks like the following.

Again, the element violates the property of heap. Hence, it is swapped with its parent.

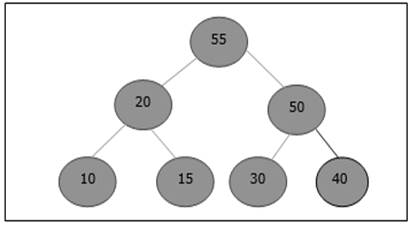
Now, we have to stop.

Example

Following are the implementations of this operation in various programming languages −

#include <stdio.h>
void swap(int* a, int* b) {
   int temp = *a;
   *a = *b;
   *b = temp;
}
int parent(int i) {
   if (i == 0)
      return -1;
   else
      return (i - 1) / 2;
}
void maxHeapInsert(int arr[], int* heapSize, int key) {
   (*heapSize)++;
   int i = *heapSize;
   arr[i] = key;
   while (i > 1 && arr[parent(i)] < arr[i]) {
      swap(&arr[i], &arr[parent(i)]);
      i = parent(i);
   }
}
int main() {
   int arr[100] = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
   int heapSize = 5; // Current heap size
   // New element to be inserted
   int newElement = 5;
   // Insert the new element into the Max-Heap
   maxHeapInsert(arr, &heapSize, newElement);
   // Print the updated Max-Heap
   printf("Updated Max-Heap: ");
   for (int i = 0; i <= heapSize; i++)
      printf("%d ", arr[i]);
   printf("\n");
   return 0;
}

Updated Max-Heap: 50 30 40 20 15 10 5 

#include <iostream>
#include <vector>
using namespace std;
void swap(int& a, int& b) {
   int temp = a;
   a = b;
   b = temp;
}
int parent(int i) {
   if (i == 0)
      return -1;
   else
      return (i - 1) / 2;
}
void maxHeapInsert(vector<int>& arr, int& heapSize, int key) {
   heapSize++;
   int i = heapSize;   
   // Resize the vector to accommodate the new element
   arr.push_back(0);
   arr[i] = key;
   while (i > 1 && arr[parent(i)] < arr[i]) {
      swap(arr[i], arr[parent(i)]);
      i = parent(i);
   }
}
int main() {
   vector<int> arr = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
   int heapSize = 5; // Current heap size
   // New element to be inserted
   int newElement = 5;
   // Insert the new element into the Max-Heap
   maxHeapInsert(arr, heapSize, newElement);
   // Print the updated Max-Heap
   cout << "Updated Max-Heap: ";
   for (int i = 0; i <= heapSize; i++)
      cout << arr[i] << " ";
   cout << endl;
   return 0;
}

Updated Max-Heap: 50 30 40 20 15 10 5

import java.util.Arrays;
public class MaxHeap {
   public static void swap(int arr[], int i, int j) {
      int temp = arr[i];
      arr[i] = arr[j];
      arr[j] = temp;
   }
   public static int parent(int i) {
      if (i == 0)
         return -1;
      else
         return (i - 1) / 2;
   }
   public static void maxHeapInsert(int arr[], int heapSize, int key) {
      heapSize++;
      int i = heapSize - 1; // Adjust the index for array insertion
      arr[i] = key;
      while (i > 0 && arr[parent(i)] < arr[i]) {
         swap(arr, i, parent(i));
         i = parent(i);
      }
   }
   public static void main(String args[]) {
      int arr[] = { 50, 30, 40, 20, 15, 10 }; // Initial Max-Heap
      int heapSize = 5; // Current heap size
      // New element to be inserted
      int newElement = 5;
      // Insert the new element into the Max-Heap
      maxHeapInsert(arr, heapSize, newElement);
      // Print the updated Max-Heap
      System.out.print("Updated Max-Heap: ");
      for (int i = 0; i <= heapSize; i++)
         System.out.print(arr[i] + " ");
      System.out.println();
   }
}

Updated Max-Heap: 50 30 40 20 15 5 

def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]
def parent(i):
    if i == 0:
        return -1
    else:
        return (i - 1) // 2
def max_heap_insert(arr, heap_size, key):
    heap_size += 1
    i = heap_size
    arr.append(key)
    while i > 0 and arr[parent(i)] < arr[i]:
        swap(arr, i, parent(i))
        i = parent(i)
if __name__ == "__main__":
    arr = [50, 30, 40, 20, 15, 10] # Initial Max-Heap
    heap_size = 5 # Current heap size
    # New element to be inserted
    new_element = 5
    # Insert the new element into the Max-Heap
    max_heap_insert(arr, heap_size, new_element)
    # Print the updated Max-Heap
    print("Updated Max-Heap:", arr)

Updated Max-Heap: [50, 30, 40, 20, 15, 10, 5]