Design and Analysis - Spanning Tree

A spanning tree is a subset of an undirected Graph that has all the vertices connected by minimum number of edges.

If all the vertices are connected in a graph, then there exists at least one spanning tree. In a graph, there may exist more than one spanning tree.

Properties

• A spanning tree does not have any cycle.

• Any vertex can be reached from any other vertex.

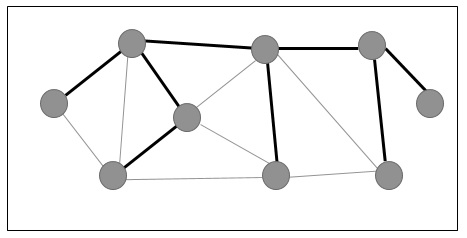
Example

In the following graph, the highlighted edges form a spanning tree.

Minimum Spanning Tree

A Minimum Spanning Tree (MST) is a subset of edges of a connected weighted undirected graph that connects all the vertices together with the minimum possible total edge weight. To derive an MST, Prim’s algorithm or Kruskal’s algorithm can be used. Hence, we will discuss Prim’s algorithm in this chapter.

As we have discussed, one graph may have more than one spanning tree. If there are n number of vertices, the spanning tree should have 𝒏−𝟏 number of edges. In this context, if each edge of the graph is associated with a weight and there exists more than one spanning tree, we need to find the minimum spanning tree of the graph.

Moreover, if there exist any duplicate weighted edges, the graph may have multiple minimum spanning tree.

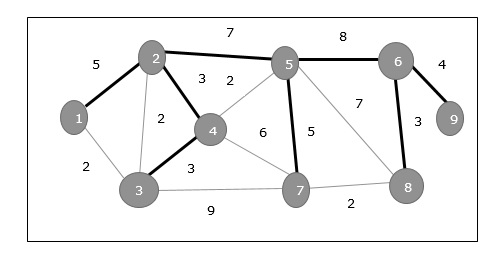
In the above graph, we have shown a spanning tree though it’s not the minimum spanning tree. The cost of this spanning tree is (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38.

We will use Prim’s algorithm to find the minimum spanning tree.

Prim’s Algorithm

Prim’s algorithm is a greedy approach to find the minimum spanning tree. In this algorithm, to form a MST we can start from an arbitrary vertex.

Algorithm: MST-Prim’s (G, w, r)
for each u є G.V
   u.key = ∞
   u.Π = NIL
r.key = 0
Q = G.V
while Q ≠ф
   u = Extract-Min (Q)
   for each v є G.adj[u]
      if each v є Q and w(u, v) <v.key
         v.Π = u
         v.key = w(u, v)

The function Extract-Min returns the vertex with minimum edge cost. This function works on min-heap.

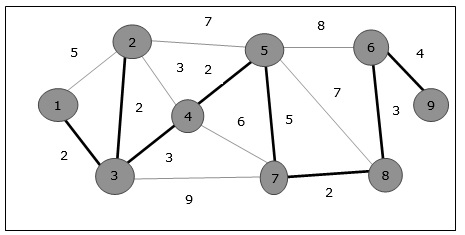
Example

Using Prim’s algorithm, we can start from any vertex, let us start from vertex 1.

Vertex 3 is connected to vertex 1 with minimum edge cost, hence edge (1, 2) is added to the spanning tree.

Next, edge (2, 3) is considered as this is the minimum among edges {(1, 2), (2, 3), (3, 4), (3, 7)}.

In the next step, we get edge (3, 4) and (2, 4) with minimum cost. Edge (3, 4) is selected at random.

In a similar way, edges (4, 5), (5, 7), (7, 8), (6, 8) and (6, 9) are selected. As all the vertices are visited, now the algorithm stops.

The cost of the spanning tree is (2 + 2 + 3 + 2 + 5 + 2 + 3 + 4) = 23 . There is no more spanning tree in this graph with cost less than 23.

Example

#include <stdio.h>
#include <stdbool.h>
#include <limits.h>
#define V 9
// Graph represented as an adjacency matrix with weights
int graph[V][V] = {
    {0, 5, 7, 3, 0, 0, 0, 0, 0},
    {5, 0, 8, 0, 7, 0, 0, 0, 0},
    {7, 8, 0, 3, 3, 3, 0, 0, 0},
    {3, 0, 3, 0, 0, 5, 0, 0, 0},
    {0, 7, 3, 0, 0, 0, 5, 0, 0},
    {0, 0, 3, 5, 0, 0, 8, 2, 0},
    {0, 0, 0, 0, 5, 8, 0, 3, 4},
    {0, 0, 0, 0, 0, 2, 3, 0, 3},
    {0, 0, 0, 0, 0, 0, 4, 3, 0}
};
// Helper function to extract the minimum key value from the set of vertices
int extractMin(int key[], bool mstSet[]) {
    int min = INT_MAX, min_index;
    for (int v = 0; v < V; v++)
        if (mstSet[v] == false && key[v] < min)
            min = key[v], min_index = v;
    return min_index;
}
// Function to find the Minimum Spanning Tree (MST) using Prim's algorithm
void primMST() {
    int parent[V];
    int key[V];
    bool mstSet[V];
    // Initialize key values and MST set
    for (int i = 0; i < V; i++) {
        key[i] = INT_MAX;
        mstSet[i] = false;
    }
    key[0] = 0; // Start with the first vertex (you can start from any vertex)
    parent[0] = -1; // First vertex is the root of MST
    // Find the MST
    for (int count = 0; count < V - 1; count++) {
        int u = extractMin(key, mstSet);
        mstSet[u] = true;
        for (int v = 0; v < V; v++) {
            // Update key value and parent index of adjacent vertices
            if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
                parent[v] = u;
                key[v] = graph[u][v];
            }
        }
    }
    // Print the MST and calculate the total cost
    int cost = 0;
    printf("Minimum Spanning Tree:\n");
    for (int i = 1; i < V; i++) {
        printf("Edge: (%d, %d), Weight: %d\n", parent[i], i, graph[i][parent[i]]);
        cost += graph[i][parent[i]];
    }
    printf("The cost of the spanning tree is: %d\n", cost);
}
int main() {
    primMST();
    return 0;
}

Minimum Spanning Tree:
Edge: (0, 1), Weight: 5
Edge: (3, 2), Weight: 3
Edge: (0, 3), Weight: 3
Edge: (2, 4), Weight: 3
Edge: (2, 5), Weight: 3
Edge: (7, 6), Weight: 3
Edge: (5, 7), Weight: 2
Edge: (7, 8), Weight: 3
The cost of the spanning tree is: 25

#include <iostream>
#include <vector>
#include <climits>
using namespace std;
#define V 9
// Graph represented as an adjacency matrix with weights
int graph[V][V] = {
    {0, 5, 7, 3, 0, 0, 0, 0, 0},
    {5, 0, 8, 0, 7, 0, 0, 0, 0},
    {7, 8, 0, 3, 3, 3, 0, 0, 0},
    {3, 0, 3, 0, 0, 5, 0, 0, 0},
    {0, 7, 3, 0, 0, 0, 5, 0, 0},
    {0, 0, 3, 5, 0, 0, 8, 2, 0},
    {0, 0, 0, 0, 5, 8, 0, 3, 4},
    {0, 0, 0, 0, 0, 2, 3, 0, 3},
    {0, 0, 0, 0, 0, 0, 4, 3, 0}
};
// Helper function to extract the minimum key value from the set of vertices
int extractMin(int key[], bool mstSet[]) {
    int min = INT_MAX, min_index = -1;
    for (int v = 0; v < V; v++) {
        if (mstSet[v] == false && key[v] < min) {
            min = key[v];
            min_index = v;
        }
    }
    return min_index;
}
// Function to find the Minimum Spanning Tree (MST) using Prim's algorithm
void primMST() {
    int parent[V];
    int key[V];
    bool mstSet[V];
    // Initialize key values and MST set
    for (int i = 0; i < V; i++) {
        key[i] = INT_MAX;
        mstSet[i] = false;
    }
    key[0] = 0; // Start with the first vertex (you can start from any vertex)
    parent[0] = -1; // First vertex is the root of MST
    // Find the MST
    for (int count = 0; count < V - 1; count++) {
        int u = extractMin(key, mstSet);
        mstSet[u] = true;
        for (int v = 0; v < V; v++) {
            // Update key value and parent index of adjacent vertices
            if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v]) {
                parent[v] = u;
                key[v] = graph[u][v];
            }
        }
    }
    // Print the MST and calculate the total cost
    int cost = 0;
    cout << "Minimum Spanning Tree:" << endl;
    for (int i = 1; i < V; i++) {
        cout << "Edge: (" << parent[i] << ", " << i << "), Weight: " << graph[i][parent[i]] << endl;
        cost += graph[i][parent[i]];
    }
    cout << "The cost of the spanning tree is: " << cost << endl;
}
int main() {
    primMST();
    return 0;
}

Minimum Spanning Tree:
Edge: (0, 1), Weight: 5
Edge: (3, 2), Weight: 3
Edge: (0, 3), Weight: 3
Edge: (2, 4), Weight: 3
Edge: (2, 5), Weight: 3
Edge: (7, 6), Weight: 3
Edge: (5, 7), Weight: 2
Edge: (7, 8), Weight: 3
The cost of the spanning tree is: 25

import java.util.Arrays;
class MSTPrimAlgorithm {
    private static final int V = 9;
    // Graph represented as an adjacency matrix with weights
    int graph[][] = {
        {0, 5, 7, 3, 0, 0, 0, 0, 0},
        {5, 0, 8, 0, 7, 0, 0, 0, 0},
        {7, 8, 0, 3, 3, 3, 0, 0, 0},
        {3, 0, 3, 0, 0, 5, 0, 0, 0},
        {0, 7, 3, 0, 0, 0, 5, 0, 0},
        {0, 0, 3, 5, 0, 0, 8, 2, 0},
        {0, 0, 0, 0, 5, 8, 0, 3, 4},
        {0, 0, 0, 0, 0, 2, 3, 0, 3},
        {0, 0, 0, 0, 0, 0, 4, 3, 0}
    };
    // Helper function to extract the minimum key value from the set of vertices
    int extractMin(int key[], boolean mstSet[]) {
        int min = Integer.MAX_VALUE, minIndex = -1;
        for (int v = 0; v < V; v++) {
            if (!mstSet[v] && key[v] < min) {
                min = key[v];
                minIndex = v;
            }
        }
        return minIndex;
    }
    // Function to find the Minimum Spanning Tree (MST) using Prim's algorithm
    void primMST() {
        int parent[] = new int[V];
        int key[] = new int[V];
        boolean mstSet[] = new boolean[V];
        Arrays.fill(key, Integer.MAX_VALUE);
        Arrays.fill(mstSet, false);
        key[0] = 0; // Start with the first vertex (you can start from any vertex)
        parent[0] = -1; // First vertex is the root of MST

        // Find the MST
        for (int count = 0; count < V - 1; count++) {
            int u = extractMin(key, mstSet);
            mstSet[u] = true;

            for (int v = 0; v < V; v++) {
                // Update key value and parent index of adjacent vertices
                if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
                    parent[v] = u;
                    key[v] = graph[u][v];
                }
            }
        }
        // Print the MST and calculate the total cost
        int cost = 0;
        System.out.println("Minimum Spanning Tree:");
        for (int i = 1; i < V; i++) {
            System.out.println("Edge: (" + parent[i] + ", " + i + "), Weight: " + graph[i][parent[i]]);
            cost += graph[i][parent[i]];
        }
        System.out.println("The cost of the spanning tree is: " + cost);
    }
}
public class Main {
    public static void main(String[] args) {
        MSTPrimAlgorithm mst = new MSTPrimAlgorithm();
        mst.primMST();
    }
}

Minimum Spanning Tree:
Edge: (0, 1), Weight: 5
Edge: (3, 2), Weight: 3
Edge: (0, 3), Weight: 3
Edge: (2, 4), Weight: 3
Edge: (2, 5), Weight: 3
Edge: (7, 6), Weight: 3
Edge: (5, 7), Weight: 2
Edge: (7, 8), Weight: 3
The cost of the spanning tree is: 25

def prim_mst(graph):
    vertices = len(graph)
    parent = [-1] * vertices
    key = [float('inf')] * vertices
    mst_set = [False] * vertices
    key[0] = 0  # Start with the first vertex (you can start from any vertex)
    parent[0] = -1  # First vertex is the root of MST
    for _ in range(vertices):
        u = extract_min_key(key, mst_set)
        mst_set[u] = True
        for v in range(vertices):
            # Update key value and parent index of adjacent vertices
            if graph[u][v] and not mst_set[v] and graph[u][v] < key[v]:
                parent[v] = u
                key[v] = graph[u][v]
    # Print the MST and calculate the total cost
    cost = 0
    print("Minimum Spanning Tree:")
    for i in range(1, vertices):
        print(f"Edge: ({parent[i]}, {i}), Weight: {graph[i][parent[i]]}")
        cost += graph[i][parent[i]]
    print("The cost of the spanning tree is:", cost)
def extract_min_key(key, mst_set):
    min_key = float('inf')
    min_index = 0
    for v in range(len(key)):
        if not mst_set[v] and key[v] < min_key:
            min_key = key[v]
            min_index = v
    return min_index
# Graph represented as an adjacency matrix with weights
graph = [
    [0, 5, 7, 3, 0, 0, 0, 0, 0],
    [5, 0, 8, 0, 7, 0, 0, 0, 0],
    [7, 8, 0, 3, 3, 3, 0, 0, 0],
    [3, 0, 3, 0, 0, 5, 0, 0, 0],
    [0, 7, 3, 0, 0, 0, 5, 0, 0],
    [0, 0, 3, 5, 0, 0, 8, 2, 0],
    [0, 0, 0, 0, 5, 8, 0, 3, 4],
    [0, 0, 0, 0, 0, 2, 3, 0, 3],
    [0, 0, 0, 0, 0, 0, 4, 3, 0]
]
prim_mst(graph)

Minimum Spanning Tree:
Edge: (0, 1), Weight: 5
Edge: (3, 2), Weight: 3
Edge: (0, 3), Weight: 3
Edge: (2, 4), Weight: 3
Edge: (2, 5), Weight: 3
Edge: (7, 6), Weight: 3
Edge: (5, 7), Weight: 2
Edge: (7, 8), Weight: 3
The cost of the spanning tree is: 25