Dynamic Programming

---

---

Dynamic programming approach is similar to divide and conquer in breaking down the problem into smaller and yet smaller possible sub-problems. But unlike divide and conquer, these sub-problems are not solved independently. Rather, results of these smaller sub-problems are remembered and used for similar or overlapping sub-problems.

Mostly, dynamic programming algorithms are used for solving optimization problems. Before solving the in-hand sub-problem, dynamic algorithm will try to examine the results of the previously solved sub-problems. The solutions of sub-problems are combined in order to achieve the best optimal final solution. This paradigm is thus said to be using Bottom-up approach.

So we can conclude that −

• The problem should be able to be divided into smaller overlapping sub-problem.

• Final optimum solution can be achieved by using an optimum solution of smaller sub-problems.

• Dynamic algorithms use memorization.

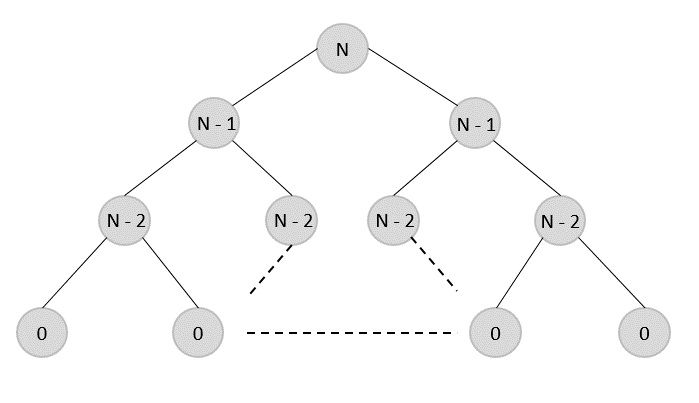
However, in a problem, two main properties can suggest that the given problem can be solved using Dynamic Programming. They are −

Overlapping Sub-Problems

Similar to Divide-and-Conquer approach, Dynamic Programming also combines solutions to sub-problems. It is mainly used where the solution of one sub-problem is needed repeatedly. The computed solutions are stored in a table, so that these don’t have to be re-computed. Hence, this technique is needed where overlapping sub-problem exists.

For example, Binary Search does not have overlapping sub-problem. Whereas recursive program of Fibonacci numbers have many overlapping sub-problems.

Optimal Sub-Structure

A given problem has Optimal Substructure Property, if the optimal solution of the given problem can be obtained using optimal solutions of its sub-problems.

For example, the Shortest Path problem has the following optimal substructure property −

If a node x lies in the shortest path from a source node u to destination node v, then the shortest path from u to v is the combination of the shortest path from u to x, and the shortest path from x to v.

The standard All Pair Shortest Path algorithms like Floyd-Warshall and Bellman-Ford are typical examples of Dynamic Programming.

Steps of Dynamic Programming Approach

Dynamic Programming algorithm is designed using the following four steps −

• Characterize the structure of an optimal solution.

• Recursively define the value of an optimal solution.

• Compute the value of an optimal solution, typically in a bottom-up fashion.

• Construct an optimal solution from the computed information.

Dynamic Programming vs. Greedy vs. Divide and Conquer

In contrast to greedy algorithms, where local optimization is addressed, dynamic algorithms are motivated for an overall optimization of the problem.

In contrast to divide and conquer algorithms, where solutions are combined to achieve an overall solution, dynamic algorithms use the output of a smaller sub-problem and then try to optimize a bigger sub-problem. Dynamic algorithms use memorization to remember the output of already solved sub-problems.

Examples of Dynamic Programming

The following computer problems can be solved using dynamic programming approach −

• Matrix Chain Multiplication

• Floyd Warshall Algorithm

• 0-1 Knapsack Problem

• Longest Common Subsequence Algorithm

• Travelling Salesman Problem (Dynamic Approach)

Dynamic programming can be used in both top-down and bottom-up manner. And of course, most of the times, referring to the previous solution output is cheaper than re-computing in terms of CPU cycles.