Max Cliques

In an undirected graph, a clique is a complete sub-graph of the given graph. Complete sub-graph means, all the vertices of this sub-graph is connected to all other vertices of this sub-graph.

The Max-Clique problem is the computational problem of finding maximum clique of the graph. Max clique is used in many real-world problems.

Let us consider a social networking application, where vertices represent peoples profile and the edges represent mutual acquaintance in a graph. In this graph, a clique represents a subset of people who all know each other.

To find a maximum clique, one can systematically inspect all subsets, but this sort of brute-force search is too time-consuming for networks comprising more than a few dozen vertices.

Max-Clique Algorithm

The algorithm to find the maximum clique of a graph is relatively simple. The steps to the procedure are given below −

Step 1: Take a graph as an input to the algorithm with a non-empty set of vertices and edges.

Step 2: Create an output set and add the edges into it if they form a clique of the graph.

Step 3: Repeat Step 2 iteratively until all the vertices of the graph are checked, and the list does not form a clique further.

Step 4: Then the output set is backtracked to check which clique has the maximum edges in it.

Pseudocode

Algorithm: Max-Clique (G, n, k)
S := 
for i = 1 to k do
   t := choice (1n) 
   if t  S then
      return failure
   S := S U t 
for all pairs (i, j) such that i  S and j  S and i  j do
   if (i, j) is not a edge of the graph then 
      return failure
return success

Analysis

Max-Clique problem is a non-deterministic algorithm. In this algorithm, first we try to determine a set of k distinct vertices and then we try to test whether these vertices form a complete graph.

There is no polynomial time deterministic algorithm to solve this problem. This problem is NP-Complete.

Example

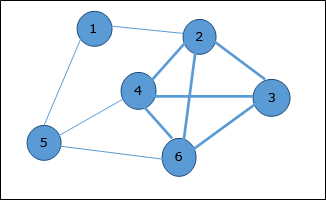
Take a look at the following graph. Here, the sub-graph containing vertices 2, 3, 4 and 6 forms a complete graph. Hence, this sub-graph is a clique. As this is the maximum complete sub-graph of the provided graph, its a 4-Clique.

Implementation

Following are the implementations of the above approach in various programming languages −

#include <stdio.h>
#define MAX 100
int store[MAX], n;
int graph[MAX][MAX];
int d[MAX];
int max(int a, int b){
   if(a > b){
      return a;
   }
   else{
      return b;
   }
}
int is_clique(int b)
{
   for (int i = 1; i < b; i++) {
      for (int j = i + 1; j < b; j++) {
         if (graph[store[i]][store[j]] == 0) {
            return 0;
         }
      }
   }
   return 1;
}
int maxCliques(int i, int l)
{
   int max_ = 0;
   for (int j = i + 1; j <= n; j++) {
      store[l] = j;
      if (is_clique(l + 1)) {
         max_ = max(max_, l);
         max_ = max(max_, maxCliques(j, l + 1));
      }
   }
   return max_;
}
int main()
{
   int edges[][2] = { { 1, 4 }, { 4, 6 }, { 1, 6 },
                      { 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = sizeof(edges) / sizeof(edges[0]);
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   printf("Max clique: %d\n", maxCliques(0, 1));
   return 0;
}

Max clique: 3

using namespace std;
#include<iostream>
const int MAX = 100;
// Storing the vertices
int store[MAX], n;
// Graph
int graph[MAX][MAX];
// Degree of the vertices
int d[MAX];
// Function to check if the given set of vertices in store array is a clique or not
bool is_clique(int b)
{
   // Run a loop for all set of edges
   for (int i = 1; i < b; i++) {
      for (int j = i + 1; j < b; j++)
   
      // If any edge is missing
      if (graph[store[i]][store[j]] == 0)
         return false;
   }
   return true;
}
// Function to find all the sizes of maximal cliques
int maxCliques(int i, int l)
{
   // Maximal clique size
   int max_ = 0;
   // Check if any vertices from i+1 can be inserted
   for (int j = i + 1; j <= n; j++) {
      // Add the vertex to store
      store[l] = j;
      // If the graph is not a clique of size k then
      // it cannot be a clique by adding another edge
      if (is_clique(l + 1)) {
   	     // Update max
   	     max_ = max(max_, l);
   	     // Check if another edge can be added
   	     max_ = max(max_, maxCliques(j, l + 1));
   	}
   }
   return max_;
}
// Driver code
int main()
{
   int edges[][2] = { { 1, 4 }, { 4, 6 }, { 1, 6 },
   				{ 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = sizeof(edges) / sizeof(edges[0]);
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   cout <<"Max clique: "<<maxCliques(0, 1);
   return 0;
}

Max clique: 3

import java.util.ArrayList;
import java.util.List;
public class MaxCliques {
   static final int MAX = 100;
   static int[] store = new int[MAX];
   static int[][] graph = new int[MAX][MAX];
   static int[] d = new int[MAX];
   static int n;
   // Function to check if the given set of vertices in store array is a clique or not
   static boolean isClique(int b) {
      for (int i = 1; i < b; i++) {
         for (int j = i + 1; j < b; j++)
            if (graph[store[i]][store[j]] == 0)
               return false;
      }
      return true;
   }
   // Function to find all the sizes of maximal cliques
   static int maxCliques(int i, int l) {
      int max_ = 0;
      for (int j = i + 1; j <= n; j++) {
         store[l] = j;
         if (isClique(l + 1)) {
            max_ = Math.max(max_, l);
            max_ = Math.max(max_, maxCliques(j, l + 1));
         }
      }
      return max_;
   }
   // Driver code
public static void main(String[] args) {
   int[][] edges = { { 1, 4 }, { 4, 6 }, { 1, 6 },
           { 3, 3 }, { 4, 2 }, { 8, 12 } };
   int size = edges.length;
   n = 6;
   for (int i = 0; i < size; i++) {
      graph[edges[i][0]][edges[i][1]] = 1;
      graph[edges[i][1]][edges[i][0]] = 1;
      d[edges[i][0]]++;
      d[edges[i][1]]++;
   }
   System.out.println("Max cliques: " + maxCliques(0, 1));
   }
}

Max cliques: 3

MAX = 100
# Storing the vertices
store = [0] * MAX
n = 0
# Graph
graph = [[0] * MAX for _ in range(MAX)]
# Degree of the vertices
d = [0] * MAX
# Function to check if the given set of vertices in store array is a clique or not
def is_clique(b):
    # Run a loop for all set of edges
    for i in range(1, b):
        for j in range(i + 1, b):
            # If any edge is missing
            if graph[store[i]][store[j]] == 0:
                return False
    return True
# Function to find all the sizes of maximal cliques
def maxCliques(i, l):
    # Maximal clique size
    max_ = 0
    # Check if any vertices from i+1 can be inserted
    for j in range(i + 1, n + 1):
        # Add the vertex to store
        store[l] = j
        # If the graph is not a clique of size k then
        # it cannot be a clique by adding another edge
        if is_clique(l + 1):
            # Update max
            max_ = max(max_, l)
            # Check if another edge can be added
            max_ = max(max_, maxCliques(j, l + 1))
    return max_
# Driver code
def main():
    global n
    edges = [(1, 4), (4, 6), (1, 6),
             (3, 3), (4, 2), (8, 12)]
    size = len(edges)
    n = 6
    for i in range(size):
        graph[edges[i][0]][edges[i][1]] = 1
        graph[edges[i][1]][edges[i][0]] = 1
        d[edges[i][0]] += 1
        d[edges[i][1]] += 1
    print("Max cliques:" ,maxCliques(0, 1))
if __name__ == "__main__":
    main()

Max cliques: 3