
- Network Theory Tutorial
- Network Theory - Home
- Network Theory - Overview
- Example Problems
- Network Theory - Active Elements
- Network Theory - Passive Elements
- Network Theory - Kirchhoff’s Laws
- Electrical Quantity Division Principles
- Network Theory - Nodal Analysis
- Network Theory - Mesh Analysis
- Network Theory - Equivalent Circuits
- Equivalent Circuits Example Problem
- Delta to Star Conversion
- Star to Delta Conversion
- Network Theory - Network Topology
- Network Topology Matrices
- Superposition Theorem
- Thevenin’s Theorem
- Network Theory - Norton’s Theorem
- Maximum Power Transfer Theorem
- Response of DC Circuits
- Response of AC Circuits
- Network Theory - Series Resonance
- Parallel Resonance
- Network Theory - Coupled Circuits
- Two-Port Networks
- Two-Port Parameter Conversions
- Network Theory - Filters
- Network Theory Useful Resources
- Network Theory - Quick Guide
- Network Theory - Useful Resources
- Network Theory - Discussion
Network Theory - Star to Delta Conversion
In the previous chapter, we discussed about the conversion of delta network into an equivalent star network. Now, let us discuss about the conversion of star network into an equivalent delta network. This conversion is called as Star to Delta Conversion.
In the previous chapter, we got the resistances of star network from delta network as
$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ Equation 1
$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ Equation 2
$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ Equation 3
Delta Network Resistances in terms of Star Network Resistances
Let us manipulate the above equations in order to get the resistances of delta network in terms of resistances of star network.
Multiply each set of two equations and then add.
$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$
$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$
$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ Equation 4
By dividing Equation 4 with Equation 2, we will get
$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$
$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
By dividing Equation 4 with Equation 3, we will get
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
By dividing Equation 4 with Equation 1, we will get
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
By using the above relations, we can find the resistances of delta network from the resistances of star network. In this way, we can convert star network into delta network.
Example
Let us calculate the resistances of delta network, which are equivalent to that of star network as shown in the following figure.
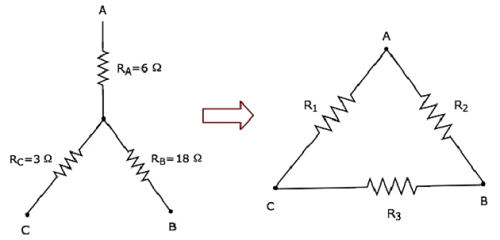
Given the resistances of star network as RA = 6 Ω, RB = 18 Ω and RC = 3 Ω.
We know the following relations of the resistances of delta network in terms of resistances of star network.
$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
Substitute the values of RA, RB and RC in the above equations.
$$R_1 = 3 + 6 + \frac{3 \times 6}{18} = 9 + 1 = 10 \Omega$$
$$R_2 = 6 + 18 + \frac{6 \times 18}{3} = 24 + 36 = 60 \Omega$$
$$R_3 = 18 + 3 + \frac{18 \times 3}{6} = 21 + 9 = 30 \Omega$$
So, we got the resistances of delta network as R1 = 10 Ω, R2 = 60 Ω and R3 = 30 Ω, which are equivalent to the resistances of the given star network.
To Continue Learning Please Login