
- Network Theory Tutorial
- Network Theory - Home
- Network Theory - Overview
- Example Problems
- Network Theory - Active Elements
- Network Theory - Passive Elements
- Network Theory - Kirchhoff’s Laws
- Electrical Quantity Division Principles
- Network Theory - Nodal Analysis
- Network Theory - Mesh Analysis
- Network Theory - Equivalent Circuits
- Equivalent Circuits Example Problem
- Delta to Star Conversion
- Star to Delta Conversion
- Network Theory - Network Topology
- Network Topology Matrices
- Superposition Theorem
- Thevenin’s Theorem
- Network Theory - Norton’s Theorem
- Maximum Power Transfer Theorem
- Response of DC Circuits
- Response of AC Circuits
- Network Theory - Series Resonance
- Parallel Resonance
- Network Theory - Coupled Circuits
- Two-Port Networks
- Two-Port Parameter Conversions
- Network Theory - Filters
- Network Theory Useful Resources
- Network Theory - Quick Guide
- Network Theory - Useful Resources
- Network Theory - Discussion
Network Theory - Thevenin’s Theorem
Thevenin’s theorem states that any two terminal linear network or circuit can be represented with an equivalent network or circuit, which consists of a voltage source in series with a resistor. It is known as Thevenin’s equivalent circuit. A linear circuit may contain independent sources, dependent sources, and resistors.
If the circuit contains multiple independent sources, dependent sources, and resistors, then the response in an element can be easily found by replacing the entire network to the left of that element with a Thevenin’s equivalent circuit.
The response in an element can be the voltage across that element, current flowing through that element, or power dissipated across that element.
This concept is illustrated in following figures.
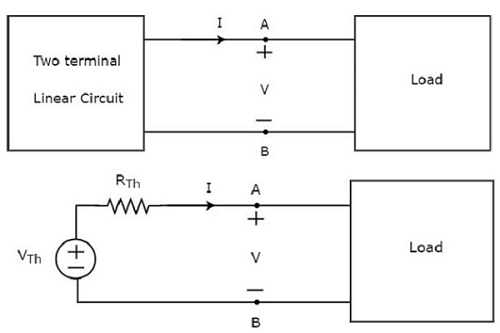
Thevenin’s equivalent circuit resembles a practical voltage source. Hence, it has a voltage source in series with a resistor.
The voltage source present in the Thevenin’s equivalent circuit is called as Thevenin’s equivalent voltage or simply Thevenin’s voltage, VTh.
The resistor present in the Thevenin’s equivalent circuit is called as Thevenin’s equivalent resistor or simply Thevenin’s resistor, RTh.
Methods of Finding Thevenin’s Equivalent Circuit
There are three methods for finding a Thevenin’s equivalent circuit. Based on the type of sources that are present in the network, we can choose one of these three methods. Now, let us discuss two methods one by one. We will discuss the third method in the next chapter.
Method 1
Follow these steps in order to find the Thevenin’s equivalent circuit, when only the sources of independent type are present.
Step 1 − Consider the circuit diagram by opening the terminals with respect to which the Thevenin’s equivalent circuit is to be found.
Step 2 − Find Thevenin’s voltage VTh across the open terminals of the above circuit.
Step 3 − Find Thevenin’s resistance RTh across the open terminals of the above circuit by eliminating the independent sources present in it.
Step 4 − Draw the Thevenin’s equivalent circuit by connecting a Thevenin’s voltage VTh in series with a Thevenin’s resistance RTh.
Now, we can find the response in an element that lies to the right side of Thevenin’s equivalent circuit.
Example
Find the current flowing through 20 Ω resistor by first finding a Thevenin’s equivalent circuit to the left of terminals A and B.
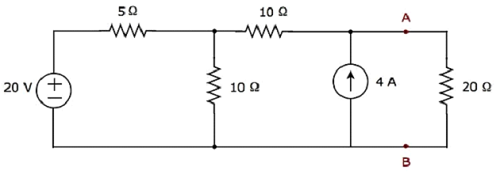
Step 1 − In order to find the Thevenin’s equivalent circuit to the left side of terminals A & B, we should remove the 20 Ω resistor from the network by opening the terminals A & B. The modified circuit diagram is shown in the following figure.
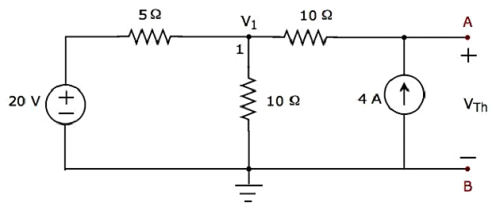
Step 2 − Calculation of Thevenin’s voltage VTh.
There is only one principal node except Ground in the above circuit. So, we can use nodal analysis method. The node voltage V1 and Thevenin’s voltage VTh are labelled in the above figure. Here, V1 is the voltage from node 1 with respect to Ground and VTh is the voltage across 4 A current source.
The nodal equation at node 1 is
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} - 4 = 0$$
$$\Rightarrow \frac{2V_1 - 40 + V_1 - 40}{10} = 0$$
$$\Rightarrow 3V_1 - 80 = 0$$
$$\Rightarrow V_1 = \frac{80}{3}V$$
The voltage across series branch 10 Ω resistor is
$$V_{10 \Omega} = (-4)(10) = -40V$$
There are two meshes in the above circuit. The KVL equation around second mesh is
$$V_1 - V_{10 \Omega} - V_{Th} = 0$$
Substitute the values of $V_1$ and $V_{10 \Omega}$ in the above equation.
$$\frac{80}{3} - (-40) - V_{Th} = 0$$
$$V_{Th} = \frac{80 + 120}{3} = \frac{200}{3}V$$
Therefore, the Thevenin’s voltage is $V_{Th} = \frac{200}{3}V$
Step 3 − Calculation of Thevenin’s resistance RTh.
Short circuit the voltage source and open circuit the current source of the above circuit in order to calculate the Thevenin’s resistance RTh across the terminals A & B. The modified circuit diagram is shown in the following figure.
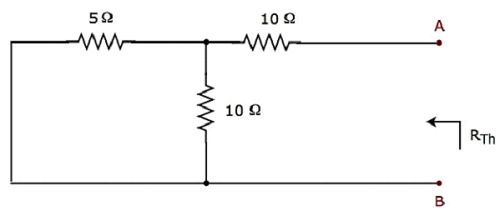
The Thevenin’s resistance across terminals A & B will be
$$R_{Th} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$
Therefore, the Thevenin’s resistance is $\mathbf {R_{Th} = \frac{40}{3} \Omega}$.
Step 4 − The Thevenin’s equivalent circuit is placed to the left of terminals A & B in the given circuit. This circuit diagram is shown in the following figure.
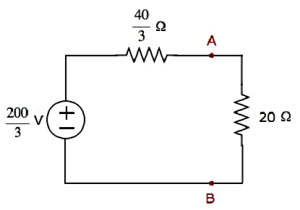
The current flowing through the 20 Ω resistor can be found by substituting the values of VTh, RTh and R in the following equation.
$$l = \frac{V_{Th}}{R_{Th} + R}$$
$$l = \frac{\frac{200}{3}}{\frac{40}{3} + 20} = \frac{200}{100} = 2A$$
Therefore, the current flowing through the 20 Ω resistor is 2 A.
Method 2
Follow these steps in order to find the Thevenin’s equivalent circuit, when the sources of both independent type and dependent type are present.
Step 1 − Consider the circuit diagram by opening the terminals with respect to which, the Thevenin’s equivalent circuit is to be found.
Step 2 − Find Thevenin’s voltage VTh across the open terminals of the above circuit.
Step 3 − Find the short circuit current ISC by shorting the two opened terminals of the above circuit.
Step 4 − Find Thevenin’s resistance RTh by using the following formula.
$$R_{Th} = \frac{V_{Th}}{I_{SC}}$$
Step 5 − Draw the Thevenin’s equivalent circuit by connecting a Thevenin’s voltage VTh in series with a Thevenin’s resistance RTh.
Now, we can find the response in an element that lies to the right side of the Thevenin’s equivalent circuit.