Digital Circuits - Threshold Logic

In previous chapters, we have implemented various combinational circuits using logic gates. Except NOT gate, the remaining all logic gates have at least two inputs and single output. Similarly, the threshold gate also contains at least one input and only one output.

Additionally, it contains the respective weights to each input and a threshold value. The values of these weights and threshold could be of any finite real number.

Basics of Threshold gate

Let the inputs of threshold gate are X1, X2, X3,ā€¦, Xn. The corresponding weights of these inputs are W1, W2, W3,ā€¦, Wn. The symbol of Threshold gate is shown in the following figure.

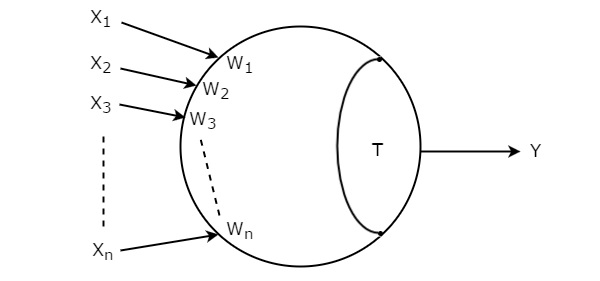
Basics Threshold Gate

Threshold gate is represented with a circle and it is having ā€˜nā€™ inputs, X1 to Xn and single output, Y. This circle is made into two parts. One part represents the weights corresponding to the inputs and other part represents Threshold value, T.

The sum of products of inputs with corresponding weights is known as weighted sum. If this weighted sum is greater than or equal to Threshold value, T then only the output, Y will be equal to one. Otherwise, the output, Y will be equal to zero.

Mathematically, we can write this relationship between inputs and output of Threshold gate as below.

$$Y=1, if \: \: W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}+...W_{n}X_{n}\geq T$$

š‘Œ = 0, otherwise.

Therefore, we can implement various logic gates and Boolean functions just by changing the values of weights and / or Threshold value, T.

Example

Let us find the simplified Boolean function for the following Threshold gate.

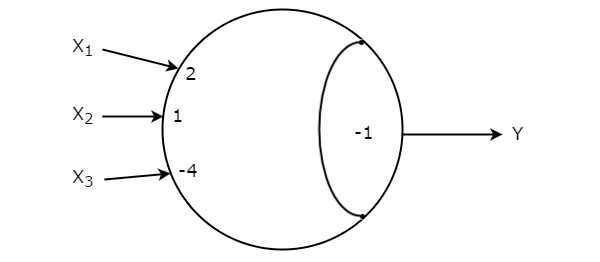
Threshold Gate Example

This Threshold gate is having three inputs X1, X2, X3 and one output Y.

The weights corresponding to the inputs X1, X2 & X3 are W1 = 2, W2 = 1 & W3 = -4 respectively.

The value of Threshold gate is T = -1.

The weighted sum of Threshold gate is

$$W=W_{1}X_{1}+W_{2}X_{2}+W_{3}X_{3}$$

Substitute the given weights in the above equation.

$$\Rightarrow W=2X_{1}+X_{2}-4X_{3}$$

Output of Threshold gate, Y will be ā€˜1ā€™ if W ≥ āˆ’1, otherwise it will be ā€˜0ā€™.

The following table shows the relationship between the input and output for all possible combination of inputs.

Inputs Weighted sum Output
$X_{1}$ $X_{2}$ $X_{3}$ $W=2X_{1}+X_{2}-4X_{3}$ $Y$
0 0 0 0 1
0 0 1 -4 0
0 1 0 1 1
0 1 1 -3 0
1 0 0 2 1
1 0 1 -2 0
1 1 0 3 1
1 1 1 -1 1

From the above table, we can write the Boolean function for output, Y as

$$Y= \sum m\left ( 0,2,4,6,7 \right )$$

The simplification of this Boolean function using 3 variable K-Map is shown in the following figure.

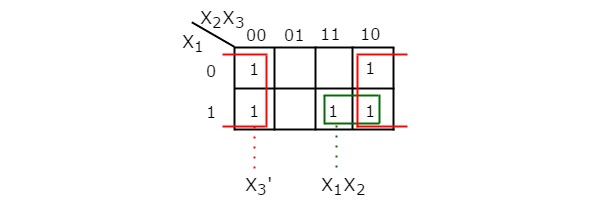
Simplified Boolean Function

Therefore, the simplified Boolean function for given Threshold gate is $Y={X_{3}'}+X_{1}X_{2}$.

Synthesis of Threshold Functions

Threshold gate is also called as universal gate because we can implement any Boolean function using Threshold gate(s). Some-times, it may not possible to implement few logic gates and Boolean functions by using single Threshold gate. In that case, we may require multiple Threshold gates.

Follow these steps for implementing a Boolean function using single Threshold gate.

Step 1 − Formulate a Truth table for given Boolean function.

Step 2 − In the above Truth table, add (include) one more column, which gives the relation between weighted sums and Threshold value.

Step 3 − Write the relation between weighted sums and threshold for each combination of inputs as mentioned below.

  • If the output of Boolean function is 1, then the weighted sum will be greater than or equal to Threshold value for those combination of inputs.

  • If the output of Boolean function is 0, then the weighted sum will be less than Threshold value for those combination of inputs.

Step 4 − Choose the values of weights & Threshold in such a way that they should satisfy all the relations present in last column of the above table.

step 5 − Draw the symbol of Threshold gate with those weights and Threshold value.

Example

Let us implement the following Boolean function using single Threshold gate.

$$Y\left ( X_{1},X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$$

The given Boolean function is a three variable function, which is represented in sum of min terms form. The Truth table of this function is shown below.

Inputs Output
X1 X2 X3 Y
0 0 0 1
0 0 1 0
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1

Now, let us add (include) one more column to the above Truth table. This last column contains the relations between weighted sums (W) and Threshold value (T) for each combination of inputs.

Inputs Output Relations between W & T
X1 X2 X3 Y
0 0 0 1 0 ≥T
0 0 1 0 W3 < T
0 1 0 1 W2 ≥ T
0 1 1 0 W2 + W3 < T
1 0 0 1 W1 ≥ T
1 0 1 0 W1+ W3 < T
1 1 0 1 W1+ W2 ≥ T
1 1 1 1 W1+ W2+ W3 ≥ T

Following are the conclusions from the above table.

  • The value of Threshold should be either zero or negative based on first relation.

  • The value of W3 should be negative based on first and second relations.

  • The values of W1 and W2 should be greater than or equal Threshold value based on fifth and third relations.

  • W2 should be greater than W3 based on fourth relation.

We can choose the following values for weights and Threshold based on the above conclusions.

W1=2, W2=1, W3= -4 & T = -1

The symbol of Threshold gate with the above values is shown below.

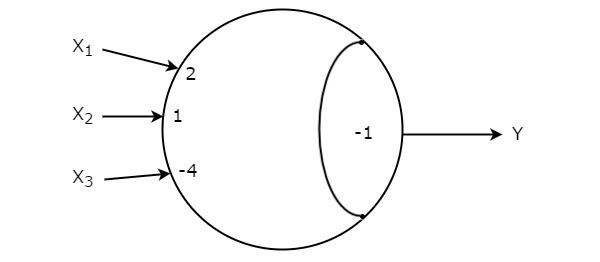
Symbol of Threshold Gate

Therefore, this Threshold gate implements the given Boolean function, $Y\left ( X_{1}, X_{2},X_{3} \right )=\sum m\left ( 0,2,4,6,7 \right )$.

Advertisements