
- Digital Circuits Tutorial
- Home
- Number Systems
- Base Conversions
- Binary Numbers Representation
- Signed Binary Arithmetic
- Codes
- Error Detection & Correction Codes
- Boolean Algebra
- Canonical and Standard Forms
- K-Map Method
- Quine-McCluskey Tabular Method
- Logic Gates
- Two-Level Logic Realization
- Combinational Circuits
- Arithmetic Circuits
- Decoders
- Encoders
- Multiplexers
- De-Multiplexers
- Programmable Logic Devices
- Threshold Logic
- Sequential Circuits
- Latches
- Flip-Flops
- Conversion of Flip-Flops
- Shift Registers
- Application of Shift Registers
- Counters
- Finite State Machines
- Algorithmic State Machine Charts
- Digital Circuits Resources
- Digital Circuits - Quick Guide
- Digital Circuits - Useful Resources
- Digital Circuits - Discussion
Digital Arithmetic Circuits
In this chapter, let us discuss about the basic arithmetic circuits like Binary adder and Binary subtractor. These circuits can be operated with binary values 0 and 1.
Binary Adder
The most basic arithmetic operation is addition. The circuit, which performs the addition of two binary numbers is known as Binary adder. First, let us implement an adder, which performs the addition of two bits.
Half Adder
Half adder is a combinational circuit, which performs the addition of two binary numbers A and B are of single bit. It produces two outputs sum, S & carry, C.
The Truth table of Half adder is shown below.
| Inputs | Outputs | ||
|---|---|---|---|
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
When we do the addition of two bits, the resultant sum can have the values ranging from 0 to 2 in decimal. We can represent the decimal digits 0 and 1 with single bit in binary. But, we can’t represent decimal digit 2 with single bit in binary. So, we require two bits for representing it in binary.
Let, sum, S is the Least significant bit and carry, C is the Most significant bit of the resultant sum. For first three combinations of inputs, carry, C is zero and the value of S will be either zero or one based on the number of ones present at the inputs. But, for last combination of inputs, carry, C is one and sum, S is zero, since the resultant sum is two.
From Truth table, we can directly write the Boolean functions for each output as
$$S=A \oplus B$$
$C=AB$
We can implement the above functions with 2-input Ex-OR gate & 2-input AND gate. The circuit diagram of Half adder is shown in the following figure.
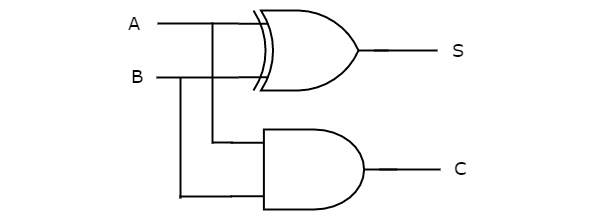
In the above circuit, a two input Ex-OR gate & two input AND gate produces sum, S & carry, C respectively. Therefore, Half-adder performs the addition of two bits.
Full Adder
Full adder is a combinational circuit, which performs the addition of three bits A, B and Cin. Where, A & B are the two parallel significant bits and Cin is the carry bit, which is generated from previous stage. This Full adder also produces two outputs sum, S & carry, Cout, which are similar to Half adder.
The Truth table of Full adder is shown below.
| Inputs | Outputs | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
When we do the addition of three bits, the resultant sum can have the values ranging from 0 to 3 in decimal. We can represent the decimal digits 0 and 1 with single bit in binary. But, we can’t represent the decimal digits 2 and 3 with single bit in binary. So, we require two bits for representing those two decimal digits in binary.
Let, sum, S is the Least significant bit and carry, Cout is the Most significant bit of resultant sum. It is easy to fill the values of outputs for all combinations of inputs in the truth table. Just count the number of ones present at the inputs and write the equivalent binary number at outputs. If Cin is equal to zero, then Full adder truth table is same as that of Half adder truth table.
We will get the following Boolean functions for each output after simplification.
$$S=A \oplus B \oplus C_{in}$$
$c_{out} = AB + \left ( A \oplus B \right )c_{in}$
The sum, S is equal to one, when odd number of ones present at the inputs. We know that Ex-OR gate produces an output, which is an odd function. So, we can use either two 2input Ex-OR gates or one 3-input Ex-OR gate in order to produce sum, S. We can implement carry, Cout using two 2-input AND gates & one OR gate. The circuit diagram of Full adder is shown in the following figure.
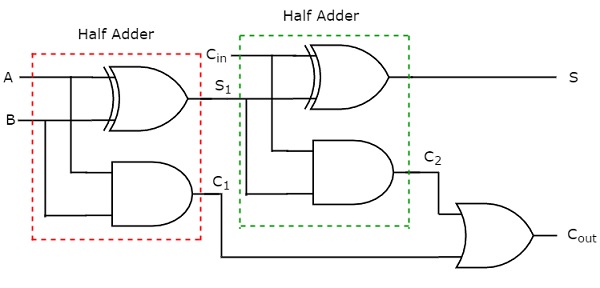
This adder is called as Full adder because for implementing one Full adder, we require two Half adders and one OR gate. If Cin is zero, then Full adder becomes Half adder. We can verify it easily from the above circuit diagram or from the Boolean functions of outputs of Full adder.
4-bit Binary Adder
The 4-bit binary adder performs the addition of two 4-bit numbers. Let the 4-bit binary numbers, $A=A_{3}A_{2}A_{1}A_{0}$ and $B= B_{3}B_{2}B_{1}B_{0}$. We can implement 4-bit binary adder in one of the two following ways.
Use one Half adder for doing the addition of two Least significant bits and three Full adders for doing the addition of three higher significant bits.
Use four Full adders for uniformity. Since, initial carry Cin is zero, the Full adder which is used for adding the least significant bits becomes Half adder.
For the time being, we considered second approach. The block diagram of 4-bit binary adder is shown in the following figure.
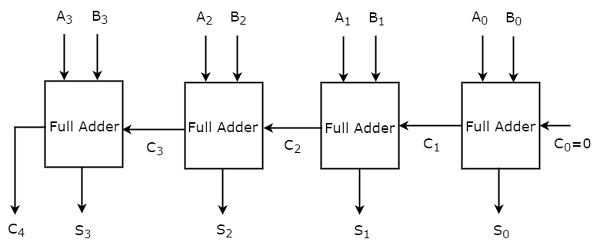
Here, the 4 Full adders are cascaded. Each Full adder is getting the respective bits of two parallel inputs A & B. The carry output of one Full adder will be the carry input of subsequent higher order Full adder. This 4-bit binary adder produces the resultant sum having at most 5 bits. So, carry out of last stage Full adder will be the MSB.
In this way, we can implement any higher order binary adder just by cascading the required number of Full adders. This binary adder is also called as ripple carry (binary) adder because the carry propagates (ripples) from one stage to the next stage.
Binary Subtractor
The circuit, which performs the subtraction of two binary numbers is known as Binary subtractor. We can implement Binary subtractor in following two methods.
- Cascade Full subtractors
- 2’s complement method
In first method, we will get an n-bit binary subtractor by cascading ‘n’ Full subtractors. So, first you can implement Half subtractor and Full subtractor, similar to Half adder & Full adder. Then, you can implement an n-bit binary subtractor, by cascading ‘n’ Full subtractors. So, we will be having two separate circuits for binary addition and subtraction of two binary numbers.
In second method, we can use same binary adder for subtracting two binary numbers just by doing some modifications in the second input. So, internally binary addition operation takes place but, the output is resultant subtraction.
We know that the subtraction of two binary numbers A & B can be written as,
$$A-B = A+\left ( {2}'s \: compliment \: of \: B \right )$$
$\Rightarrow A-B = A+\left ( {1}'s \: compliment \: of \: B \right )+1$
4-bit Binary Subtractor
The 4-bit binary subtractor produces the subtraction of two 4-bit numbers. Let the 4bit binary numbers, $A=A_{3}A_{2}A_{1}A_{0}$ and $B= B_{3}B_{2}B_{1}B_{0}$. Internally, the operation of 4-bit Binary subtractor is similar to that of 4-bit Binary adder. If the normal bits of binary number A, complemented bits of binary number B and initial carry (borrow), Cin as one are applied to 4-bit Binary adder, then it becomes 4-bit Binary subtractor. The block diagram of 4-bit binary subtractor is shown in the following figure.
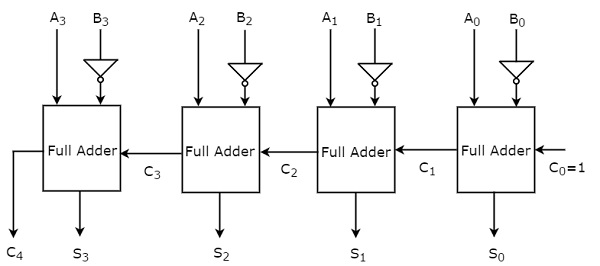
This 4-bit binary subtractor produces an output, which is having at most 5 bits. If Binary number A is greater than Binary number B, then MSB of the output is zero and the remaining bits hold the magnitude of A-B. If Binary number A is less than Binary number B, then MSB of the output is one. So, take the 2’s complement of output in order to get the magnitude of A-B.
In this way, we can implement any higher order binary subtractor just by cascading the required number of Full adders with necessary modifications.
Binary Adder / Subtractor
The circuit, which can be used to perform either addition or subtraction of two binary numbers at any time is known as Binary Adder / subtractor. Both, Binary adder and Binary subtractor contain a set of Full adders, which are cascaded. The input bits of binary number A are directly applied in both Binary adder and Binary subtractor.
There are two differences in the inputs of Full adders that are present in Binary adder and Binary subtractor.
The input bits of binary number B are directly applied to Full adders in Binary adder, whereas the complemented bits of binary number B are applied to Full adders in Binary subtractor.
The initial carry, C0 = 0 is applied in 4-bit Binary adder, whereas the initial carry (borrow), C0 = 1 is applied in 4-bit Binary subtractor.
We know that a 2-input Ex-OR gate produces an output, which is same as that of first input when other input is zero. Similarly, it produces an output, which is complement of first input when other input is one.
Therefore, we can apply the input bits of binary number B, to 2-input Ex-OR gates. The other input to all these Ex-OR gates is C0. So, based on the value of C0, the Ex-OR gates produce either the normal or complemented bits of binary number B.
4-bit Binary Adder / Subtractor
The 4-bit binary adder / subtractor produces either the addition or the subtraction of two 4-bit numbers based on the value of initial carry or borrow, 𝐶0. Let the 4-bit binary numbers, $A=A_{3}A_{2}A_{1}A_{0}$ and $B= B_{3}B_{2}B_{1}B_{0}$. The operation of 4-bit Binary adder / subtractor is similar to that of 4-bit Binary adder and 4-bit Binary subtractor.
Apply the normal bits of binary numbers A and B & initial carry or borrow, C0 from externally to a 4-bit binary adder. The block diagram of 4-bit binary adder / subtractor is shown in the following figure.
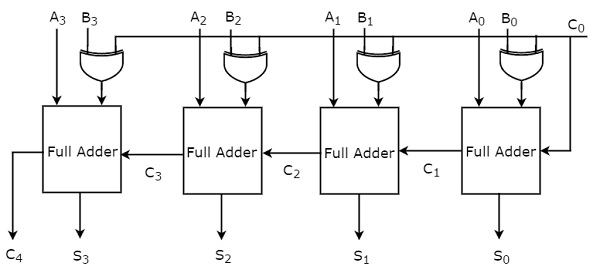
If initial carry, 𝐶0 is zero, then each full adder gets the normal bits of binary numbers A & B. So, the 4-bit binary adder / subtractor produces an output, which is the addition of two binary numbers A & B.
If initial borrow, 𝐶0 is one, then each full adder gets the normal bits of binary number A & complemented bits of binary number B. So, the 4-bit binary adder / subtractor produces an output, which is the subtraction of two binary numbers A & B.
Therefore, with the help of additional Ex-OR gates, the same circuit can be used for both addition and subtraction of two binary numbers.