
- Digital Circuits Tutorial
- Home
- Number Systems
- Base Conversions
- Binary Numbers Representation
- Signed Binary Arithmetic
- Codes
- Error Detection & Correction Codes
- Boolean Algebra
- Canonical and Standard Forms
- K-Map Method
- Quine-McCluskey Tabular Method
- Logic Gates
- Two-Level Logic Realization
- Combinational Circuits
- Arithmetic Circuits
- Decoders
- Encoders
- Multiplexers
- De-Multiplexers
- Programmable Logic Devices
- Threshold Logic
- Sequential Circuits
- Latches
- Flip-Flops
- Conversion of Flip-Flops
- Shift Registers
- Application of Shift Registers
- Counters
- Finite State Machines
- Algorithmic State Machine Charts
- Digital Circuits Resources
- Digital Circuits - Quick Guide
- Digital Circuits - Useful Resources
- Digital Circuits - Discussion
Digital Circuits - Logic Gates
Digital electronic circuits operate with voltages of two logic levelsnamely Logic Low and Logic High. The range of voltages corresponding to Logic Low is represented with ‘0’. Similarly, the range of voltages corresponding to Logic High is represented with ‘1’.
The basic digital electronic circuit that has one or more inputs and single output is known as Logic gate. Hence, the Logic gates are the building blocks of any digital system. We can classify these Logic gates into the following three categories.
- Basic gates
- Universal gates
- Special gates
Now, let us discuss about the Logic gates come under each category one by one.
Basic Gates
In earlier chapters, we learnt that the Boolean functions can be represented either in sum of products form or in product of sums form based on the requirement. So, we can implement these Boolean functions by using basic gates. The basic gates are AND, OR & NOT gates.
AND gate
An AND gate is a digital circuit that has two or more inputs and produces an output, which is the logical AND of all those inputs. It is optional to represent the Logical AND with the symbol ‘.’.
The following table shows the truth table of 2-input AND gate.
| A | B | Y = A.B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output of two input AND gate. If both inputs are ‘1’, then only the output, Y is ‘1’. For remaining combinations of inputs, the output, Y is ‘0’.
The following figure shows the symbol of an AND gate, which is having two inputs A, B and one output, Y.
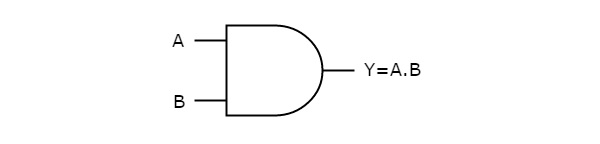
This AND gate produces an output (Y), which is the logical AND of two inputs A, B. Similarly, if there are ‘n’ inputs, then the AND gate produces an output, which is the logical AND of all those inputs. That means, the output of AND gate will be ‘1’, when all the inputs are ‘1’.
OR gate
An OR gate is a digital circuit that has two or more inputs and produces an output, which is the logical OR of all those inputs. This logical OR is represented with the symbol ‘+’.
The following table shows the truth table of 2-input OR gate.
| A | B | Y = A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output of two input OR gate. If both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.
The following figure shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.
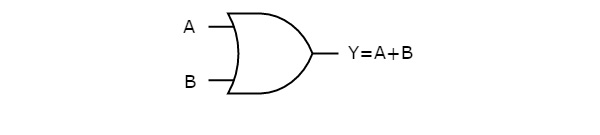
This OR gate produces an output (Y), which is the logical OR of two inputs A, B. Similarly, if there are ‘n’ inputs, then the OR gate produces an output, which is the logical OR of all those inputs. That means, the output of an OR gate will be ‘1’, when at least one of those inputs is ‘1’.
NOT gate
A NOT gate is a digital circuit that has single input and single output. The output of NOT gate is the logical inversion of input. Hence, the NOT gate is also called as inverter.
The following table shows the truth table of NOT gate.
| A | Y = A’ |
|---|---|
| 0 | 1 |
| 1 | 0 |
Here A and Y are the input and output of NOT gate respectively. If the input, A is ‘0’, then the output, Y is ‘1’. Similarly, if the input, A is ‘1’, then the output, Y is ‘0’.
The following figure shows the symbol of NOT gate, which is having one input, A and one output, Y.
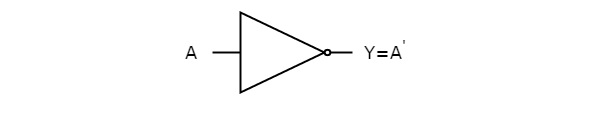
This NOT gate produces an output (Y), which is the complement of input, A.
Universal gates
NAND & NOR gates are called as universal gates. Because we can implement any Boolean function, which is in sum of products form by using NAND gates alone. Similarly, we can implement any Boolean function, which is in product of sums form by using NOR gates alone.
NAND gate
NAND gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical AND of all those inputs.
The following table shows the truth table of 2-input NAND gate.
| A | B | Y = (A.B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just opposite to that of two input AND gate operation.
The following image shows the symbol of NAND gate, which is having two inputs A, B and one output, Y.
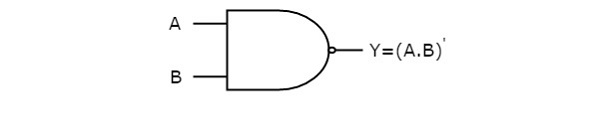
NAND gate operation is same as that of AND gate followed by an inverter. That’s why the NAND gate symbol is represented like that.
NOR gate
NOR gate is a digital circuit that has two or more inputs and produces an output, which is the inversion of logical OR of all those inputs.
The following table shows the truth table of 2-input NOR gate
| A | B | Y = (A+B)’ |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output. If both inputs are ‘0’, then the output, Y is ‘1’. If at least one of the input is ‘1’, then the output, Y is ‘0’. This is just opposite to that of two input OR gate operation.
The following figure shows the symbol of NOR gate, which is having two inputs A, B and one output, Y.
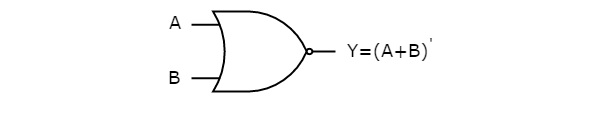
NOR gate operation is same as that of OR gate followed by an inverter. That’s why the NOR gate symbol is represented like that.
Special Gates
Ex-OR & Ex-NOR gates are called as special gates. Because, these two gates are special cases of OR & NOR gates.
Ex-OR gate
The full form of Ex-OR gate is Exclusive-OR gate. Its function is same as that of OR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-OR gate.
| A | B | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Here A, B are the inputs and Y is the output of two input Ex-OR gate. The truth table of Ex-OR gate is same as that of OR gate for first three rows. The only modification is in the fourth row. That means, the output (Y) is zero instead of one, when both the inputs are one, since the inputs having even number of ones.
Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.
Below figure shows the symbol of Ex-OR gate, which is having two inputs A, B and one output, Y.
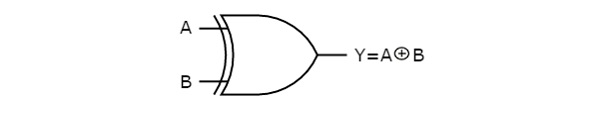
Ex-OR gate operation is similar to that of OR gate, except for few combination(s) of inputs. That’s why the Ex-OR gate symbol is represented like that. The output of Ex-OR gate is ‘1’, when odd number of ones present at the inputs. Hence, the output of Ex-OR gate is also called as an odd function.
Ex-NOR gate
The full form of Ex-NOR gate is Exclusive-NOR gate. Its function is same as that of NOR gate except for some cases, when the inputs having even number of ones.
The following table shows the truth table of 2-input Ex-NOR gate.
| A | B | Y = A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Here A, B are the inputs and Y is the output. The truth table of Ex-NOR gate is same as that of NOR gate for first three rows. The only modification is in the fourth row. That means, the output is one instead of zero, when both the inputs are one.
Therefore, the output of Ex-NOR gate is ‘1’, when both inputs are same. And it is zero, when both the inputs are different.
The following figure shows the symbol of Ex-NOR gate, which is having two inputs A, B and one output, Y.
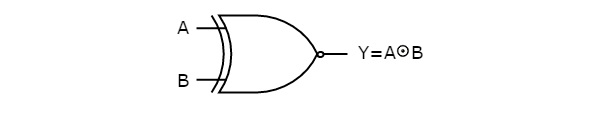
Ex-NOR gate operation is similar to that of NOR gate, except for few combination(s) of inputs. That’s why the Ex-NOR gate symbol is represented like that. The output of Ex-NOR gate is ‘1’, when even number of ones present at the inputs. Hence, the output of Ex-NOR gate is also called as an even function.
From the above truth tables of Ex-OR & Ex-NOR logic gates, we can easily notice that the Ex-NOR operation is just the logical inversion of Ex-OR operation.