
- Digital Circuits Tutorial
- Home
- Number Systems
- Base Conversions
- Binary Numbers Representation
- Signed Binary Arithmetic
- Codes
- Error Detection & Correction Codes
- Boolean Algebra
- Canonical and Standard Forms
- K-Map Method
- Quine-McCluskey Tabular Method
- Logic Gates
- Two-Level Logic Realization
- Combinational Circuits
- Arithmetic Circuits
- Decoders
- Encoders
- Multiplexers
- De-Multiplexers
- Programmable Logic Devices
- Threshold Logic
- Sequential Circuits
- Latches
- Flip-Flops
- Conversion of Flip-Flops
- Shift Registers
- Application of Shift Registers
- Counters
- Finite State Machines
- Algorithmic State Machine Charts
- Digital Circuits Resources
- Digital Circuits - Quick Guide
- Digital Circuits - Useful Resources
- Digital Circuits - Discussion
Digital Circuits - Finite State Machines
We know that synchronous sequential circuits change (affect) their states for every positive (or negative) transition of the clock signal based on the input. So, this behavior of synchronous sequential circuits can be represented in the graphical form and it is known as state diagram.
A synchronous sequential circuit is also called as Finite State Machine (FSM), if it has finite number of states. There are two types of FSMs.
- Mealy State Machine
- Moore State Machine
Now, let us discuss about these two state machines one by one.
Mealy State Machine
A Finite State Machine is said to be Mealy state machine, if outputs depend on both present inputs & present states. The block diagram of Mealy state machine is shown in the following figure.
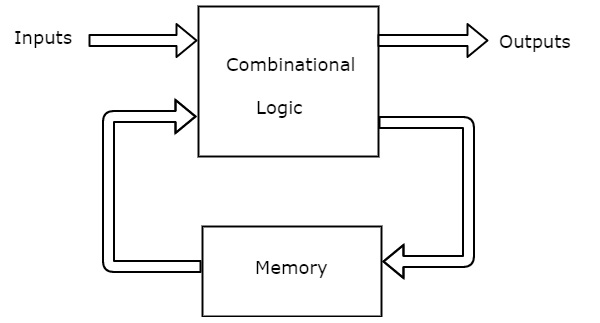
As shown in figure, there are two parts present in Mealy state machine. Those are combinational logic and memory. Memory is useful to provide some or part of previous outputs (present states) as inputs of combinational logic.
So, based on the present inputs and present states, the Mealy state machine produces outputs. Therefore, the outputs will be valid only at positive (or negative) transition of the clock signal.
The state diagram of Mealy state machine is shown in the following figure.
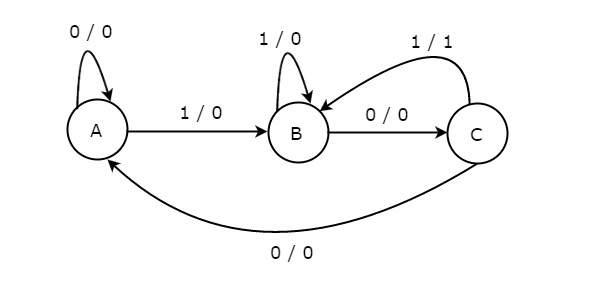
In the above figure, there are three states, namely A, B & C. These states are labelled inside the circles & each circle corresponds to one state. Transitions between these states are represented with directed lines. Here, 0 / 0, 1 / 0 & 1 / 1 denotes input / output. In the above figure, there are two transitions from each state based on the value of input, x.
In general, the number of states required in Mealy state machine is less than or equal to the number of states required in Moore state machine. There is an equivalent Moore state machine for each Mealy state machine.
Moore State Machine
A Finite State Machine is said to be Moore state machine, if outputs depend only on present states. The block diagram of Moore state machine is shown in the following figure.
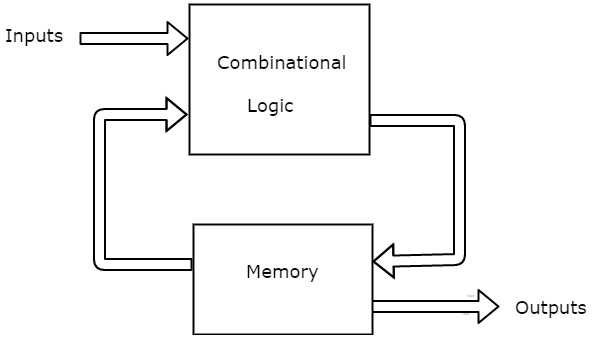
As shown in figure, there are two parts present in Moore state machine. Those are combinational logic and memory. In this case, the present inputs and present states determine the next states. So, based on next states, Moore state machine produces the outputs. Therefore, the outputs will be valid only after transition of the state.
The state diagram of Moore state machine is shown in the following figure.
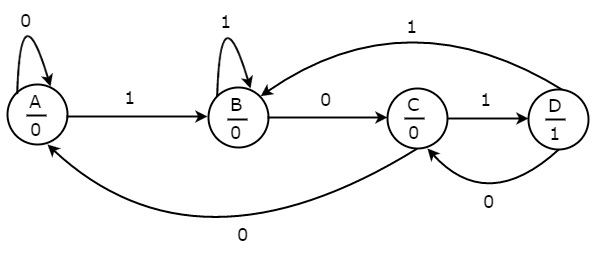
In the above figure, there are four states, namely A, B, C & D. These states and the respective outputs are labelled inside the circles. Here, only the input value is labeled on each transition. In the above figure, there are two transitions from each state based on the value of input, x.
In general, the number of states required in Moore state machine is more than or equal to the number of states required in Mealy state machine. There is an equivalent Mealy state machine for each Moore state machine. So, based on the requirement we can use one of them.