- Network Theory Tutorial
- Network Theory - Home
- Network Theory - Overview
- Example Problems
- Network Theory - Active Elements
- Network Theory - Passive Elements
- Network Theory - Kirchhoff’s Laws
- Electrical Quantity Division Principles
- Network Theory - Nodal Analysis
- Network Theory - Mesh Analysis
- Network Theory - Equivalent Circuits
- Equivalent Circuits Example Problem
- Delta to Star Conversion
- Star to Delta Conversion
- Network Theory - Network Topology
- Network Topology Matrices
- Superposition Theorem
- Thevenin’s Theorem
- Network Theory - Norton’s Theorem
- Maximum Power Transfer Theorem
- Response of DC Circuits
- Response of AC Circuits
- Network Theory - Series Resonance
- Parallel Resonance
- Network Theory - Coupled Circuits
- Two-Port Networks
- Two-Port Parameter Conversions
- Network Theory - Filters
- Network Theory Useful Resources
- Network Theory - Quick Guide
- Network Theory - Useful Resources
- Network Theory - Discussion
Network Theory - Mesh Analysis
In Mesh analysis, we will consider the currents flowing through each mesh. Hence, Mesh analysis is also called as Mesh-current method.
A branch is a path that joins two nodes and it contains a circuit element. If a branch belongs to only one mesh, then the branch current will be equal to mesh current.
If a branch is common to two meshes, then the branch current will be equal to the sum (or difference) of two mesh currents, when they are in same (or opposite) direction.
Procedure of Mesh Analysis
Follow these steps while solving any electrical network or circuit using Mesh analysis.
Step 1 − Identify the meshes and label the mesh currents in either clockwise or anti-clockwise direction.
Step 2 − Observe the amount of current that flows through each element in terms of mesh currents.
Step 3 − Write mesh equations to all meshes. Mesh equation is obtained by applying KVL first and then Ohm’s law.
Step 4 − Solve the mesh equations obtained in Step 3 in order to get the mesh currents.
Now, we can find the current flowing through any element and the voltage across any element that is present in the given network by using mesh currents.
Example
Find the voltage across 30 Ω resistor using Mesh analysis.
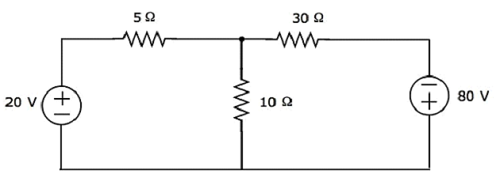
Step 1 − There are two meshes in the above circuit. The mesh currents I1 and I2 are considered in clockwise direction. These mesh currents are shown in the following figure.
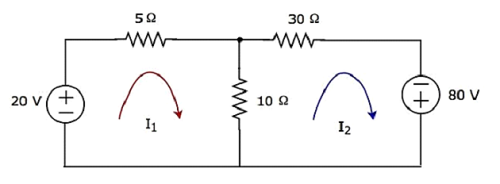
Step 2 − The mesh current I1 flows through 20 V voltage source and 5 Ω resistor. Similarly, the mesh current I2 flows through 30 Ω resistor and -80 V voltage source. But, the difference of two mesh currents, I1 and I2, flows through 10 Ω resistor, since it is the common branch of two meshes.
Step 3 − In this case, we will get two mesh equations since there are two meshes in the given circuit. When we write the mesh equations, assume the mesh current of that particular mesh as greater than all other mesh currents of the circuit.
The mesh equation of first mesh is
$$20 - 5I_1 -10(I_1 - I_2) = 0$$
$$\Rightarrow 20 - 15I_1 + 10I_2 = 0$$
$$\Rightarrow 10I_2 = 15I_1 - 20$$
Divide the above equation with 5.
$$2I_2 = 3I_1 - 4$$
Multiply the above equation with 2.
$4I_2 = 6I_1 - 8$ Equation 1
The mesh equation of second mesh is
$$-10(I_2 - I_1) - 30I_2 + 80 = 0$$
Divide the above equation with 10.
$$-(I_2 - I_1) - 3I_2 + 8 = 0$$
$$\Rightarrow -4I_2 + I_1 + 8 = 0$$
$4I_2 = I_1 + 8$ Equation 2
Step 4 − Finding mesh currents I1 and I2 by solving Equation 1 and Equation 2.
The left-hand side terms of Equation 1 and Equation 2 are the same. Hence, equate the right-hand side terms of Equation 1 and Equation 2 in order find the value of I1.
$$6I_1 - 8 = I_1 + 8$$
$$\Rightarrow 5I_1 = 16$$
$$\Rightarrow I_1 = \frac{16}{5} A$$
Substitute I1 value in Equation 2.
$$4I_2 = \frac{16}{5} + 8$$
$$\Rightarrow 4I_2 = \frac{56}{5}$$
$$\Rightarrow I_2 = \frac{14}{5} A$$
So, we got the mesh currents I1 and I2 as $\mathbf{\frac{16}{5}}$ A and $\mathbf{\frac{14}{5}}$ A respectively.
Step 5 − The current flowing through 30 Ω resistor is nothing but the mesh current I2 and it is equal to $\frac{14}{5}$ A. Now, we can find the voltage across 30 Ω resistor by using Ohm’s law.
$$V_{30 \Omega} = I_2 R$$
Substitute the values of I2 and R in the above equation.
$$V_{30 \Omega} = \lgroup \frac{14}{5} \rgroup 30$$
$$\Rightarrow V_{30 \Omega} = 84V$$
Therefore, the voltage across 30 Ω resistor of the given circuit is 84 V.
Note 1 − From the above example, we can conclude that we have to solve ‘m’ mesh equations, if the electric circuit is having ‘m’ meshes. That’s why we can choose Mesh analysis when the number of meshes is less than the number of principal nodes (except the reference node) of any electrical circuit.
Note 2 − We can choose either Nodal analysis or Mesh analysis, when the number of meshes is equal to the number of principal nodes (except the reference node) in any electric circuit.