
- Microwave Engineering - Home
- Introduction
- Transmission Lines
- Modes of Propagation
- Types of Transmission Lines
- Waveguides
- Components
- Avalanche Transit Time Devices
- Microwave Devices
- E-Plane Tee
- H-Plane Tee
- E-H Plane Tee
- Rat-race Junction
- Directional Couplers
- Cavity Klystron
- Reflex Klystron
- Travelling Wave Tube
- Magnetrons
- Measurement Devices
- Measurements
- Example Problems
Microwave Engineering - H-Plane Tee
An H-Plane Tee junction is formed by attaching a simple waveguide to a rectangular waveguide which already has two ports. The arms of rectangular waveguides make two ports called collinear ports i.e., Port1 and Port2, while the new one, Port3 is called as Side arm or H-arm. This H-plane Tee is also called as Shunt Tee.
As the axis of the side arm is parallel to the magnetic field, this junction is called H-Plane Tee junction. This is also called as Current junction, as the magnetic field divides itself into arms. The cross-sectional details of H-plane tee can be understood by the following figure.
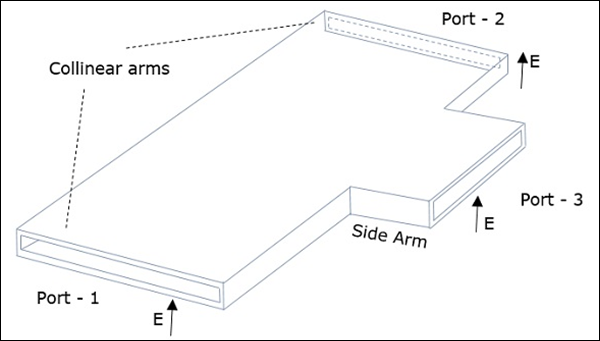
The following figure shows the connection made by the sidearm to the bi-directional waveguide to form the serial port.
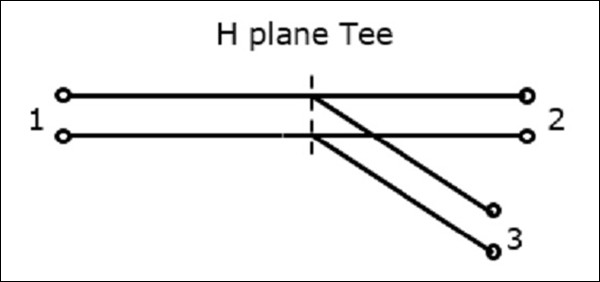
Properties of H-Plane Tee
The properties of H-Plane Tee can be defined by its $\left [ S \right ]_{3\times 3}$ matrix.
It is a 3×3 matrix as there are 3 possible inputs and 3 possible outputs.
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{21}& S_{22}& S_{23}\\ S_{31}& S_{32}& S_{33} \end{bmatrix}$ ........ Equation 1
Scattering coefficients $S_{13}$ and $S_{23}$ are equal here as the junction is symmetrical in plane.
From the symmetric property,
$S_{ij} = S_{ji}$
$S_{12} = S_{21} \: \: S_{23} = S_{32} = S_{13} \: \: S_{13} = S_{31}$
The port is perfectly matched
$S_{33} = 0$
Now, the $[S]$ matrix can be written as,
$[S] = \begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{12}& S_{22}& S_{13}\\ S_{13}& S_{13}& 0 \end{bmatrix}$ ........ Equation 2
We can say that we have four unknowns, considering the symmetry property.
From the Unitary property
$$[S][S]\ast = [I]$$
$$\begin{bmatrix} S_{11}& S_{12}& S_{13}\\ S_{12}& S_{22}& S_{13}\\ S_{13}& S_{13}& 0 \end{bmatrix} \: \begin{bmatrix} S_{11}^{*}& S_{12}^{*}& S_{13}^{*}\\ S_{12}^{*}& S_{22}^{*}& S_{13}^{*}\\ S_{13}^{*}& S_{13}^{*}& 0 \end{bmatrix} = \begin{bmatrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$
Multiplying we get,
(Noting R as row and C as column)
$R_1C_1 : S_{11}S_{11}^{*} + S_{12}S_{12}^{*} + S_{13}S_{13}^{*} = 1$
$\left | S_{11} \right |^2 + \left | S_{12} \right |^2 + \left | S_{13} \right |^2 = 1$ ........ Equation 3
$R_2C_2 : \left | S_{12} \right |^2 + \left | S_{22} \right |^2 + \left | S_{13} \right |^2 = 1$ ......... Equation 4
$R_3C_3 : \left | S_{13} \right |^2 + \left | S_{13} \right |^2 = 1$ ......... Equation 5
$R_3C_1 : S_{13}S_{11}^{*} - S_{13}S_{12}^{*} = 0$ ......... Equation 6
$2\left | S_{13} \right |^2 = 1 \quad or \quad S_{13} = \frac{1}{\sqrt{2}}$ ......... Equation 7
$\left | S_{11} \right |^2 = \left | S_{22} \right |^2$
$S_{11} = S_{22}$ ......... Equation 8
From the Equation 6,$S_{13}\left ( S_{11}^{*} + S_{12}^{*} \right ) = 0$
Since, $S_{13} \neq 0, S_{11}^{*} + S_{12}^{*} = 0, \: or \: S_{11}^{*} = -S_{12}^{*}$
Or $S_{11} = -S_{12} \:\: or \:\: S_{12} = -S_{11}$......... Equation 9
Using these in equation 3,
Since, $S_{13} \neq 0, S_{11}^{*} + S_{12}^{*} = 0, \: or \: S_{11}^{*} = -S_{12}^{*}$
$\left | S_{11} \right |^2 + \left | S_{11} \right |^2 + \frac{1}{2} = 1 \quad or \quad 2\left | S_{11} \right |^2 = \frac{1}{2} \quad or \quad S_{11} = \frac{1}{2}$..... Equation 10
From equation 8 and 9,
$S_{12} = -\frac{1}{2}$......... Equation 11
$S_{22} = \frac{1}{2}$......... Equation 12
Substituting for $S_{13}$, $S_{11}$, $S_{12}$ and $S_{22}$ from equation 7 and 10, 11 and 12 in equation 2,
We get,
$$\left [ S \right ] = \begin{bmatrix} \frac{1}{2}& -\frac{1}{2}& \frac{1}{\sqrt{2}}\\ -\frac{1}{2}& \frac{1}{2}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0 \end{bmatrix}$$
We know that $[b]$ = $[s] [a]$
$$\begin{bmatrix}b_1 \\ b_2 \\ b_3 \end{bmatrix} = \begin{bmatrix} \frac{1}{2}& -\frac{1}{2}& \frac{1}{\sqrt{2}}\\ -\frac{1}{2}& \frac{1}{2}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0 \end{bmatrix} \begin{bmatrix} a_1\\ a_2\\ a_3 \end{bmatrix}$$
This is the scattering matrix for H-Plane Tee, which explains its scattering properties.