
- Home
- Basics
- Python Ecosystem
- Methods for Machine Learning
- Data Loading for ML Projects
- Understanding Data with Statistics
- Understanding Data with Visualization
- Preparing Data
- Data Feature Selection
- ML Algorithms - Classification
- Introduction
- Logistic Regression
- Support Vector Machine (SVM)
- Decision Tree
- Naïve Bayes
- Random Forest
- ML Algorithms - Regression
- Random Forest
- Linear Regression
- ML Algorithms - Clustering
- Overview
- K-means Algorithm
- Mean Shift Algorithm
- Hierarchical Clustering
- ML Algorithms - KNN Algorithm
- Finding Nearest Neighbors
- Performance Metrics
- Automatic Workflows
- Improving Performance of ML Models
- Improving Performance of ML Model (Contd…)
- ML With Python - Resources
- Machine Learning With Python - Quick Guide
- Machine Learning with Python - Resources
- Machine Learning With Python - Discussion
Machine Learning with Python - Algorithms
Machine learning algorithms can be broadly classified into two types - Supervised and Unsupervised. This chapter discusses them in detail.
Supervised Learning
This algorithm consists of a target or outcome or dependent variable which is predicted from a given set of predictor or independent variables. Using these set of variables, we generate a function that maps input variables to desired output variables. The training process continues until the model achieves a desired level of accuracy on the training data.
Examples of Supervised Learning - Regression, Decision Tree, Random Forest, KNN, Logistic Regression etc.
Unsupervised Learning
In this algorithm, there is no target or outcome or dependent variable to predict or estimate. It is used for clustering a given data set into different groups, which is widely used for segmenting customers into different groups for specific intervention. Apriori algorithm and K-means are some of the examples of Unsupervised Learning.
Reinforcement Learning
Using this algorithm, the machine is trained to make specific decisions. Here, the algorithm trains itself continually by using trial and error methods and feedback methods. This machine learns from past experiences and tries to capture the best possible knowledge to make accurate business decisions.
Markov Decision Process is an example of Reinforcement Learning.
List of Common Machine Learning Algorithms
Here is the list of commonly used machine learning algorithms that can be applied to almost any data problem −
- Linear Regression
- Logistic Regression
- Decision Tree
- SVM
- Naive Bayes
- KNN
- K-Means
- Random Forest
- Dimensionality Reduction Algorithms
- Gradient Boosting algorithms like GBM, XGBoost, LightGBM and CatBoost
This section discusses each of them in detail −
Linear Regression
Linear regression is used to estimate real world values like cost of houses, number of calls, total sales etc. based on continuous variable(s). Here, we establish relationship between dependent and independent variables by fitting a best line. This line of best fit is known as regression line and is represented by the linear equation Y= a *X + b.
In this equation −
Y Dependent Variable
a Slope
X Independent variable
b Intercept
These coefficients a and b are derived based on minimizing the sum of squared difference of distance between data points and regression line.
Example
The best way to understand linear regression is by considering an example. Suppose we are asked to arrange students in a class in the increasing order of their weights. By looking at the students and visually analyzing their heights and builds we can arrange them as required using a combination of these parameters, namely height and build. This is real world linear regression example. We have figured out that height and build have correlation to the weight by a relationship, which looks similar to the equation above.
Types of Linear Regression
Linear Regression is of mainly two types - Simple Linear Regression and Multiple Linear Regression. Simple Linear Regression is characterized by one independent variable while Multiple Linear Regression is characterized by more than one independent variables. While finding the line of best fit, you can fit a polynomial or curvilinear regression. You can use the following code for this purpose.
import matplotlib.pyplot as plt plt.scatter(X, Y) yfit = [a + b * xi for xi in X] plt.plot(X, yfit)
Building a Linear Regressor
Regression is the process of estimating the relationship between input data and the continuous-valued output data. This data is usually in the form of real numbers, and our goal is to estimate the underlying function that governs the mapping from the input to the output.
Consider a mapping between input and output as shown −
1 --> 2 3 --> 6 4.3 --> 8.6 7.1 --> 14.2
You can easily estimate the relationship between the inputs and the outputs by analyzing the pattern. We can observe that the output is twice the input value in each case, hence the transformation would be − f(x) = 2x
Linear regression refers to estimating the relevant function using a linear combination of input variables. The preceding example was an example that consisted of one input variable and one output variable.
The goal of linear regression is to extract the relevant linear model that relates the input variable to the output variable. This aims to minimize the sum of squares of differences between the actual output and the predicted output using a linear function. This method is called Ordinary Least Squares. You may assume that a curvy line out there that fits these points better, but linear regression does not allow this. The main advantage of linear regression is that it is not complex. You may also find more accurate models in non-linear regression, but they will be slower. Here the model tries to approximate the input data points using a straight line.
Let us understand how to build a linear regression model in Python.
Consider that you have been provided with a data file, called data_singlevar.txt. This contains comma-separated lines where the first element is the input value and the second element is the output value that corresponds to this input value. You should use this as the input argument −
Assuming line of best fit for a set of points is −
y = a + b * x
where b = ( sum(xi * yi) - n * xbar * ybar ) / sum((xi - xbar)^2)
a = ybar - b * xbar
Use the following code for this purpose −
# sample points
X = [0, 6, 11, 14, 22]
Y = [1, 7, 12, 15, 21]
# solve for a and b
def best_fit(X, Y):
xbar = sum(X)/len(X)
ybar = sum(Y)/len(Y)
n = len(X) # or len(Y)
numer = sum([xi*yi for xi,yi in zip(X, Y)]) - n * xbar * ybar
denum = sum([xi**2 for xi in X]) - n * xbar**2
b = numer / denum
a = ybar - b * xbar
print('best fit line:\ny = {:.2f} + {:.2f}x'.format(a, b))
return a, b
# solution
a, b = best_fit(X, Y)
#best fit line:
#y = 0.80 + 0.92x
# plot points and fit line
import matplotlib.pyplot as plt
plt.scatter(X, Y)
yfit = [a + b * xi for xi in X]
plt.plot(X, yfit)
plt.show()
best fit line:
y = 1.48 + 0.92x
If you run the above code, you can observe the output graph as shown −
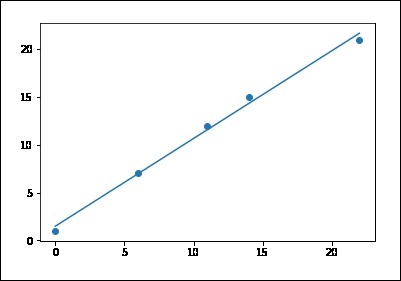
Note that this example uses only the first feature of the diabetes dataset, in order to illustrate a two-dimensional plot of this regression technique. The straight line can be seen in the plot, showing how linear regression attempts to draw a straight line that will best minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation.
You can calculate the coefficients, the residual sum of squares and the variance score using the program code shown below −
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis, 2]
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-30]
diabetes_X_test = diabetes_X[-30:]
# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-30]
diabetes_y_test = diabetes.target[-30:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean squared error
print("Mean squared error: %.2f"
% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color = 'black')
plt.plot(diabetes_X_test, diabetes_y_pred, color = 'blue', linewidth = 3)
plt.xticks(())
plt.yticks(())
plt.show()
You can observe the following output once you execute the code given above −
Automatically created module for IPython interactive environment
('Coefficients: \n', array([ 941.43097333]))
Mean squared error: 3035.06
Variance score: 0.41
Logistic Regression
Logistic regression is another technique borrowed by machine learning from statistics. It is the preferred method for binary classification problems, that is, problems with two class values.
It is a classification algorithm and not a regression algorithm as the name says. It is used to estimate discrete values or values like 0/1, Y/N, T/F based on the given set of independent variable(s). It predicts the probability of occurrence of an event by fitting data to a logit function. Hence, it is also called logit regression. Since, it predicts the probability, its output values lie between 0 and 1.
Example
Let us understand this algorithm through a simple example.
Assume that there is a puzzle to solve that has only 2 outcome scenarios either there is a solution or there is none. Now suppose, we have a wide range of puzzles to test a person which subjects he is good at. The outcomes may be something like this if a trigonometry puzzle is given, a person may be 80% likely to solve it. On the other hand, if a geography puzzle is given, the person may be only 20% likely to solve it. This is where Logistic Regression helps in solving. As per math, the log odds of the outcome is expressed as a linear combination of the predictor variables.
odds = p/ (1-p) = probability of event occurrence / probability of not event occurrence ln(odds) = ln(p/(1-p)) ; ln is the logarithm to the base e. logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
Note that in the above p is the probability of presence of the characteristic of interest. It chooses parameters that maximize the likelihood of observing the sample values rather than that minimize the sum of squared errors (like in ordinary regression).
Note that taking a log is one of the best mathematical way to replicate a step function.
The following points may be note-worthy when working on logistic regression −
It is similar to regression in that the objective is to find the values for the coefficients that weigh each input variable.
Unlike in linear regression, the prediction for the output is found using a non-linear function called the logistic function.
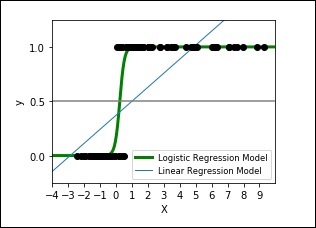
The logistic function appears like a big S and will change any value into the range 0 to 1. This is useful because we can apply a rule to the output of the logistic function to assign values to 0 and 1 and predict a class value.
The way the logistic regression model is learned, the predictions made by it can also be used as the probability of a given data instance belonging to class 0 or class 1. This can be useful for problems where you need to give more reasoning for a prediction.
Like linear regression, logistic regression works better when unrelated attributes of output variable are removed and similar attributes are removed.
The following code shows how to develop a plot for logistic expression where a synthetic dataset is classified into values as either 0 or 1, that is class one or two, using the logistic curve.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# This is the test set, it's a straight line with some Gaussian noise
xmin, xmax = -10, 10
n_samples = 100
np.random.seed(0)
X = np.random.normal(size = n_samples)
y = (X > 0).astype(np.float)
X[X > 0] *= 4
X += .3 * np.random.normal(size = n_samples)
X = X[:, np.newaxis]
# run the classifier
clf = linear_model.LogisticRegression(C=1e5)
clf.fit(X, y)
# and plot the result
plt.figure(1, figsize = (4, 3))
plt.clf()
plt.scatter(X.ravel(), y, color='black', zorder=20)
X_test = np.linspace(-10, 10, 300)
def model(x):
return 1 / (1 + np.exp(-x))
loss = model(X_test * clf.coef_ + clf.intercept_).ravel()
plt.plot(X_test, loss, color='blue', linewidth=3)
ols = linear_model.LinearRegression()
ols.fit(X, y)
plt.plot(X_test, ols.coef_ * X_test + ols.intercept_, linewidth=1)
plt.axhline(.5, color='.5')
plt.ylabel('y')
plt.xlabel('X')
plt.xticks(range(-10, 10))
plt.yticks([0, 0.5, 1])
plt.ylim(-.25, 1.25)
plt.xlim(-4, 10)
plt.legend(('Logistic Regression Model', 'Linear Regression Model'),
loc="lower right", fontsize='small')
plt.show()
The output plot will look like as shown here −
Decision Tree Algorithm
It is a supervised learning algorithm that is mostly used for classification problems. It works for both discrete and continuous dependent variables. In this algorithm, we split the population into two or more homogeneous sets. This is done based on most significant attributes to make as distinct groups as possible.
Decision trees are used widely in machine learning, covering both classification and regression. In decision analysis, a decision tree is used to visually and explicitly represent decisions and decision making. It uses a tree-like model of decisions.
A decision tree is drawn with its root at the top and branches at the bottom. In the image, the bold text represents a condition/internal node, based on which the tree splits into branches/ edges. The branch end that doesnt split anymore is the decision/leaf.
Example
Consider an example of using titanic data set for predicting whether a passenger will survive or not. The model below uses 3 features/attributes/columns from the data set, namely sex, age and sibsp (no of spouse/children). In this case, whether the passenger died or survived, is represented as red and green text respectively.
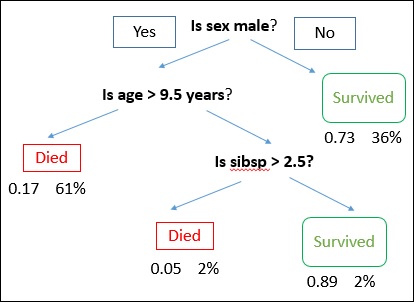
In some examples, we see that the population is classified into different groups based on multiple attributes to identify if they do something or not. To split the population into different heterogeneous groups, it uses various techniques like Gini, Information Gain, Chi-square, entropy etc.
The best way to understand how decision tree works, is to play Jezzball a classic game from Microsoft. Essentially, in this game, you have a room with moving walls and you need to create walls such that maximum area gets cleared off without the balls.
So, every time you split the room with a wall, you are trying to create 2 different populations with in the same room. Decision trees work in very similar fashion by dividing a population in as different groups as possible.
Observe the code and its output given below −
#Starting implementation
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
%matplotlib inline
from sklearn import tree
df = pd.read_csv("iris_df.csv")
df.columns = ["X1", "X2", "X3","X4", "Y"]
df.head()
#implementation
from sklearn.cross_validation import train_test_split
decision = tree.DecisionTreeClassifier(criterion="gini")
X = df.values[:, 0:4]
Y = df.values[:, 4]
trainX, testX, trainY, testY = train_test_split( X, Y, test_size = 0.3)
decision.fit(trainX, trainY)
print("Accuracy: \n", decision.score(testX, testY))
#Visualisation
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus as pydot
dot_data = StringIO()
tree.export_graphviz(decision, out_file=dot_data)
graph = pydot.graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png())
Output
Accuracy: 0.955555555556
Example
Here we are using the banknote authentication dataset to know the accuracy.
# Using the Bank Note dataset
from random import seed
from random import randrange
from csv import reader
# Loading a CSV file
filename ='data_banknote_authentication.csv'
def load_csv(filename):
file = open(filename, "rb")
lines = reader(file)
dataset = list(lines)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for i in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculating accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluating an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[-1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[-1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Splitting a dataset based on an attribute and an attribute value
def test_split(index, value, dataset):
left, right = list(), list()
for row in dataset:
if row[index] < value:
left.append(row)
else:
right.append(row)
return left, right
# Calculating the Gini index for a split dataset
def gini_index(groups, classes):
# count all samples at split point
n_instances = float(sum([len(group) for group in groups]))
# sum weighted Gini index for each group
gini = 0.0
for group in groups:
size = float(len(group))
# avoid divide by zero
if size == 0:
continue
score = 0.0
# score the group based on the score for each class
for class_val in classes:
p = [row[-1] for row in group].count(class_val) / size
score += p * p
# weight the group score by its relative size
gini += (1.0 - score) * (size / n_instances)
return gini
# Selecting the best split point for a dataset
def get_split(dataset):
class_values = list(set(row[-1] for row in dataset))
b_index, b_value, b_score, b_groups = 999, 999, 999, None
for index in range(len(dataset[0])-1):
for row in dataset:
groups = test_split(index, row[index], dataset)
gini = gini_index(groups, class_values)
if gini < b_score:
b_index, b_value, b_score, b_groups = index,
row[index], gini, groups
return {'index':b_index, 'value':b_value, 'groups':b_groups}
# Creating a terminal node value
def to_terminal(group):
outcomes = [row[-1] for row in group]
return max(set(outcomes), key=outcomes.count)
# Creating child splits for a node or make terminal
def split(node, max_depth, min_size, depth):
left, right = node['groups']
del(node['groups'])
# check for a no split
if not left or not right:
node['left'] = node['right'] = to_terminal(left + right)
return
# check for max depth
if depth >= max_depth:
node['left'], node['right'] = to_terminal(left), to_terminal(right)
return
# process left child
if len(left) <= min_size:
node['left'] = to_terminal(left)
else:
node['left'] = get_split(left)
split(node['left'], max_depth, min_size, depth+1)
# process right child
if len(right) <= min_size:
node['right'] = to_terminal(right)
else:
node['right'] = get_split(right)
split(node['right'], max_depth, min_size, depth+1)
# Building a decision tree
def build_tree(train, max_depth, min_size):
root = get_split(train)
split(root, max_depth, min_size, 1)
return root
# Making a prediction with a decision tree
def predict(node, row):
if row[node['index']] < node['value']:
if isinstance(node['left'], dict):
return predict(node['left'], row)
else:
return node['left']
else:
if isinstance(node['right'], dict):
return predict(node['right'], row)
else:
return node['right']
# Classification and Regression Tree Algorithm
def decision_tree(train, test, max_depth, min_size):
tree = build_tree(train, max_depth, min_size)
predictions = list()
for row in test:
prediction = predict(tree, row)
predictions.append(prediction)
return(predictions)
# Testing the Bank Note dataset
seed(1)
# load and prepare data
filename = 'data_banknote_authentication.csv'
dataset = load_csv(filename)
# convert string attributes to integers
for i in range(len(dataset[0])):
str_column_to_float(dataset, i)
# evaluate algorithm
n_folds = 5
max_depth = 5
min_size = 10
scores = evaluate_algorithm(dataset, decision_tree, n_folds, max_depth, min_size)
print('Scores: %s' % scores)
print('Mean Accuracy: %.3f%%' % (sum(scores)/float(len(scores))))
When you execute the code given above, you can observe the output as follows −
Scores: [95.62043795620438, 97.8102189781022, 97.8102189781022, 94.52554744525547, 98.90510948905109] Mean Accuracy: 96.934%
Support Vector Machines (SVM)
Support vector machines, also known as SVM, are well-known supervised classification algorithms that separate different categories of data.
These vectors are classified by optimizing the line so that the closest point in each of the groups will be the farthest away from each other.
This vector is by default linear and is also often visualized as being linear. However, the vector can also take a nonlinear form as well if the kernel type is changed from the default type of gaussian or linear.
It is a classification method, where we plot each data item as a point in n-dimensional space (where n is number of features) with the value of each feature being the value of a particular coordinate.
For example, if we have only two features like Height and Hair length of an individual, we should first plot these two variables in two dimensional space where each point has two co-ordinates known as Support Vectors. Observe the following diagram for better understanding −
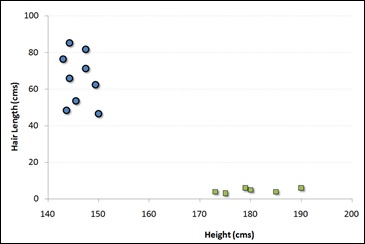
Now, find some line that splits the data between the two differently classified groups of data. This will be the line such that the distances from the closest point in each of the two groups will be farthest away.
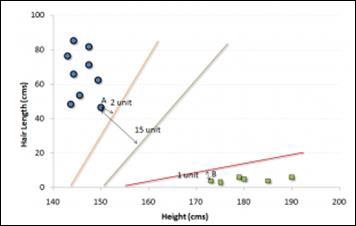
In the example shown above, the line which splits the data into two differently classified groups is the black line, since the two closest points are the farthest apart from the line. This line is our classifier. Then, depending on where the testing data lands on either side of the line, we can classify the new data.
from sklearn import svm
df = pd.read_csv('iris_df.csv')
df.columns = ['X4', 'X3', 'X1', 'X2', 'Y']
df = df.drop(['X4', 'X3'], 1)
df.head()
from sklearn.cross_validation import train_test_split
support = svm.SVC()
X = df.values[:, 0:2]
Y = df.values[:, 2]
trainX, testX, trainY, testY = train_test_split( X, Y, test_size = 0.3)
sns.set_context('notebook', font_scale=1.1)
sns.set_style('ticks')
sns.lmplot('X1','X2', scatter=True, fit_reg=False, data=df, hue='Y')
plt.ylabel('X2')
plt.xlabel('X1')
You can notice the following output and plot when you run the code shown above −
Text(0.5,27.256,'X1')
Nave Bayes Algorithm
It is a classification technique based on Bayes theorem with an assumption that predictor variables are independent. In simple words, a Naive Bayes classifier assumes that the presence of a particular feature in a class is not related to the presence of any other feature.
For example, a fruit may be considered to be an orange if it is orange in color, round, and about 3 inches in diameter. Even if these features are dependent on each other or upon the existence of the other features, a naive Bayes classifier would consider all of these characteristics to independently contribute to the probability that this fruit is an orange.
Naive Bayesian model is easy to make and particularly useful for very large data sets. Apart from being simple, Naive Bayes is known to outperform even highly advanced classification methods.
Bayes theorem provides a way of calculating posterior probability P(c|x) from P(c), P(x) and P(x|c). Observe the equation provided here: P(c/x) = P(x/c)P(c)/P(x)
where,
P(c|x) is the posterior probability of class (target) given predictor (attribute).
P(c) is the prior probability of class.
P(x|c) is the likelihood which is the probability of predictor given class.
P(x) is the prior probability of predictor.
Consider the example given below for a better understanding −
Assume a training data set of Weather and corresponding target variable Play. Now, we need to classify whether players will play or not based on weather condition. For this you will have to take the steps shown below −
Step 1 − Convert the data set to frequency table.
Step 2 − Create Likelihood table by finding the probabilities like Overcast probability = 0.29 and probability of playing is 0.64.
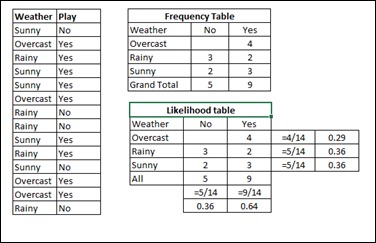
Step 3 − Now, use Naive Bayesian equation to calculate the posterior probability for each class. The class with the highest posterior probability is the outcome of prediction.
Problem − Players will play if weather is sunny, is this statement correct?
Solution − We can solve it using the method discussed above, so P(Yes | Sunny) = P( Sunny | Yes) * P(Yes) / P (Sunny)
Here we have, P (Sunny |Yes) = 3/9 = 0.33, P(Sunny) = 5/14 = 0.36, P(Yes) = 9/14 = 0.64
Now, P (Yes | Sunny) = 0.33 * 0.64 / 0.36 = 0.60, which has a higher probability.
Naive Bayes uses a similar method to predict the probability of different classes based on various attributes. This algorithm is mostly used in text classification and with problems having multiple classes.
The following code shows an example of Naive Bayes implementation −
import csv
import random
import math
def loadCsv(filename):
lines = csv.reader(open(filename, "rb"))
dataset = list(lines)
for i in range(len(dataset)):
dataset[i] = [float(x) for x in dataset[i]]
return dataset
def splitDataset(dataset, splitRatio):
trainSize = int(len(dataset) * splitRatio)
trainSet = []
copy = list(dataset)
while len(trainSet) < trainSize:
index = random.randrange(len(copy))
trainSet.append(copy.pop(index))
return [trainSet, copy]
def separateByClass(dataset):
separated = {}
for i in range(len(dataset)):
vector = dataset[i]
if (vector[-1] not in separated):
separated[vector[-1]] = []
separated[vector[-1]].append(vector)
return separated
def mean(numbers):
return sum(numbers)/float(len(numbers))
def stdev(numbers):
avg = mean(numbers)
variance = sum([pow(x-avg,2) for x in numbers])/float(len(numbers)-1)
return math.sqrt(variance)
def summarize(dataset):
summaries = [(mean(attribute), stdev(attribute)) for attribute in zip(*dataset)]
def summarizeByClass(dataset):
separated = separateByClass(dataset)
summaries = {}
for classValue, instances in separated.iteritems():
summaries[classValue] = summarize(instances)
return summaries
def calculateProbability(x, mean, stdev):
exponent = math.exp(-(math.pow(x-mean,2)/(2*math.pow(stdev,2))))
return (1 / (math.sqrt(2*math.pi) * stdev)) * exponent
def calculateClassProbabilities(summaries, inputVector):
probabilities = {}
for classValue, classSummaries in summaries.iteritems():
probabilities[classValue] = 1
for i in range(len(classSummaries)):
mean, stdev = classSummaries[i]
x = inputVector[i]
probabilities[classValue] *= calculateProbability(x, mean,stdev)
return probabilities
def predict(summaries, inputVector):
probabilities = calculateClassProbabilities(summaries, inputVector)
bestLabel, bestProb = None, -1
for classValue, probability in probabilities.iteritems():
if bestLabel is None or probability > bestProb:
bestProb = probability
bestLabel = classValue
return bestLabel
def getPredictions(summaries, testSet):
predictions = []
for i in range(len(testSet)):
result = predict(summaries, testSet[i])
predictions.append(result)
return predictions
def getAccuracy(testSet, predictions):
correct = 0
for i in range(len(testSet)):
if testSet[i][-1] == predictions[i]:
correct += 1
return (correct/float(len(testSet))) * 100.0
def main():
filename = 'pima-indians-diabetes.data.csv'
splitRatio = 0.67
dataset = loadCsv(filename)
trainingSet, testSet = splitDataset(dataset, splitRatio)
print('Split {0} rows into train = {1} and test = {2} rows').format(len(dataset), len(trainingSet), len(testSet))
# prepare model
summaries = summarizeByClass(trainingSet)
# test model
predictions = getPredictions(summaries, testSet)
accuracy = getAccuracy(testSet, predictions)
print('Accuracy: {0}%').format(accuracy)
main()
When you run the code given above, you can observe the following output −
Split 1372 rows into train = 919 and test = 453 rows Accuracy: 83.6644591611%
KNN (K-Nearest Neighbours)
K-Nearest Neighbors, KNN for short, is a supervised learning algorithm specialized in classification. It is a simple algorithm that stores all available cases and classifies new cases by a majority vote of its k neighbors. The case being assigned to the class is the most common among its K nearest neighbors measured by a distance function. These distance functions can be Euclidean, Manhattan, Minkowski and Hamming distance. First three functions are used for continuous function and fourth one (Hamming) for categorical variables. If K = 1, then the case is simply assigned to the class of its nearest neighbor. At times, choosing K turns out to be a challenge while performing KNN modeling.
The algorithm looks at different centroids and compares distance using some sort of function (usually Euclidean), then analyzes those results and assigns each point to the group so that it is optimized to be placed with all the closest points to it.
You can use KNN for both classification and regression problems. However, it is more widely used in classification problems in the industry. KNN can easily be mapped to our real lives.
You will have to note the following points before selecting KNN −
KNN is computationally expensive.
Variables should be normalized else higher range variables can bias it.
Works on pre-processing stage more before going for KNN like outlier, noise removal
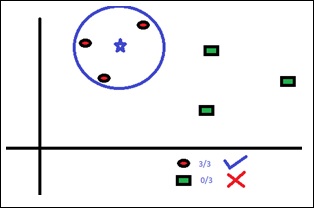
Observe the following code for a better understanding of KNN −
#Importing Libraries
from sklearn.neighbors import KNeighborsClassifier
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create KNeighbors classifier object model
KNeighborsClassifier(n_neighbors=6) # default value for n_neighbors is 5
# Train the model using the training sets and check score
model.fit(X, y)
#Predict Output
predicted= model.predict(x_test)
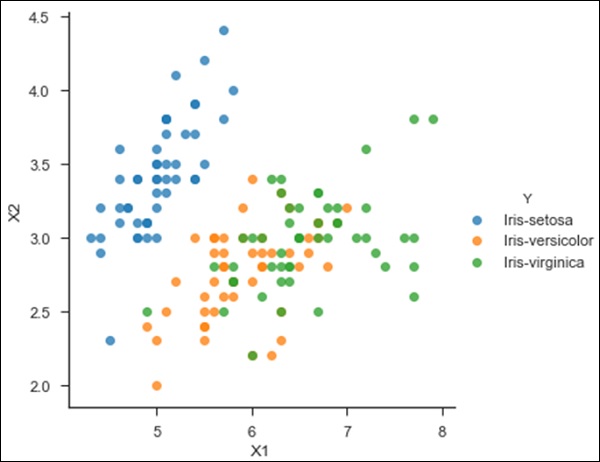
from sklearn.neighbors import KNeighborsClassifier
df = pd.read_csv('iris_df.csv')
df.columns = ['X1', 'X2', 'X3', 'X4', 'Y']
df = df.drop(['X4', 'X3'], 1)
df.head()
sns.set_context('notebook', font_scale=1.1)
sns.set_style('ticks')
sns.lmplot('X1','X2', scatter=True, fit_reg=False, data=df, hue='Y')
plt.ylabel('X2')
plt.xlabel('X1')
from sklearn.cross_validation import train_test_split
neighbors = KNeighborsClassifier(n_neighbors=5)
X = df.values[:, 0:2]
Y = df.values[:, 2]
trainX, testX, trainY, testY = train_test_split( X, Y, test_size = 0.3)
neighbors.fit(trainX, trainY)
print('Accuracy: \n', neighbors.score(testX, testY))
pred = neighbors.predict(testX)
The code given above will produce the following output −
('Accuracy: \n', 0.75555555555555554)
K-Means
It is a type of unsupervised algorithm which deals with the clustering problems. Its procedure follows a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters). Data points inside a cluster are homogeneous and are heterogeneous to peer groups.
How K-means Forms Cluster
K-means forms cluster in the steps given below −
K-means picks k number of points for each cluster known as centroids.
Each data point forms a cluster with the closest centroids, that is k clusters.
Finds the centroid of each cluster based on existing cluster members. Here we have new centroids.
As we have new centroids, repeat step 2 and 3. Find the closest distance for each data point from new centroids and get associated with new k-clusters. Repeat this process until convergence occurs, that is till centroids do not change.
Determination of Value of K
In K-means, we have clusters and each cluster has its own centroid. Sum of square of difference between centroid and the data points within a cluster constitutes the sum of square value for that cluster. Also, when the sum of square values for all the clusters are added, it becomes total within sum of square value for the cluster solution.
We know that as the number of cluster increases, this value keeps on decreasing but if you plot the result you may see that the sum of squared distance decreases sharply up to some value of k, and then much more slowly after that. Here, we can find the optimum number of cluster.
Observe the following code −
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.cluster import KMeans
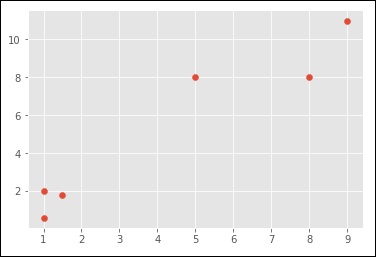
x = [1, 5, 1.5, 8, 1, 9]
y = [2, 8, 1.8, 8, 0.6, 11]
plt.scatter(x,y)
plt.show()
X = np.array([ [1, 2],
[5, 8],
[1.5, 1.8],
[8, 8],
[1, 0.6],
[9, 11]])
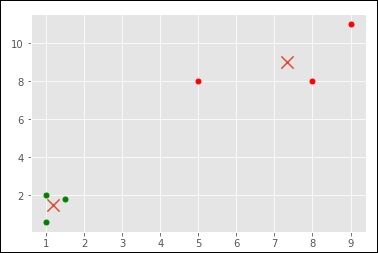
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
centroids = kmeans.cluster_centers_
labels = kmeans.labels_
print(centroids)
print(labels)
colors = ["g.","r.","c.","y."]
for i in range(len(X)):
print("coordinate:",X[i], "label:", labels[i])
plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 10)
plt.scatter(centroids[:, 0],centroids[:, 1], marker = "x", s=150, linewidths = 5, zorder = 10)
plt.show()
When you run the code given above, you can see the following output −
[ [ 1.16666667 1.46666667] [ 7.33333333 9. ] ]
[0 1 0 1 0 1]
('coordinate:', array([ 1., 2.]), 'label:', 0)
('coordinate:', array([ 5., 8.]), 'label:', 1)
('coordinate:', array([ 1.5, 1.8]), 'label:', 0)
('coordinate:', array([ 8., 8.]), 'label:', 1)
('coordinate:', array([ 1. , 0.6]), 'label:', 0)
('coordinate:', array([ 9., 11.]), 'label:', 1)
Here is another code for your understanding −
from sklearn.cluster import KMeans
df = pd.read_csv('iris_df.csv')
df.columns = ['X1', 'X2', 'X3', 'X4', 'Y']
df = df.drop(['X4', 'X3'], 1)
df.head()
from sklearn.cross_validation import train_test_split
kmeans = KMeans(n_clusters = 3)
X = df.values[:, 0:2]
kmeans.fit(X)
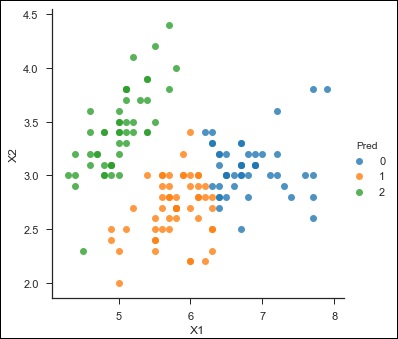
df['Pred'] = kmeans.predict(X)
df.head()
sns.set_context('notebook', font_scale = 1.1)
sns.set_style('ticks')
sns.lmplot('X1','X2', scatter = True, fit_reg = False, data = df, hue = 'Pred')
Here is the output of the above code −
<seaborn.axisgrid.FacetGrid at 0x107ad6a0>
Random Forest
Random Forest is a popular supervised ensemble learning algorithm. Ensemble means that it takes a bunch of weak learners and has them work together to form one strong predictor. In this case, the weak learners are all randomly implemented decision trees that are brought together to form the strong predictor a random forest.
Observe the following code −
from sklearn.ensemble import RandomForestClassifier
df = pd.read_csv('iris_df.csv')
df.columns = ['X1', 'X2', 'X3', 'X4', 'Y']
df.head()
from sklearn.cross_validation import train_test_split
forest = RandomForestClassifier()
X = df.values[:, 0:4]
Y = df.values[:, 4]
trainX, testX, trainY, testY = train_test_split( X, Y, test_size = 0.3)
forest.fit(trainX, trainY)
print('Accuracy: \n', forest.score(testX, testY))
pred = forest.predict(testX)
The output for the code given above is −
('Accuracy: \n', 1.0)
The goal of ensemble methods is to combine the predictions of several base estimators built with a given learning algorithm in order to improve generalizability / robustness over a single estimator.
The sklearn.ensemble module includes two averaging algorithms based on randomized decision trees - the RandomForest algorithm and the Extra-Trees method. Both algorithms are perturb-and-combine techniques [B1998] specifically designed for trees. This means a diverse set of classifiers is created by introducing randomness in the classifier construction. The prediction of the ensemble is given as the averaged prediction of the individual classifiers.
Forest classifiers have to be fitted with two arrays - a sparse or dense array X of size [n_samples, n_features] holding the training samples, and an array Y of size [n_samples] holding the target values (class labels) for the training samples, as shown in the code below −
>>> from sklearn.ensemble import RandomForestClassifier >>> X = [[0, 0], [1, 1]] >>> Y = [0, 1] >>> clf = RandomForestClassifier(n_estimators = 10) >>> clf = clf.fit(X, Y)
Like decision trees, forests of trees also extend to multi-output problems (if Y is an array of size [n_samples, n_outputs]).
In contrast to the original publication [B2001], the scikit-learn implementation combines classifiers by averaging their probabilistic prediction, instead of letting each classifier vote for a single class.
Random Forest is a trademark term for an ensemble of decision trees. In Random Forest, we have a collection of decision trees, known as Forest. To classify a new object based on attributes, each tree gives a classification and we say the tree votes for that class. The forest chooses the classification having the most votes (over all the trees in the forest).
Each tree is planted & grown as follows −
If the number of cases in the training set is N, then sample of N cases is taken at random but with replacement. This sample will be the training set for growing the tree.
If there are M input variables, a number m<<M is specified such that at each node, m variables are selected at random out of the M and the best split on these m is used to split the node. The value of m is held constant during the forest growing.
Each tree is grown to the largest extent possible. There is no pruning.
Dimensionality Reduction Algorithm
Dimensionality reduction is yet another common unsupervised learning task. Some problems may contain tens of thousands or even millions of input or explanatory variables, which can be costly to work with and do computations. Moreover, the program's ability to generalize may be diminished if some of the input variables capture noise or are not relevant to the underlying relationship.
Dimensionality reduction is the process of finding the input variables that are responsible for the greatest changes in the output or response variable. Dimensionality reduction is sometimes also used to visualize data. It is easy to visualize a regression problem such as predicting the price of a property from its size, where the size of the property can be plotted along graph's x axis, and the price of the property can be plotted along the y axis. Similarly, it is easy to visualize the property price regression problem when a second explanatory variable is added. The number of rooms in the property could be plotted on the z axis, for instance. A problem with thousands of input variables, however, becomes impossible to visualize.
Dimensionality reduction, reduces a very large set of input of explanatory variables to a smaller set of input variables that retain as much information as possible.
PCA is a dimensionality reduction algorithm that can do useful things for data analysis. Most importantly, it can dramatically reduce the number of computations involved in a model when dealing with hundreds or thousands of different input variables. As it is an unsupervised learning task, the user still has to analyze the results and make sure they are keeping 95% or so of the original datasets behavior.
Observe the following code for a better understanding −
from sklearn import decomposition
df = pd.read_csv('iris_df.csv')
df.columns = ['X1', 'X2', 'X3', 'X4', 'Y']
df.head()
from sklearn import decomposition
pca = decomposition.PCA()
fa = decomposition.FactorAnalysis()
X = df.values[:, 0:4]
Y = df.values[:, 4]
train, test = train_test_split(X,test_size = 0.3)
train_reduced = pca.fit_transform(train)
test_reduced = pca.transform(test)
pca.n_components_
You can see the following output for the code given above −
4L
In the last 5 years, there has been an exponential rise in data capturing at every possible level and point. Government Agencies/ Research Organizations/Corporates are not only coming out with new data sources, but also they are capturing very detailed data at several points and stages.
For example, e-commerce companies are capturing more details about customers like their demographics, browsing history, their likes or dislikes, purchase history, feedback and several other details to give them customized attention. The data that is now available may have thousands of features and reducing those features while retaining as much information as possible is a challenge. In such situations, dimensionality reduction helps a lot.
Boosting Algorithms
The term Boosting refers to a family of algorithms that converts weak learner to strong learners. Let us understand this definition by solving a problem of spam email identification as shown below −
What procedure should be followed to classify an email as SPAM or not? In initial approach, we would identify spam and not spam emails using following criteria if −
Email has only one image file (advertisement image), Its a SPAM
Email has only link(s), Its a SPAM
Email body consist of sentence like You won a prize money of $ xxxxxx, Its a SPAM
Email from our official domain Tutorialspoint.com , Not a SPAM
Email from known source, Not a SPAM
Above, we have defined several rules to classify an email into spam or not spam. These rules, however, individually are not strong enough to successfully classify an email into spam or not spam. Therefore, these rules are termed as weak learner.
To convert weak learner to strong learner, we combine the prediction of each weak learner using methods like −
- Using average/weighted average
- Considering prediction that has higher vote
For example, suppose we have defined 7 weak learners. Out of these 7, 5 are voted as SPAM and 2 are voted as Not a SPAM. In this case, by default, well consider an email as SPAM because we have higher (5) vote for SPAM.
How It Works
Boosting combines weak learner or base learner to form a strong rule. This section will explain you how boosting identifies weak rules.
To find weak rule, we apply base learning (ML) algorithms with a different distribution. Each time base learning algorithm is applied, it generates a new weak prediction rule. This uses iteration processes several times. After many iterations, the boosting algorithm combines these weak rules into a single strong prediction rule.
For choosing the right distribution for each round, follow the given steps −
Step 1 − The base learner takes all the distributions and assigns equal weight to each one.
Step 2 − If there is any prediction error caused by first base learning algorithm, then we pay higher weight to observations having prediction error. Then, we apply the next base learning algorithm.
We iterate Step 2 till the limit of base learning algorithm is attained or higher accuracy is achieved.
Finally, it combines the outputs from weak learner and makes a strong learner which eventually improves the prediction power of the model. Boosting lays more focus on examples which are wrongly classified or have higher errors by due to weak rules.
Types of Boosting Algorithms
There are several types of engine used for boosting algorithms - decision stump, margin-maximizing classification algorithm and so on. Different boosting algorithms are listed here −
- AdaBoost (Adaptive Boosting)
- Gradient Tree Boosting
- XGBoost
This section focuses on AdaBoost and Gradient Boosting followed by their respective Boosting Algorithms.
AdaBoost
Observe the following figure that explains Ada-boost algorithm.
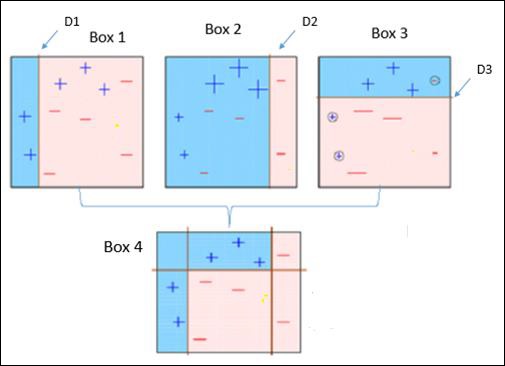
It is explained below −
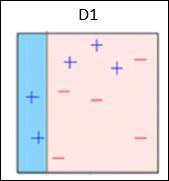
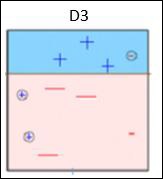
Box 1 − You can see that we have assigned equal weights to each data point and applied a decision stump to classify them as + (plus) or (minus). The decision stump (D1) has created a vertical line at left side to classify the data points. This vertical line has incorrectly predicted three + (plus) as (minus). So, well assign higher weights to these three + (plus) and apply another decision stump.
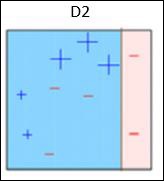
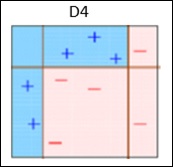
Box 2 − Here, it can see that the size of three (wrongly predicted) + (plus) data points is bigger as compared to rest of the data points. In this case, the second decision stump (D2) will try to predict them correctly. Now, a vertical line (D2) at right side of this box has classified three wrongly classified + (plus) correctly. But again, it has made mis-classification errors. This time with three -(minus) data points. Again, we will assign higher weights to the three (minus) data points and apply another decision stump.
Box 3 − Here, three (minus) data points are given higher weights. A decision stump (D3) is applied to predict these wrongly classified observations correctly. This time a horizontal line is generated to classify + (plus) and (minus) data points based on higher weight of wrongly classified observations.
Box 4 − Here, we have joined D1, D2 and D3 to form a strong prediction having complex rule as compared to individual weak learners. It can be seen that this algorithm has classified these observations quite well as compared to any of individual weak learner.
AdaBoost or Adaptive Boosting − It works on similar method as discussed above. It fits a sequence of weak learners on different weighted training data. It starts by predicting original data set and gives equal weight to each observation. If prediction is incorrect using the first learner, then it gives higher weight to observations which have been predicted incorrectly. Being an iterative process, it continues to add learner(s) until a limit is reached in the number of models or accuracy.
Mostly, we use decision stamps with AdaBoost. But, we can use any machine learning algorithms as base learner if it accepts weight on training data set. We can use AdaBoost algorithms for both classification and regression problems.
You can use the following Python code for this purpose −
#for classification from sklearn.ensemble import AdaBoostClassifier #for regression from sklearn.ensemble import AdaBoostRegressor from sklearn.tree import DecisionTreeClassifier dt = DecisionTreeClassifier() clf = AdaBoostClassifier(n_estimators=100, base_estimator=dt,learning_rate=1) #Here we have used decision tree as a base estimator; Any ML learner can be used as base #estimator if it accepts sample weight clf.fit(x_train,y_train)
Parameters for Tuning
The parameters can be tuned to optimize the performance of algorithms, The key parameters for tuning are −
n_estimators − These control the number of weak learners.
learning_rate − This controls the contribution of weak learners in the final combination. There is a trade-off between learning_rate and n_estimators.
base_estimators − These help to specify different ML algorithm.
The parameters of base learners can also be tuned to optimize its performance.
Gradient Boosting
In gradient boosting, many models are trained sequentially. Each new model gradually minimizes the loss function (y = ax + b + e, where e is the error term) of the whole system using Gradient Descent method. The learning method consecutively fits new models to give a more accurate estimate of the response variable.
The main idea behind this algorithm is to construct new base learners which can be optimally correlated with negative gradient of the loss function, relevant to the whole ensemble.
In Python Sklearn library, we use Gradient Tree Boosting or GBRT which is a generalization of boosting to arbitrary differentiable loss functions. It can be utilized for both regression and classification problems.
You can use the following code for this purpose −
#for classification from sklearn.ensemble import GradientBoostingClassifier #for regression from sklearn.ensemble import GradientBoostingRegressor clf = GradientBoostingClassifier(n_estimators = 100, learning_rate = 1.0, max_depth = 1) clf.fit(X_train, y_train)
Here are the terms used in the above code −
n_estimators − These control the number of weak learners.
learning_rate − This controls the contribution of weak learners in the final combination. There is a trade-off between learning_rate and n_estimators.
max_depth − This is the maximum depth of the individual regression estimators which limits the number of nodes in the tree. This parameter is tuned for best performance and the best value depends on the interaction of the input variables.
The loss function can be tuned for better performance.