DSP - Z-Transform Properties

---

---

In this chapter, we will understand the basic properties of Z-transforms.

Linearity

It states that when two or more individual discrete signals are multiplied by constants, their respective Z-transforms will also be multiplied by the same constants.

Mathematically,

$$a_1x_1(n)+a_2x_2(n) = a_1X_1(z)+a_2X_2(z)$$

Proof − We know that,

$$X(Z) = \sum_{n=-\infty}^\infty x(n)Z^{-n}$$

$= \sum_{n=-\infty}^\infty (a_1x_1(n)+a_2x_2(n))Z^{-n}$

$= a_1\sum_{n = -\infty}^\infty x_1(n)Z^{-n}+a_2\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= a_1X_1(z)+a_2X_2(z)$ (Hence Proved)

Here, the ROC is $ROC_1\bigcap ROC_2$.

Time Shifting

Time shifting property depicts how the change in the time domain in the discrete signal will affect the Z-domain, which can be written as;

$$x(n-n_0)\longleftrightarrow X(Z)Z^{-n}$$

Or $x(n-1)\longleftrightarrow Z^{-1}X(Z)$

Proof −

Let $y(P) = X(P-K)$

$Y(z) = \sum_{p = -\infty}^\infty y(p)Z^{-p}$

$= \sum_{p = -\infty}^\infty (x(p-k))Z^{-p}$

Let s = p-k

$= \sum_{s = -\infty}^\infty x(s)Z^{-(s+k)}$

$= \sum_{s = -\infty}^\infty x(s)Z^{-s}Z^{-k}$

$= Z^{-k}[\sum_{s=-\infty}^\infty x(m)Z^{-s}]$

$= Z^{-k}X(Z)$ (Hence Proved)

Here, ROC can be written as Z = 0 (p>0) or Z = ∞(p<0)

Example

U(n) and U(n-1) can be plotted as follows

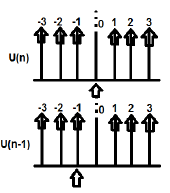
Z-transformation of U(n) cab be written as;

$\sum_{n = -\infty}^\infty [U(n)]Z^{-n} = 1$

Z-transformation of U(n-1) can be written as;

$\sum_{n = -\infty}^\infty [U(n-1)]Z^{-n} = Z^{-1}$

So here $x(n-n_0) = Z^{-n_0}X(Z)$ (Hence Proved)

Time Scaling

Time Scaling property tells us, what will be the Z-domain of the signal when the time is scaled in its discrete form, which can be written as;

$$a^nx(n) \longleftrightarrow X(a^{-1}Z)$$

Proof −

Let $y(p) = a^{p}x(p)$

$Y(P) = \sum_{p=-\infty}^\infty y(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty a^px(p)Z^{-p}$

$= \sum_{p=-\infty}^\infty x(p)[a^{-1}Z]^{-p}$

$= X(a^{-1}Z)$(Hence proved)

ROC: = Mod(ar1) < Mod(Z) < Mod(ar2) where Mod = Modulus

Example

Let us determine the Z-transformation of $x(n) = a^n \cos \omega n$ using Time scaling property.

Solution −

We already know that the Z-transformation of the signal $\cos (\omega n)$ is given by −

$$\sum_{n=-\infty}^\infty(\cos \omega n)Z^{-n} = (Z^2-Z \cos \omega)/(Z^2-2Z\cos \omega +1)$$

Now, applying Time scaling property, the Z-transformation of $a^n \cos \omega n$ can be written as;

$\sum_{n=-\infty}^\infty(a^n\cos \omega n)Z^{-n} = X(a^{-1}Z)$

$= [(a^{-1}Z)^2-(a^{-1}Z \cos \omega n)]/((a^{-1}Z)^2-2(a^{-1}Z \cos \omega n)+1)$

$= Z(Z-a \cos \omega)/(Z^2-2az \cos \omega+a^2)$

Successive Differentiation

Successive Differentiation property shows that Z-transform will take place when we differentiate the discrete signal in time domain, with respect to time. This is shown as below.

$$\frac{dx(n)}{dn} = (1-Z^{-1})X(Z)$$

Proof −

Consider the LHS of the equation − $\frac{dx(n)}{dn}$

$$= \frac{[x(n)-x(n-1)]}{[n-(n-1)]}$$

$= x(n)-X(n-1)$

$= x(Z)-Z^{-1}x(Z)$

$= (1-Z^{-1})x(Z)$ (Hence Proved)

ROC: R1< Mod (Z) <R2

Example

Let us find the Z-transform of a signal given by $x(n) = n^2u(n)$

By property we can write

$Zz[nU(n)] = -Z\frac{dZ[U(n)]}{dz}$

$= -Z\frac{d[\frac{Z}{Z-1}]}{dZ}$

$= Z/((Z-1)^2$

$= y(let)$

Now, Z[n.y] can be found out by again applying the property,

$Z(n,y) = -Z\frac{dy}{dz}$

$= -Z\frac{d[Z/(Z-1)^3]}{dz}$

$= Z(Z+1)/(Z-1)^2$

Convolution

This depicts the change in Z-domain of the system when a convolution takes place in the discrete signal form, which can be written as −

$x_1(n)*x_2(n) \longleftrightarrow X_1(Z).X_2(Z)$

Proof −

$X(Z) = \sum_{n = -\infty}^\infty x(n)Z^{-n}$

$= \sum_{n=-\infty}^\infty[\sum_{k = -\infty}^\infty x_1(k)x_2(n-k)]Z^{-n}$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_n^\infty x_2(n-k)Z^{-n}]$

$= \sum_{k = -\infty}^\infty x_1(k)[\sum_{n = -\infty}^\infty x_2(n-k)Z^{-(n-k)}Z^{-k}]$

Let n-k = l, then the above equation cab be written as −

$X(Z) = \sum_{k = -\infty}^\infty x_1(k)[Z^{-k}\sum_{l=-\infty}^\infty x_2(l)Z^{-l}]$

$= \sum_{k = -\infty}^\infty x_1(k)X_2(Z)Z^{-k}$

$= X_2(Z)\sum_{k = -\infty}^\infty x_1(Z)Z^{-k}$

$= X_1(Z).X_2(Z)$ (Hence Proved)

ROC:$ROC\bigcap ROC2$

Example

Let us find the convolution given by two signals

$x_1(n) = \lbrace 3,-2,2\rbrace$ ...(eq. 1)

$x_2(n) = \lbrace 2,0\leq 4\quad and\quad 0\quad elsewhere\rbrace$ ...(eq. 2)

Z-transformation of the first equation can be written as;

$\sum_{n = -\infty}^\infty x_1(n)Z^{-n}$

$= 3-2Z^{-1}+2Z^{-2}$

Z-transformation of the second signal can be written as;

$\sum_{n = -\infty}^\infty x_2(n)Z^{-n}$

$= 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

So, the convolution of the above two signals is given by −

$X(Z) = [x_1(Z)^*x_2(Z)]$

$= [3-2Z^{-1}+2Z^{-2}]\times [2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}]$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+...\quad...\quad...$

Taking the inverse Z-transformation we get,

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$

Initial Value Theorem

If x(n) is a causal sequence, which has its Z-transformation as X(z), then the initial value theorem can be written as;

$X(n)(at\quad n = 0) = \lim_{z \to \infty} X(z)$

Proof − We know that,

$X(Z) = \sum_{n = 0} ^\infty x(n)Z^{-n}$

Expanding the above series, we get;

$= X(0)Z^0+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

$= X(0)\times 1+X(1)Z^{-1}+X(2)Z^{-2}+...\quad...$

In the above case if Z → ∞ then $Z^{-n}\rightarrow 0$ (Because n>0)

Therefore, we can say;

$\lim_{z \to \infty}X(z) = X(0)$ (Hence Proved)

Final Value Theorem

Final Value Theorem states that if the Z-transform of a signal is represented as X(Z) and the poles are all inside the circle, then its final value is denoted as x(n) or X(∞) and can be written as −

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$

Conditions −

• It is applicable only for causal systems.
• $X(Z)(1-Z^{-1})$ should have poles inside the unit circle in Z-plane.

Proof − We know that

$Z^+[x(n+1)-x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z^+[x(n+1)]-Z^+[x(n)] = \lim_{k \to \infty}\sum_{n=0}^kZ^{-n}[x(n+1)-x(n)]$

$\Rightarrow Z[X(Z)^+-x(0)]-X(Z)^+ = \lim_{k \to \infty}\sum_{n = 0}^kZ^{-n}[x(n+1)-x(n)]$

Here, we can apply advanced property of one-sided Z-Transformation. So, the above equation can be re-written as;

$Z^+[x(n+1)] = Z[X(2)^+-x(0)Z^0] = Z[X(Z)^+-x(0)]$

Now putting z = 1 in the above equation, we can expand the above equation −

$\lim_{k \to \infty}{[x(1)-x(0)+x(6)-x(1)+x(3)-x(2)+...\quad...\quad...+x(x+1)-x(k)]}$

This can be formulated as;

$X(\infty) = \lim_{n \to \infty}X(n) = \lim_{z \to 1}[X(Z)(1-Z^{-1})]$(Hence Proved)

Example

Let us find the Initial and Final value of x(n) whose signal is given by

$X(Z) = 2+3Z^{-1}+4Z^{-2}$

Solution − Let us first, find the initial value of the signal by applying the theorem

$x(0) = \lim_{z \to \infty}X(Z)$

$= \lim_{z \to \infty}[2+3Z^{-1}+4Z^{-2}]$

$= 2+(\frac{3}{\infty})+(\frac{4}{\infty}) = 2$

Now let us find the Final value of signal applying the theorem

$x(\infty) = \lim_{z \to \infty}[(1-Z^{-1})X(Z)]$

$= \lim_{z \to \infty}[(1-Z^{-1})(2+3Z^{-1}+4Z^{-2})]$

$= \lim_{z \to \infty}[2+Z^{-1}+Z^{-2}-4Z^{-3}]$

$= 2+1+1-4 = 0$

Some other properties of Z-transform are listed below −

Differentiation in Frequency

It gives the change in Z-domain of the signal, when its discrete signal is differentiated with respect to time.

$nx(n)\longleftrightarrow -Z\frac{dX(z)}{dz}$

Its ROC can be written as;

$r_2< Mod(Z)< r_1$

Example

Let us find the value of x(n) through Differentiation in frequency, whose discrete signal in Z-domain is given by $x(n)\longleftrightarrow X(Z) = log(1+aZ^{-1})$

By property, we can write that

$nx(n)\longleftrightarrow -Z\frac{dx(Z)}{dz}$

$= -Z[\frac{-aZ^{-2}}{1+aZ^{-1}}]$

$= (aZ^{-1})/(1+aZ^{-1})$

$= 1-1/(1+aZ^{-1})$

$nx(n) = \delta(n)-(-a)^nu(n)$

$\Rightarrow x(n) = 1/n[\delta(n)-(-a)^nu(n)]$

Multiplication in Time

It gives the change in Z-domain of the signal when multiplication takes place at discrete signal level.

$x_1(n).x_2(n)\longleftrightarrow(\frac{1}{2\Pi j})[X1(Z)*X2(Z)]$

Conjugation in Time

This depicts the representation of conjugated discrete signal in Z-domain.

$X^*(n)\longleftrightarrow X^*(Z^*)$