- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
DSP - Operations on Signals Shifting
Shifting means movement of the signal, either in time domain (around Y-axis) or in amplitude domain (around X-axis). Accordingly, we can classify the shifting into two categories named as Time shifting and Amplitude shifting, these are subsequently discussed below.
Time Shifting
Time shifting means, shifting of signals in the time domain. Mathematically, it can be written as
$$x(t) \rightarrow y(t+k)$$This K value may be positive or it may be negative. According to the sign of k value, we have two types of shifting named as Right shifting and Left shifting.
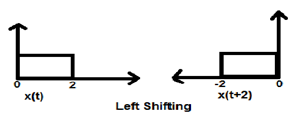
Case 1 (K > 0)
When K is greater than zero, the shifting of the signal takes place towards "left" in the time domain. Therefore, this type of shifting is known as Left Shifting of the signal.
Example
Case 2 (K < 0)
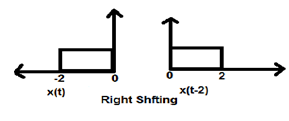
When K is less than zero the shifting of signal takes place towards right in the time domain. Therefore, this type of shifting is known as Right shifting.
Example
The figure given below shows right shifting of a signal by 2.
Amplitude Shifting
Amplitude shifting means shifting of signal in the amplitude domain (around X-axis). Mathematically, it can be represented as −
$$x(t) \rightarrow x(t)+K$$This K value may be positive or negative. Accordingly, we have two types of amplitude shifting which are subsequently discussed below.
Case 1 (K > 0)
When K is greater than zero, the shifting of signal takes place towards up in the x-axis. Therefore, this type of shifting is known as upward shifting.
Example
Let us consider a signal x(t) which is given as;
$$x = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$Let we have taken K=+1 so new signal can be written as −
$y(t) \rightarrow x(t)+1$ So, y(t) can finally be written as;
$$x(t) = \begin{cases}1, & t < 0\\2, & 0\leq t\leq 2\\ 1, & t>0\end{cases}$$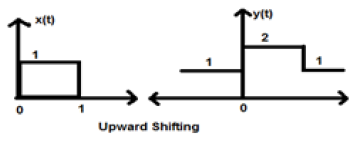
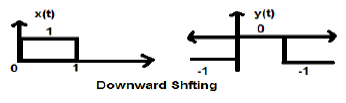
Case 2 (K < 0)
When K is less than zero shifting of signal takes place towards downward in the X- axis. Therefore, it is called downward shifting of the signal.
Example
Let us consider a signal x(t) which is given as;
$$x(t) = \begin{cases}0, & t < 0\\1, & 0\leq t\leq 2\\ 0, & t>0\end{cases}$$Let we have taken K = -1 so new signal can be written as;
$y(t)\rightarrow x(t)-1$ So, y(t) can finally be written as;
$$y(t) = \begin{cases}-1, & t < 0\\0, & 0\leq t\leq 2\\ -1, & t>0\end{cases}$$