
- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
Digital Signal Processing - Signals-Definition
Definition
Anything that carries information can be called as signal. It can also be defined as a physical quantity that varies with time, temperature, pressure or with any independent variables such as speech signal or video signal.
The process of operation in which the characteristics of a signal (Amplitude, shape, phase, frequency, etc.) undergoes a change is known as signal processing.
Note − Any unwanted signal interfering with the main signal is termed as noise. So, noise is also a signal but unwanted.
According to their representation and processing, signals can be classified into various categories details of which are discussed below.
Continuous Time Signals
Continuous-time signals are defined along a continuum of time and are thus, represented by a continuous independent variable. Continuous-time signals are often referred to as analog signals.
This type of signal shows continuity both in amplitude and time. These will have values at each instant of time. Sine and cosine functions are the best example of Continuous time signal.
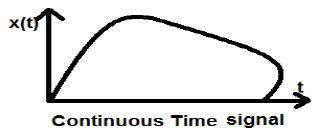
The signal shown above is an example of continuous time signal because we can get value of signal at each instant of time.
Discrete Time signals
The signals, which are defined at discrete times are known as discrete signals. Therefore, every independent variable has distinct value. Thus, they are represented as sequence of numbers.
Although speech and video signals have the privilege to be represented in both continuous and discrete time format; under certain circumstances, they are identical. Amplitudes also show discrete characteristics. Perfect example of this is a digital signal; whose amplitude and time both are discrete.
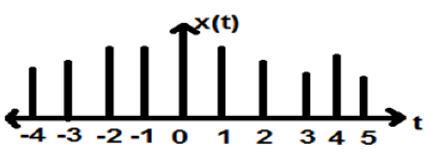
The figure above depicts a discrete signals discrete amplitude characteristic over a period of time. Mathematically, these types of signals can be formularized as;
$$x = \left \{ x\left [ n \right ] \right \},\quad -\infty < n< \infty$$Where, n is an integer.
It is a sequence of numbers x, where nth number in the sequence is represented as x[n].