
- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
DSP - Operations on Signals Convolution
The convolution of two signals in the time domain is equivalent to the multiplication of their representation in frequency domain. Mathematically, we can write the convolution of two signals as
$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$Steps for convolution
- Take signal x1(t) and put t = p there so that it will be x1(p).
- Take the signal x2(t) and do the step 1 and make it x2(p).
- Make the folding of the signal i.e. x2(-p).
- Do the time shifting of the above signal x2[-(p-t)]
- Then do the multiplication of both the signals. i.e. $x_{1}(p).x_{2}[(pt)]$
Example
Let us do the convolution of a step signal u(t) with its own kind.
$y(t) = u(t)*u(t)$
$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$
Now this t can be greater than or less than zero, which are shown in below figures
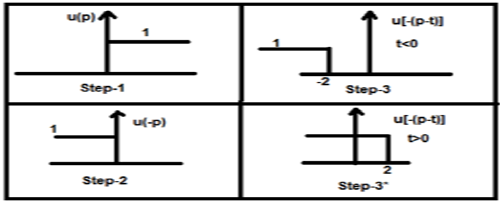
So, with the above case, the result arises with following possibilities
$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$
$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$
Properties of Convolution
Commutative
It states that order of convolution does not matter, which can be shown mathematically as
$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$Associative
It states that order of convolution involving three signals, can be anything. Mathematically, it can be shown as;
$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$Distributive
Two signals can be added first, and then their convolution can be made to the third signal. This is equivalent to convolution of two signals individually with the third signal and added finally. Mathematically, this can be written as;
$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$Area
If a signal is the result of convolution of two signals then the area of the signal is the multiplication of those individual signals. Mathematically this can be written
If $y(t) = x_{1}*x_{2}(t)$
Then, Area of y(t) = Area of x1(t) X Area of x2(t)
Scaling
If two signals are scaled to some unknown constant a and convolution is done then resultant signal will also be convoluted to same constant a and will be divided by that quantity as shown below.
If, $x_{1}(t)*x_{2}(t) = y(t)$
Then, $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$
Delay
Suppose a signal y(t) is a result from the convolution of two signals x1(t) and x2(t). If the two signals are delayed by time t1 and t2 respectively, then the resultant signal y(t) will be delayed by (t1+t2). Mathematically, it can be written as −
If, $x_{1}(t)*x_{2}(t) = y(t)$
Then, $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$
Solved Examples
Example 1 − Find the convolution of the signals u(t-1) and u(t-2).
Solution − Given signals are u(t-1) and u(t-2). Their convolution can be done as shown below −
$y(t) = u(t-1)*u(t-2)$
$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$
$= r(t-1)+r(t-2)$
$= r(t-3)$
Example 2 − Find the convolution of two signals given by
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$
Solution −
x2(n) can be decoded as $x_{2}(n) = \lbrace 2,2,2,2,2\rbrace Originalfirst$
x1(n) is previously given $= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$
Similarly, $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$
Resultant signal,
$X(Z) = X_{1}(Z)X_{2}(z)$
$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$
$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$
Taking inverse Z-transformation of the above, we will get the resultant signal as
$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ Origin at the first
Example 3 − Determine the convolution of following 2 signals −
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution −
Taking the Z-transformation of the signals, we get,
$x(z) = 2+2Z^{-1}+2Z^{-3}$
And $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$
Now convolution of two signal means multiplication of their Z-transformations
That is $Y(Z) = X(Z) \times h(Z)$
$= \lbrace 2+2Z^{-1}+2Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$
$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+3Z^{-5}+Z^{-6}\rbrace$
Taking the inverse Z-transformation, the resultant signal can be written as;
$y(n) = \lbrace 2,5,8,6,6,1 \rbrace Originalfirst$