- Digital Signal Processing Tutorial
- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations on Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
DSP - Classification of DT Signals
Just like Continuous time signals, Discrete time signals can be classified according to the conditions or operations on the signals.
Even and Odd Signals
Even Signal
A signal is said to be even or symmetric if it satisfies the following condition;
$$x(-n) = x(n)$$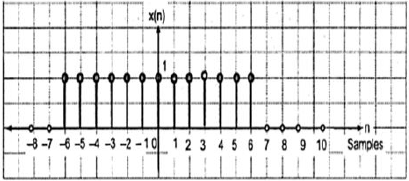
Here, we can see that x(-1) = x(1), x(-2) = x(2) and x(-n) = x(n). Thus, it is an even signal.
Odd Signal
A signal is said to be odd if it satisfies the following condition;
$$x(-n) = -x(n)$$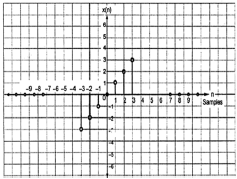
From the figure, we can see that x(1) = -x(-1), x(2) = -x(2) and x(n) = -x(-n). Hence, it is an odd as well as anti-symmetric signal.
Periodic and Non-Periodic Signals
A discrete time signal is periodic if and only if, it satisfies the following condition −
$$x(n+N) = x(n)$$Here, x(n) signal repeats itself after N period. This can be best understood by considering a cosine signal −
$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$For the signal to become periodic, following condition should be satisfied;
$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$i.e. $2\pi f_{0}N$ is an integral multiple of $2\pi$
$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$Frequencies of discrete sinusoidal signals are separated by integral multiple of $2\pi$.
Energy and Power Signals
Energy Signal
Energy of a discrete time signal is denoted as E. Mathematically, it can be written as;
$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$If each individual values of $x(n)$ are squared and added, we get the energy signal. Here $x(n)$ is the energy signal and its energy is finite over time i.e $0< E< \infty$
Power Signal
Average power of a discrete signal is represented as P. Mathematically, this can be written as;
$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$Here, power is finite i.e. 0<P<∞. However, there are some signals, which belong to neither energy nor power type signal.