- Digital Signal Processing Tutorial
- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations on Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
DSP - Operations on Signals Reversal
Whenever the time in a signal gets multiplied by -1, the signal gets reversed. It produces its mirror image about Y or X-axis. This is known as Reversal of the signal.
Reversal can be classified into two types based on the condition whether the time or the amplitude of the signal is multiplied by -1.
Time Reversal
Whenever signal’s time is multiplied by -1, it is known as time reversal of the signal. In this case, the signal produces its mirror image about Y-axis. Mathematically, this can be written as;
$$x(t) \rightarrow y(t) \rightarrow x(-t)$$This can be best understood by the following example.
In the above example, we can clearly see that the signal has been reversed about its Y-axis. So, it is one kind of time scaling also, but here the scaling quantity is (-1) always.
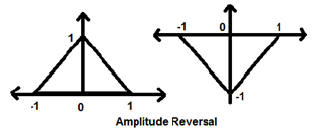
Amplitude Reversal
Whenever the amplitude of a signal is multiplied by -1, then it is known as amplitude reversal. In this case, the signal produces its mirror image about X-axis. Mathematically, this can be written as;
$$x(t)\rightarrow y(t)\rightarrow -x(t)$$Consider the following example. Amplitude reversal can be seen clearly.
