
- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
DSP - DFT Sectional Convolution
Suppose, the input sequence x(n) of long duration is to be processed with a system having finite duration impulse response by convolving the two sequences. Since, the linear filtering performed via DFT involves operation on a fixed size data block, the input sequence is divided into different fixed size data block before processing.
The successive blocks are then processed one at a time and the results are combined to produce the net result.
As the convolution is performed by dividing the long input sequence into different fixed size sections, it is called sectioned convolution. A long input sequence is segmented to fixed size blocks, prior to FIR filter processing.
Two methods are used to evaluate the discrete convolution −
Overlap-save method
Overlap-add method
Overlap Save Method
Overlapsave is the traditional name for an efficient way to evaluate the discrete convolution between a very long signal x(n) and a finite impulse response (FIR) filter h(n). Given below are the steps of Overlap save method −
Let the length of input data block = N = L+M-1. Therefore, DFT and IDFT length = N. Each data block carries M-1 data points of previous block followed by L new data points to form a data sequence of length N = L+M-1.
First, N-point DFT is computed for each data block.
By appending (L-1) zeros, the impulse response of FIR filter is increased in length and N point DFT is calculated and stored.
Multiplication of two N-point DFTs H(k) and Xm(k) : Y′m(k) = H(k).Xm(k), where K=0,1,2,N-1
Then, IDFT[Y′m((k)] = y′((n) = [y′m(0), y′m(1), y′m(2),.......y′m(M-1), y′m(M),.......y′m(N-1)]
(here, N-1 = L+M-2)
First M-1 points are corrupted due to aliasing and hence, they are discarded because the data record is of length N.
The last L points are exactly same as a result of convolution, so
y′m (n) = ym(n) where n = M, M+1,.N-1
To avoid aliasing, the last M-1 elements of each data record are saved and these points carry forward to the subsequent record and become 1st M-1 elements.
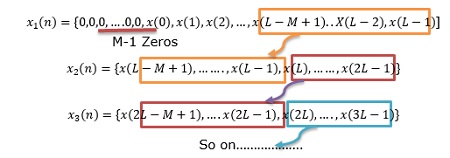
Result of IDFT, where first M-1 Points are avoided, to nullify aliasing and remaining L points constitute desired result as that of a linear convolution.
Overlap Add Method
Given below are the steps to find out the discrete convolution using Overlap method −
Let the input data block size be L. Therefore, the size of DFT and IDFT: N = L+M-1
Each data block is appended with M-1 zeros to the last.
Compute N-point DFT.

Two N-point DFTs are multiplied: Ym(k) = H(k).Xm(k), where k = 0,,1,2,.,N-1
IDFT [Ym(k)] produces blocks of length N which are not affected by aliasing as the size of DFT is N = L+M-1 and increased lengths of the sequences to N-points by appending M-1 zeros to each block.
Last M-1 points of each block must be overlapped and added to first M-1 points of the succeeding block.
(reason: Each data block terminates with M-1 zeros)
Hence, this method is known Overlap-add method. Thus, we get −
y(n) = {y1(0), y1(1), y1(2), ... .., y1(L-1), y1(L)+y2(0), y1(L+1)+y2(1), ... ... .., y1(N-1)+y2(M-1),y2(M), ... ... ... ... ... }