
- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
DSP - Operations on Signals Differentiation
Two very important operations performed on the signals are Differentiation and Integration.
Differentiation
Differentiation of any signal x(t) means slope representation of that signal with respect to time. Mathematically, it is represented as;
$$x(t)\rightarrow \frac{dx(t)}{dt}$$In the case of OPAMP differentiation, this methodology is very helpful. We can easily differentiate a signal graphically rather than using the formula. However, the condition is that the signal must be either rectangular or triangular type, which happens in most cases.
| Original Signal | Differentiated Signal |
|---|---|
| Ramp | Step |
| Step | Impulse |
| Impulse | 1 |
The above table illustrates the condition of the signal after being differentiated. For example, a ramp signal converts into a step signal after differentiation. Similarly, a unit step signal becomes an impulse signal.
Example
Let the signal given to us be $x(t) = 4[r(t)-r(t-2)]$. When this signal is plotted, it will look like the one on the left side of the figure given below. Now, our aim is to differentiate the given signal.
To start with, we will start differentiating the given equation. We know that the ramp signal after differentiation gives unit step signal.
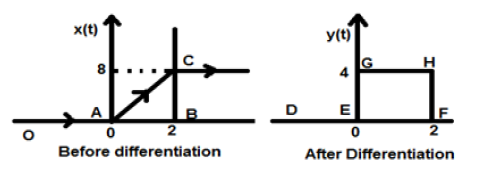
So our resulting signal y(t) can be written as;
$y(t) = \frac{dx(t)}{dt}$
$= \frac{d4[r(t)-r(t-2)]}{dt}$
$= 4[u(t)-u(t-2)]$
Now this signal is plotted finally, which is shown in the right hand side of the above figure.