- DSP - Home
- DSP - Signals-Definition
- DSP - Basic CT Signals
- DSP - Basic DT Signals
- DSP - Classification of CT Signals
- DSP - Classification of DT Signals
- DSP - Miscellaneous Signals
- Operations Signals - Shifting
- Operations Signals - Scaling
- Operations Signals - Reversal
- Operations Signals - Differentiation
- Operations Signals - Integration
- Operations Signals - Convolution
- Basic System Properties
- DSP - Static Systems
- DSP - Dynamic Systems
- DSP - Causal Systems
- DSP - Non-Causal Systems
- DSP - Anti-Causal Systems
- DSP - Linear Systems
- DSP - Non-Linear Systems
- DSP - Time-Invariant Systems
- DSP - Time-Variant Systems
- DSP - Stable Systems
- DSP - Unstable Systems
- DSP - Solved Examples
- Z-Transform
- Z-Transform - Introduction
- Z-Transform - Properties
- Z-Transform - Existence
- Z-Transform - Inverse
- Z-Transform - Solved Examples
- Discrete Fourier Transform
- DFT - Introduction
- DFT - Time Frequency Transform
- DTF - Circular Convolution
- DFT - Linear Filtering
- DFT - Sectional Convolution
- DFT - Discrete Cosine Transform
- DFT - Solved Examples
- Fast Fourier Transform
- DSP - Fast Fourier Transform
- DSP - In-Place Computation
- DSP - Computer Aided Design
- Digital Signal Processing Resources
- DSP - Quick Guide
- DSP - Useful Resources
- DSP - Discussion
DSP - Fast Fourier Transform
In earlier DFT methods, we have seen that the computational part is too long. We want to reduce that. This can be done through FFT or fast Fourier transform. So, we can say FFT is nothing but computation of discrete Fourier transform in an algorithmic format, where the computational part will be reduced.
The main advantage of having FFT is that through it, we can design the FIR filters. Mathematically, the FFT can be written as follows;
$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$Let us take an example to understand it better. We have considered eight points named from $x_0\quad to\quad x_7$. We will choose the even terms in one group and the odd terms in the other. Diagrammatic view of the above said has been shown below −
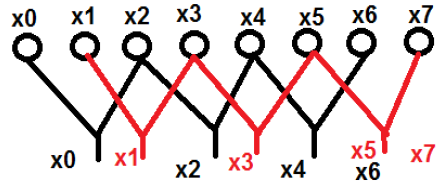
Here, points x0, x2, x4 and x6 have been grouped into one category and similarly, points x1, x3, x5 and x7 has been put into another category. Now, we can further make them in a group of two and can proceed with the computation. Now, let us see how these breaking into further two is helping in computation.
$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$
$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$
$= G[k]+H[k]\times W_N^k$
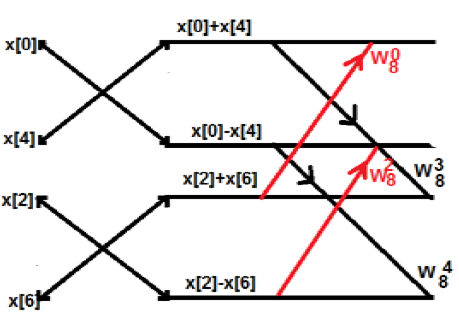
Initially, we took an eight-point sequence, but later we broke that one into two parts G[k] and H[k]. G[k] stands for the even part whereas H[k] stands for the odd part. If we want to realize it through a diagram, then it can be shown as below −
![Eight Point H[k]G[k]1](/digital_signal_processing/images/eight_point_h_g1.jpg)
![Eight Point H[k]G[k]2](/digital_signal_processing/images/eight_point_h_g2.jpg)
From the above figure, we can see that
$W_8^4 = -1$
$W_8^5 = -W_8^1$
$W_8^6 = -W_8^2$
$W_8^7 = -W_8^3$
Similarly, the final values can be written as follows −
$G[0]-H[0] = x[4]$
$G[1]-W_8^1H[1] = x[5]$
$G[2]-W_8^2H[2] = x[6]$
$G[1]-W_8^3H[3] = x[7]$
The above one is a periodic series. The disadvantage of this system is that K cannot be broken beyond 4 point. Now Let us break down the above into further. We will get the structures something like this
Example
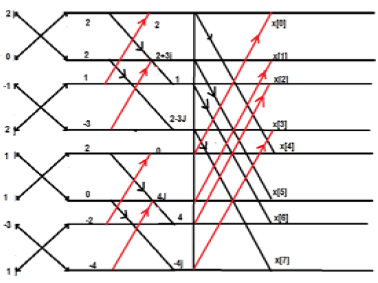
Consider the sequence x[n]={ 2,1,-1,-3,0,1,2,1}. Calculate the FFT.
Solution − The given sequence is x[n]={ 2,1,-1,-3,0,1,2,1}
Arrange the terms as shown below;