Arden's Theorem

---

---

In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.

Statement −

Let P and Q be two regular expressions.

If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*

Proof −

R = Q + (Q + RP)P [After putting the value R = Q + RP]

= Q + QP + RPP

When we put the value of R recursively again and again, we get the following equation −

R = Q + QP + QP² + QP³…..

R = Q (ε + P + P² + P³ + …. )

R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]

Hence, proved.

Assumptions for Applying Arden’s Theorem

• The transition diagram must not have NULL transitions
• It must have only one initial state

Method

Step 1 − Create equations as the following form for all the states of the DFA having n states with initial state q₁.

q₁ = q₁R₁₁ + q₂R₂₁ + … + q_nR_n1 + ε

q₂ = q₁R₁₂ + q₂R₂₂ + … + q_nR_n2

…………………………

…………………………

…………………………

…………………………

q_n = q₁R_1n + q₂R_2n + … + q_nR_nn

R_ij represents the set of labels of edges from q_i to q_j, if no such edge exists, then R_ij = ∅

Step 2 − Solve these equations to get the equation for the final state in terms of R_ij

Problem

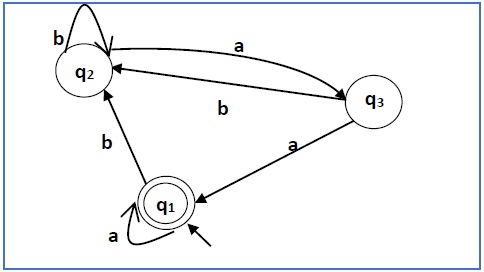
Construct a regular expression corresponding to the automata given below −

Solution −

Here the initial state and final state is q₁.

The equations for the three states q1, q2, and q3 are as follows −

q₁ = q₁a + q₃a + ε (ε move is because q1 is the initial state0

q₂ = q₁b + q₂b + q₃b

q₃ = q₂a

Now, we will solve these three equations −

q₂ = q₁b + q₂b + q₃b

= q₁b + q₂b + (q₂a)b (Substituting value of q₃)

= q₁b + q₂(b + ab)

= q₁b (b + ab)* (Applying Arden’s Theorem)

q₁ = q₁a + q₃a + ε

= q₁a + q₂aa + ε (Substituting value of q₃)

= q₁a + q₁b(b + ab*)aa + ε (Substituting value of q₂)

= q₁(a + b(b + ab)*aa) + ε

= ε (a+ b(b + ab)*aa)*

= (a + b(b + ab)*aa)*

Hence, the regular expression is (a + b(b + ab)*aa)*.

Problem

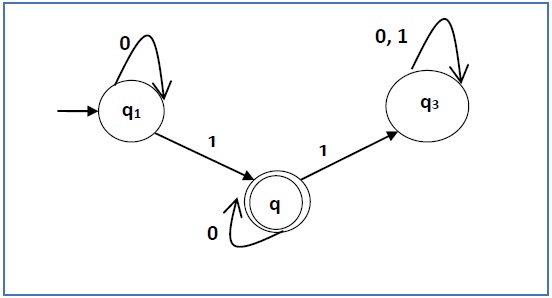
Construct a regular expression corresponding to the automata given below −

Solution −

Here the initial state is q₁ and the final state is q₂

Now we write down the equations −

q₁ = q₁0 + ε

q₂ = q₁1 + q₂0

q₃ = q₂1 + q₃0 + q₃1

Now, we will solve these three equations −

q₁ = ε0* [As, εR = R]

So, q₁ = 0*

q₂ = 0*1 + q₂0

So, q₂ = 0*1(0)* [By Arden’s theorem]

Hence, the regular expression is 0*10*.