
- Automata Theory Tutorial
- Automata Theory - Home
- Automata Theory Introduction
- Deterministic Finite Automaton
- Non-deterministic Finite Automaton
- NDFA to DFA Conversion
- DFA Minimization
- Moore & Mealy Machines
- Classification of Grammars
- Introduction to Grammars
- Language Generated by Grammars
- Chomsky Grammar Classification
- Regular Grammar
- Regular Expressions
- Regular Sets
- Arden's Theorem
- Constructing FA from RE
- Pumping Lemma for Regular Grammar
- DFA Complement
- Context-Free Grammars
- Context-Free Grammar Introduction
- Ambiguity in Grammar
- CFL Closure Properties
- CFG Simplification
- Chomsky Normal Form
- Greibach Normal Form
- Pumping Lemma for CFG
- Pushdown Automata
- Pushdown Automata Introduction
- Pushdown Automata Acceptance
- PDA & Context Free Grammar
- PDA & Parsing
- Turing Machine
- Turing Machine Introduction
- Accepted & Decided Language
- Multi-tape Turing Machine
- Multi-Track Turing Machine
- Non-Deterministic Turing Machine
- Semi-Infinite Tape Turing Machine
- Linear Bounded Automata
- Decidability
- Language Decidability
- Undecidable Language
- Turing Machine Halting Problem
- Rice Theorem
- Post Correspondence Problem
- Automata Theory Useful Resources
- Automata Theory - Quick Guide
- Automata Theory - Useful Resources
- Automata Theory - Discussion
Multi-tape Turing Machine
Multi-tape Turing Machines have multiple tapes where each tape is accessed with a separate head. Each head can move independently of the other heads. Initially the input is on tape 1 and others are blank. At first, the first tape is occupied by the input and the other tapes are kept blank. Next, the machine reads consecutive symbols under its heads and the TM prints a symbol on each tape and moves its heads.
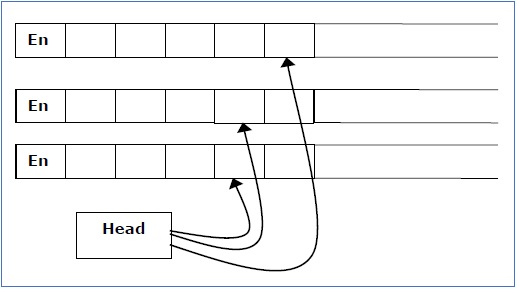
A Multi-tape Turing machine can be formally described as a 6-tuple (Q, X, B, δ, q0, F) where −
Q is a finite set of states
X is the tape alphabet
B is the blank symbol
δ is a relation on states and symbols where
δ: Q × Xk → Q × (X × {Left_shift, Right_shift, No_shift })k
where there is k number of tapes
q0 is the initial state
F is the set of final states
Note − Every Multi-tape Turing machine has an equivalent single-tape Turing machine.
To Continue Learning Please Login