Deterministic Finite Automaton

---

Finite Automaton can be classified into two types −

• Deterministic Finite Automaton (DFA)
• Non-deterministic Finite Automaton (NDFA / NFA)

Deterministic Finite Automaton (DFA)

In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.

Formal Definition of a DFA

A DFA can be represented by a 5-tuple (Q, ∑, δ, q₀, F) where −

• Q is a finite set of states.

• ∑ is a finite set of symbols called the alphabet.

• δ is the transition function where δ: Q × ∑ → Q

• q₀ is the initial state from where any input is processed (q₀ ∈ Q).

• F is a set of final state/states of Q (F ⊆ Q).

Graphical Representation of a DFA

A DFA is represented by digraphs called state diagram.

• The vertices represent the states.
• The arcs labeled with an input alphabet show the transitions.
• The initial state is denoted by an empty single incoming arc.
• The final state is indicated by double circles.

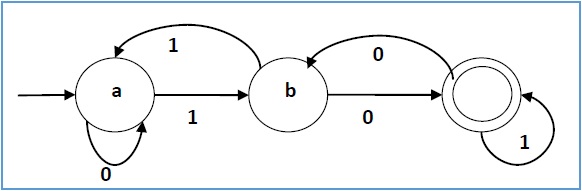
Example

Let a deterministic finite automaton be →

• Q = {a, b, c},
• ∑ = {0, 1},
• q₀ = {a},
• F = {c}, and

Transition function δ as shown by the following table −

Present State	Next State for Input 0	Next State for Input 1
a	a	b
b	c	a
c	b	c

Its graphical representation would be as follows −