Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is internal chip organization in computer architecture?
The internal organization is linear. This chip has three address inputs and two data outputs, and 16 bits of internal storage constructed as eight 2-bit locations. The three address bits are decoded to choose one of the eight locations, but only if the chip enable is active. If CE = 0, the decoder is disabled and no location is selected.
The tri-state buffers for that location’s cells are enabled, authorizing data to move to the output buffers. If both CE and OE are set to 1, these buffers are enabled and the data is output from the chip, therefore, the outputs are tri-stated.
As the multiple locations improve, the size of the decoder address required in a linear organization becomes prohibitively high. The memory chip can be invented using multiple dimensions of decoding. To illustrate this organization, consider the two-dimensional organization of the same 8 x 2 ROM chip shown in the figure.
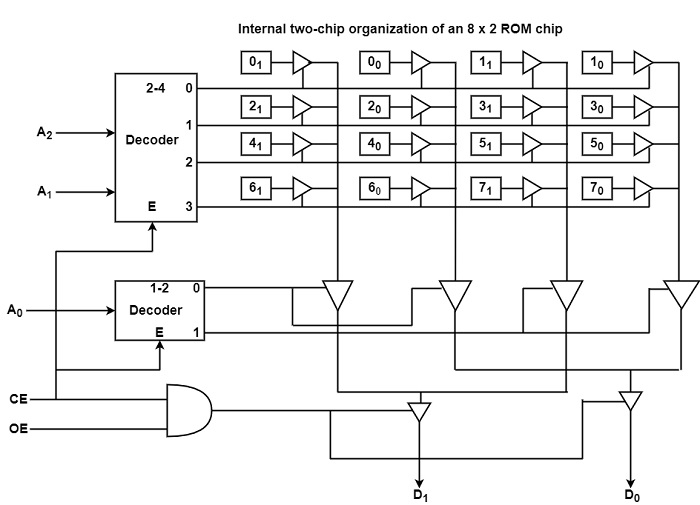
This configuration has four rows with four bits per row, each row holds two data values. For example, the first row of the ROM includes the data at addresses 0 and 1. The two high-order address bits of the two locations in each row are the same.
These two high-order address bits are chosen from one of the four rows, and the low-order address bit chooses one of the two locations in the row.
In larger memory chips, this saving can be important. Consider a 4096 x 1 chip. The linear organization will need a 12 to 4096 decoder, the size of which is proportional to the multiple outputs.
The size of an n to 2n decoder is said to be O(2n). If the chip is constructed as a 64 x 64 two-dimensional array instead, it will have two 6 to 64 decoders: one to choose one of the 64 rows and the other to choose one of the 64 cells inside the row. The size of the decoders is proportional to 2 x 64, or O (2 x 2n/2)=O$(2^ {\frac{n}{2}+1})$.
5K+ Views
