Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
What is Fixed Point Representation in Computer Architecture?
Fixed-point is an elementary and simple method to define factorial numbers. The fixed-point numbers help a constant amount of bits. The “fixed-point” defines the decimal point of a number. There is no free symbol to name where the decimal point promote. But, in binary, bits can either be 0 or 1.
Decimal Fixed-Point Representation
Fixed-point representation has a radix point known as decimal point. Fixed-point numbers having decimal points at the right end of the number are treated as integers because the fixed-point numbers having decimal points at the left end of the number are treated as fractions. In this method, the decimal point position is settled because the number saved in the memory is considered as an integer or as a fraction.
The binary numbers that are unsigned are continually considered as positive integers and are defined as 0s in the MSB. The binary numbers that are registered contrast for negative numbers and are defined as 1s in the MSB.
The magnitude of the signed binary numbers can be described using three methods are as follows −
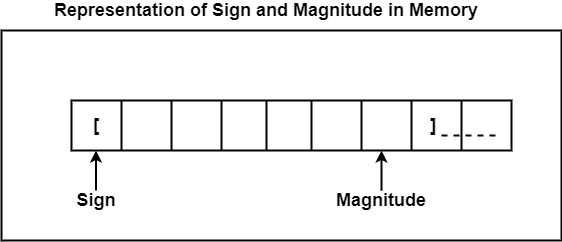
Sign and Magnitude Representation
In this method, the leftmost bit in the number is used for denoting the sign; 0 denotes a positive integer, and 1 denotes a negative integer. The remaining bits in the number provide the magnitude of the number.
Example − -2410 is defined as −
10011000
In this example, the leftmost bit 1 means negative, and the magnitude is 24.
The magnitude for both positive and negative values is equal, but they alter only with their signs.
The range of values for the sign and magnitude representation is from -127 to 127.
Signed 1’s Complement Representation
In this representation, a negative value is received by taking the 1’s complement of the equivalent positive number. It can add a signed 1’s complement method creates end carry during arithmetic operation that cannot be rejected.
The range of values for the signed 1’s complement representation is from -127 to 128.
Example − Consider 8-bit numbers for 1’s complement.
(29)10 = (00011101)2 = 0000111011’s complement for positive value
-(29)10 = -(00011101)2 = 111100010 1’s complement for negative value
Signed 2’s Complement Representation
In signed 2’s complement representation, the 2’s complement of a number is discovered by first creating the 1’s complement of that number, then incrementing the result by 1.
The range of values for the signed 2’s complement representation is from -128 to 127.
Example − Consider 8-bit numbers for 2’s complement.
(29)10= (00011100)2 = (000011100)2’s1’s complement for positive value
-(29)10 = -(00011100)2 = (11110010)2’s1’s complement for negative value
10K+ Views
To Continue Learning Please Login