Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Planar Graphs and their Properties
A graph 'G' is said to be planar if it can be drawn on a plane or a sphere so that no two edges cross each other at a non-vertex point.
Example
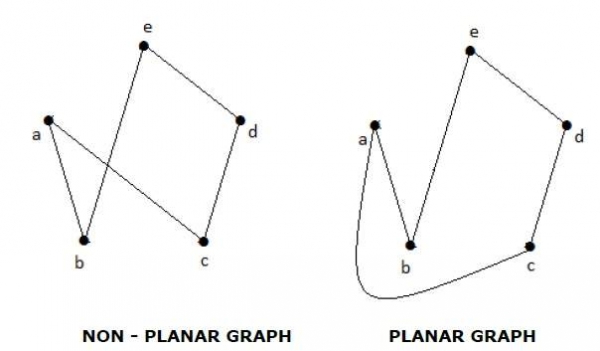
Regions
Every planar graph divides the plane into connected areas called regions.
Example
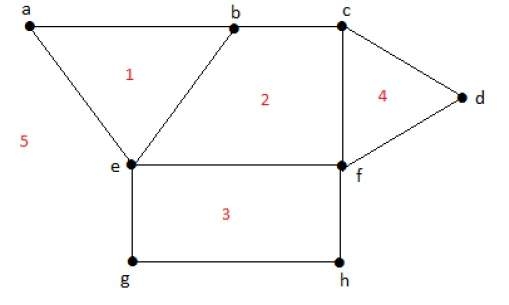
Degree of a bounded region r = deg(r) = Number of edges enclosing the regions r.
deg(1) = 3 deg(2) = 4 deg(3) = 4 deg(4) = 3 deg(5) = 8
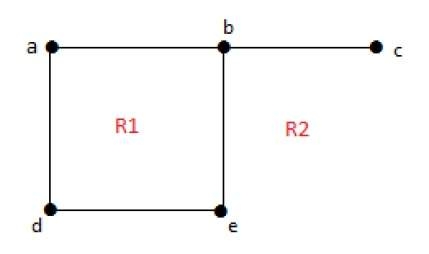
Degree of an unbounded region r = deg(r) = Number of edges enclosing the regions r.
deg(R1) = 4 deg(R2) = 6
In planar graphs, the following properties hold good −
1. In a planar graph with 'n' vertices, sum of degrees of all the vertices is
n ∑ i=1 deg(Vi) = 2|E|2. According to Sum of Degrees of Regions Theorem, in a planar graph with 'n' regions, Sum of degrees of regions is −
n ∑ i=1 deg(ri) = 2|E|
Based on the above theorem, you can draw the following conclusions −
In a planar graph,
If degree of each region is K, then the sum of degrees of regions is
K|R| = 2|E|
If the degree of each region is at least K(≥ K), then
K|R| ≤ 2|E|
If the degree of each region is at most K(≤ K), then
K|R| ≥ 2|E|
Note − Assume that all the regions have same degree.
3. According to Euler's Formulae on planar graphs,
If a graph 'G' is a connected planar, then
|V| + |R| = |E| + 2
If a planar graph with 'K' components then
|V| + |R|=|E| + (K+1)
Where, |V| is the number of vertices, |E| is the number of edges, and |R| is the number of regions.
4. Edge Vertex Inequality
If 'G' is a connected planar graph with degree of each region at least 'K' then,
|E| ≤ k/k - 2{|v|-2}
You know, |V| + |R| = |E| + 2
K.|R| ≤ 2|E|
K(|E| - |V| + 2) ≤ 2|E|
(K - 2)|E| ≤ K(|V| - 2)
|E| ≤ k/k - 2{|v| - 2}
5. If 'G' is a simple connected planar graph, then
|E| ≤ 3|V| − 6 |R| ≤ 2|V| − 4
There exists at least one vertex V ∈ G, such that deg(V) ≤ 5
6. If 'G' is a simple connected planar graph (with at least 2 edges) and no triangles, then
|E| ≤ {2|V| – 4}7. Kuratowski's Theorem
A graph 'G' is non-planar if and only if 'G' has a subgraph which is homeomorphic to K5 or K3,3.
5K+ Views
