Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Eulerian Graphs
Euler Graph - A connected graph G is called an Euler graph, if there is a closed trail which includes every edge of the graph G.
Euler Path - An Euler path is a path that uses every edge of a graph exactly once. An Euler path starts and ends at different vertices.
Euler Circuit - An Euler circuit is a circuit that uses every edge of a graph exactly once. An Euler circuit always starts and ends at the same vertex. A connected graph G is an Euler graph if and only if all vertices of G are of even degree, and a connected graph G is Eulerian if and only if its edge set can be decomposed into cycles.
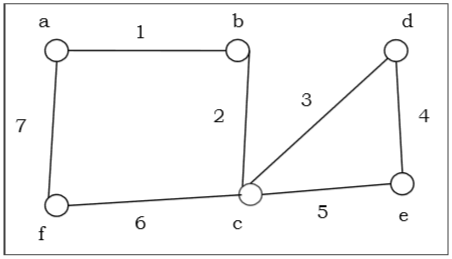
The above graph is an Euler graph as a 1 b 2 c 3 d 4 e 5 c 6 f 7 g covers all the edges of the graph.
Non-Euler Graph
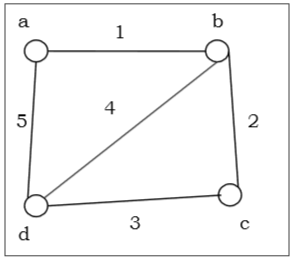
Here degree of vertex b and d is 3, an odd degree and violating the euler graph condition.
20K+ Views
