Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Eulerian and Hamiltonian Graphs in Data Structure
In this section we will see the Eulerian and Hamiltonian Graphs. But before diving into that, at first we have to see what are trails in graph. Suppose we have one graph like below −
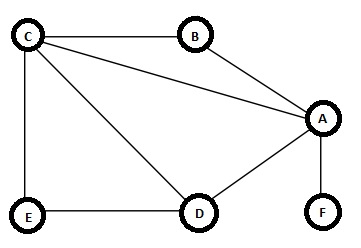
The trail is a path, which is a sequence of edges (v1, v2), (v2, v3), …, (vk - 1, vk) in which all vertices (v1, v2, … , vk) may not be distinct, but all edges are distinct. In this example one trail is {(B, A), (A, C), (C, D), (D, A), (A, F)} This is a trail. But this will not be considered as simple path as vertex A is visited twice. If the first and the last vertices are same, then that will be a closed trail.
Eulerian Trail
The Eulerian Trail in a graph G(V, E) is a trail, that includes every edge exactly once. If G has closed Eulerian Trail, then that graph is called Eulerian Graph. In other words, we can say that a graph G will be Eulerian graph, if starting from one vertex, we can traverse every edge exactly once and return to the starting vertex. Euler proved that a graph is called the Eulerian graph if and only if the degree of its every vertex is even.
Hamiltonian Cycle
One cycle is called as Hamiltonian cycle if it passes through every vertex of the graph G. There are many different theorems that give sufficient conditions for a graph to be Hamiltonian. However, the problem determining if an arbitrary graph is Hamiltonian is NPComplete problem.
1K+ Views
