Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Graphs and its traversal algorithms
In this section we will see what is a graph data structure, and the traversal algorithms of it.
The graph is one non-linear data structure. That is consists of some nodes and their connected edges. The edges may be director or undirected. This graph can be represented as G(V, E). The following graph can be represented as G({A, B, C, D, E}, {(A, B), (B, D), (D, E), (B, C), (C, A)})
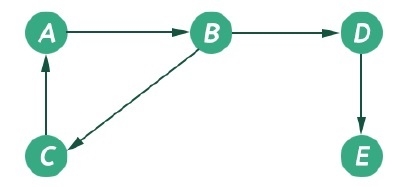
The graph has two types of traversal algorithms. These are called the Breadth First Search and Depth First Search.
Breadth First Search (BFS)
The Breadth First Search (BFS) traversal is an algorithm, which is used to visit all of the nodes of a given graph. In this traversal algorithm one node is selected and then all of the adjacent nodes are visited one by one. After completing all of the adjacent vertices, it moves further to check another vertices and checks its adjacent vertices again.
Algorithm
bfs(vertices, start) Input: The list of vertices, and the start vertex. Output: Traverse all of the nodes, if the graph is connected. Begin define an empty queue que at first mark all nodes status as unvisited add the start vertex into the que while que is not empty, do delete item from que and set to u display the vertex u for all vertices 1 adjacent with u, do if vertices[i] is unvisited, then mark vertices[i] as temporarily visited add v into the queue mark done mark u as completely visited done End
Depth First Search (DFS)
The Depth First Search (DFS) is a graph traversal algorithm. In this algorithm one starting vertex is given, and when an adjacent vertex is found, it moves to that adjacent vertex first and try to traverse in the same manner.
Algorithm
dfs(vertices, start) Input: The list of all vertices, and the start node. Output: Traverse all nodes in the graph. Begin initially make the state to unvisited for all nodes push start into the stack while stack is not empty, do pop element from stack and set to u display the node u if u is not visited, then mark u as visited for all nodes i connected to u, do if ith vertex is unvisited, then push ith vertex into the stack mark ith vertex as visited done done End
38K+ Views
