Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Adjacency Matrices and their properties
Adjacency Matrix
Adjacency Matrix is used to represent a graph. We can represent directed as well as undirected graphs using adjacency matrices. Following are the key properties of an Adjacency matrix.
Properties
An Adjacency Matrix A[V][V] is a 2D array of size V × V where V is the number of vertices in a undirected graph.
If there is an edge between Vx to Vy then the value of A[Vx][Vy] = 1 and A[Vy][Vx]=1, otherwise the value will be zero.
For a directed graph, if there is an edge between Vx to Vy, then the value of A[Vx][Vy]=1, otherwise the value will be zero.
Adjacency Matrix of an Undirected Graph
Let us consider the following undirected graph and construct the adjacency matrix −
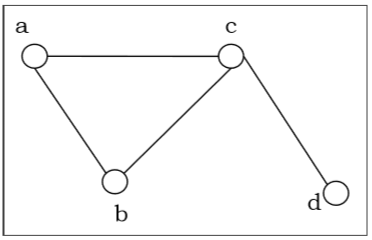
Adjacency matrix of the above undirected graph will be −
| a | b | c | d | |
| a | 0 | 1 | 1 | 0 |
| b | 1 | 0 | 1 | 0 |
| c | 1 | 1 | 0 | 1 |
| d | 0 | 0 | 1 | 0 |
Adjacency Matrix of a Directed Graph
Let us consider the following directed graph and construct its adjacency matrix −
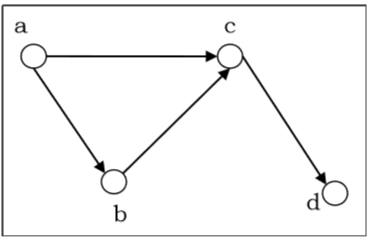
Adjacency matrix of the above directed graph will be −
| a | b | c | d | |
| a | 0 | 1 | 1 | 0 |
| b | 0 | 0 | 1 | 0 |
| c | 0 | 0 | 0 | 1 |
| d | 0 | 0 | 0 | 0 |
2K+ Views
To Continue Learning Please Login