Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Isomorphism and Homeomorphism of graphs
Isomorphism
If two graphs G and H contain the same number of vertices connected in the same way, they are called isomorphic graphs (denoted by G ≅ H).
It is easier to check non-isomorphism than isomorphism. If any of these following conditions occurs, then two graphs are non-isomorphic −
- The number of connected components are different
- Vertex-set cardinalities are different
- Edge-set cardinalities are different
- Degree sequences are different
Example
The following graphs are isomorphic −
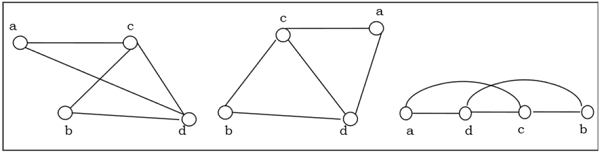
Homomorphism
A homomorphism from a graph G to a graph H is a mapping (May not be a bijective mapping) h: G → H such that − (x, y) ∈ E(G) → (h(x), h(y)) ∈ E(H). It maps adjacent vertices of graph G to the adjacent vertices of the graph H.
Properties of Homomorphisms
A homomorphism is an isomorphism if it is a bijective mapping.
Homomorphism always preserves edges and connectedness of a graph.
The compositions of homomorphisms are also homomorphisms.
To find out if there exists any homomorphic graph of another graph is a NPcomplete problem.
6K+ Views
