- Trending Categories
Data Structure
Networking
RDBMS
Operating System
Java
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Hamiltonian Graphs
Hamiltonian graph - A connected graph G is called Hamiltonian graph if there is a cycle which includes every vertex of G and the cycle is called Hamiltonian cycle. Hamiltonian walk in graph G is a walk that passes through each vertex exactly once.
Dirac's Theorem - If G is a simple graph with n vertices, where n ≥ 3 If deg(v) ≥ {n}/{2} for each vertex v, then the graph G is Hamiltonian graph.
Ore's Theorem - If G is a simple graph with n vertices, where n ≥ 2 if deg(x) + deg(y) ≥ n for each pair of non-adjacent vertices x and y, then the graph G is Hamiltonian graph.
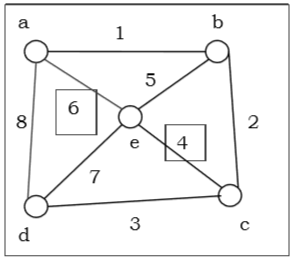
In above example, sum of degree of a and c vertices is 6 and is greater than total vertices, 5 using Ore's theorem, it is an Hamiltonian Graph.
Non-Hamiltonian Graph
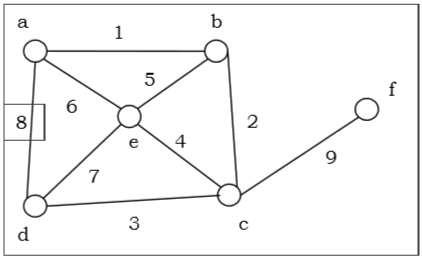
In above example, sum of degree of a and f vertices is 4 and is less than total vertices, 4 using Ore's theorem, it is not an Hamiltonian Graph.
- Related Questions & Answers
- Eulerian and Hamiltonian Graphs in Data Structure
- Hamiltonian Cycle
- Euler and Hamiltonian Paths
- Bipartite Graphs
- Eulerian Graphs
- Planar Graphs
- Strongly Connected Graphs
- Representation of Graphs
- Basic Concepts of Graphs
- Connected vs Disconnected Graphs
- Matrix Representation of Graphs
- Planar Graphs and their Properties
- Graphs and its traversal algorithms
- Isomorphism and Homeomorphism of graphs
- Displaying bar graphs using Matplotlib