Modeling Multiplication of Proper Fractions Online Quiz

Following quiz provides Multiple Choice Questions (MCQs) related to Modeling Multiplication of Proper Fractions. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

Q 1 - Multiply the fractions using an area model$\frac{1}{5}$ ×$\frac{1}{3}$

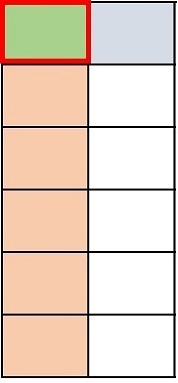
Answer : A

Explanation

Step 1:

In this problem, we want to find $\frac{1}{5}$ of $\frac{1}{3}$

Step 2:

First we divide the height of a rectangle into 3 equal parts. We shade one part to represent $\frac{1}{3}$

Step 3:

Next we divide the width into 5 equal parts and shade 1 part to make it $\frac{1}{5}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 15 parts in total and 1 of the parts overlaps.

Step 5:

So, the product is $\frac{1}{5}$ ×$\frac{1}{3}$ = $\frac{1}{15}$

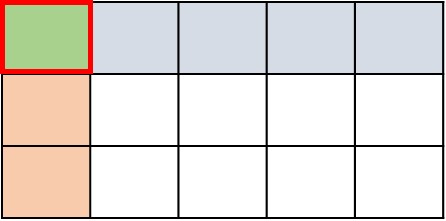
modeling of Multiplication of Proper Fractions

Q 2 - Multiply the fractions using an area model $\frac{1}{5}$ × $\frac{1}{4}$

Answer : C

Explanation

Step 1:

In this problem, we want to find $\frac{1}{5}$ of $\frac{1}{4}$

Step 2:

First we divide the height of a rectangle into 4 equal parts. We shade one part to represent $\frac{1}{4}$

Step 3:

Next we divide the width into 5 equal parts and shade 1 part to make it $\frac{1}{5}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 20 parts in total and one of the parts overlaps.

Step 5:

So, the product is $\frac{1}{5}$ × $\frac{1}{4}$ = $\frac{1}{20}$

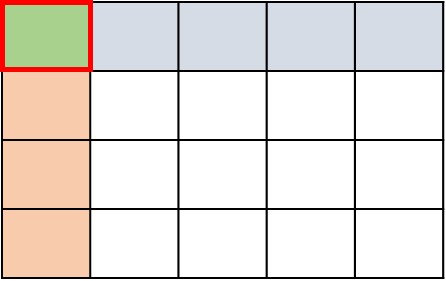
Q 3 - Multiply the fractions using an area model $\frac{1}{5}$ × $\frac{1}{6}$

Answer : B

Explanation

Step 1:

In this problem, we want to find $\frac{1}{5}$ of $\frac{1}{6}$

Step 2:

First we divide the height of a rectangle into 6 equal parts. We shade one part to represent $\frac{1}{6}$

Step 3:

Next we divide the width into 5 equal parts and shade 1 part to make it $\frac{1}{5}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 30 equal parts in total and one of the parts overlaps.

Step 5:

So, the product is $\frac{1}{5}$ × $\frac{1}{6}$ = $\frac{1}{30}$

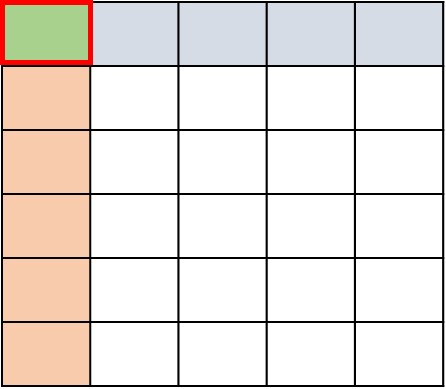
Q 4 - Multiply the fractions using an area model $\frac{1}{2}$ × $\frac{1}{4}$

Answer : D

Explanation

Step 1:

In this problem, we want to find $\frac{1}{2}$ of $\frac{1}{4}$

Step 2:

First we divide the height of a rectangle into 4 equal parts. We shade one part to represent $\frac{1}{4}$

Step 3:

Next we divide the width into 2 equal parts and shade 1 part to make it $\frac{1}{2}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 8 parts in total and one of the parts overlaps.

Step 5:

So, the product is $\frac{1}{2}$ × $\frac{1}{4}$ = $\frac{1}{8}$

Q 5 - Multiply the fractions using an area model $\frac{2}{5}$ × $\frac{1}{2}$

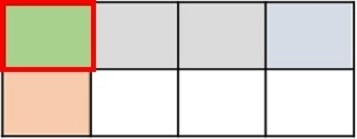
Answer : C

Explanation

Step 1:

In this problem, we want to find $\frac{2}{5}$ of $\frac{1}{2}$

Step 2:

First we divide the height of a rectangle into 2 equal parts. We shade one part to represent $\frac{1}{2}$.

Step 3:

Next we divide the width into 5 equal parts and shade 2 parts to make it $\frac{2}{5}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 10 parts in total and two of the parts overlap.

Step 5:

So, the product is $\frac{2}{5}$ × $\frac{1}{2}$ = $\frac{2}{10}$

Q 6 - Multiply the fractions using an area model $\frac{2}{3}$ × $\frac{1}{2}$

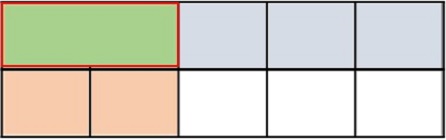
Answer : A

Explanation

Step 1:

In this problem, we want to find $\frac{2}{3}$ of $\frac{1}{2}$

Step 2:

First we divide the height of a rectangle into 2 equal parts. We shade one part to represent $\frac{1}{2}$.

Step 3:

Next we divide the width into 3 equal parts and shade 2 parts to make it $\frac{2}{3}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 6 parts in total and two of the parts overlap.

Step 5:

So, the product is $\frac{2}{3}$ × $\frac{1}{2}$ = $\frac{2}{6}$

Q 7 - Multiply the fractions using an area model $\frac{1}{2}$ × $\frac{1}{2}$

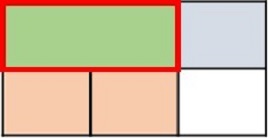
Answer : B

Explanation

Step 1:

In this problem, we want to find $\frac{1}{2}$ of $\frac{1}{2}$

Step 2:

First we divide the height of a rectangle into 2 equal parts. We shade one part to represent $\frac{1}{2}$

Step 3:

Next we divide the width into 2 equal parts and shade 1 part to make it $\frac{1}{2}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 4 parts in total and one of the parts overlaps.

Step 5:

So, the product is $\frac{1}{2}$ × $\frac{1}{2}$ = $\frac{1}{4}$

Q 8 - Multiply the fractions using an area model $\frac{2}{3}$ × $\frac{1}{6}$

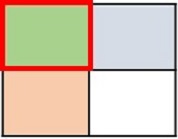
Answer : D

Explanation

Step 1:

In this problem, we want to find $\frac{2}{3}$ of $\frac{1}{6}$

Step 2:

First we divide the height of a rectangle into 6 equal parts. We shade one part to represent $\frac{1}{6}$

Step 3:

Next we divide the width into 3 equal parts and shade 2 parts to make it $\frac{2}{3}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 18 parts in total and two of the parts overlap.

Step 5:

So, the product is $\frac{2}{3}$ × $\frac{1}{6}$ = $\frac{2}{18}$

Q 9 - Multiply the fractions using an area model $\frac{3}{4}$ × $\frac{1}{2}$

Answer : B

Explanation

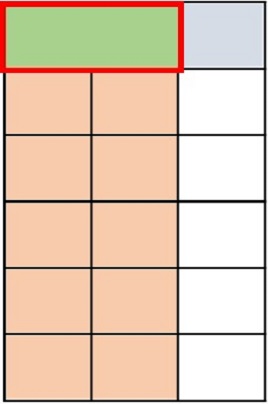
Step 1:

In this problem, we want to find $\frac{3}{4}$ of $\frac{1}{2}$

Step 2:

First we divide the height of a rectangle into 2 equal parts. We shade one part to represent $\frac{1}{2}$

Step 3:

Next we divide the width into 4 equal parts and shade 3 parts to make it $\frac{3}{4}$.

Step 4:

Step 5:

So, the product is $\frac{3}{4}$ × $\frac{1}{2}$ = $\frac{3}{8}$

Q 10 - Multiply the fractions using an area model $\frac{1}{2}$ × $\frac{1}{6}$

Answer : C

Explanation

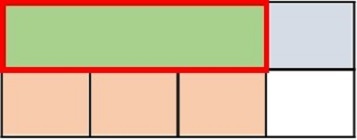
Step 1:

In this problem, we want to find $\frac{1}{2}$ of $\frac{1}{6}$

Step 2:

First we divide the height of a rectangle into 6 equal parts. We shade one part to represent $\frac{1}{6}$

Step 3:

Next we divide the width into 2 equal parts and shade 1 part to make it $\frac{1}{2}$.

Step 4:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 12 parts in total and one of the parts overlaps.

Step 5:

So, the product is $\frac{1}{2}$ × $\frac{1}{6}$ = $\frac{1}{12}$

modeling_multiplication_of_proper_fractions.htm