- Multiply and Divide Fractions
- Home
- Product of a Unit Fraction and a Whole Number
- Product of a Fraction and a Whole Number: Problem Type 1
- Introduction to Fraction Multiplication
- Fraction Multiplication
- Product of a Fraction and a Whole Number Problem Type 2
- Determining if a Quantity is Increased or Decreased When Multiplied by a Fraction
- Modeling Multiplication of Proper Fractions
- Multiplication of 3 Fractions
- Word Problem Involving Fractions and Multiplication
- The Reciprocal of a Number
- Division Involving a Whole Number and a Fraction
- Fraction Division
- Fact Families for Multiplication and Division of Fractions
- Modeling Division of a Whole Number by a Fraction
- Word Problem Involving Fractions and Division
Modeling Division of a Whole Number by a Fraction
Introduction
Here, in this lesson, we learn how to use area model to divide a whole number by a fraction. There is a whole number and a fraction that divides that whole number. We consider a whole number as that many squares as the number indicates.We divide each of the squares into that many parts as the denominator of the fraction indicates. We find the result of this division by counting the total number of parts of the squares.
Example
Divide 3 ÷ $\frac{1}{2}$ using an area model.
Solution
Step 1:
The whole number 3 is taken as three squares. As the fraction is one-half, each of the squares is divided into two halves.
Step 2:
Now the halves in all three squares are counted and found to be 6. This is the answer we get by dividing 3 by $\frac{1}{2}$.
So, 3 ÷ $\frac{1}{2}$ = 6
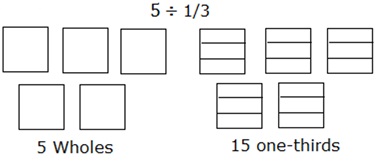
Problem 1
Divide 5 ÷ $\frac{1}{3}$ using an area model.
Solution
Step 1:
Dividing 5 into one-thirds can be modeled as follows:
Consider 5 squares as 5 wholes. Each of the squares is further divided into three parts or one-thirds.
Step 2:
Then counting the total number of such parts of the squares or wholes gives the answer which is 15.
So, 5 ÷ $\frac{1}{3}$ = 15
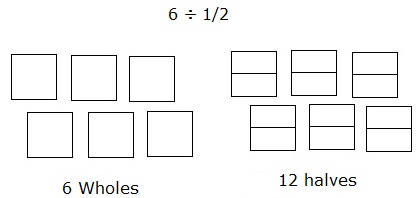
Problem 2
Divide 6 ÷ $\frac{1}{2}$ using an area model.
Solution
Step 1:
Dividing 6 into one-halves can be modeled as follows:
Consider 6 squares as 6 wholes. Each of the squares is further divided into two parts or one-halves.
Step 2:
Then counting the total number of such parts of the squares or wholes gives the answer which is 12.
So, 6 ÷ $\frac{1}{2}$ = 12