Modeling Multiplication of Proper Fractions

Let’s use an area model to multiply fractions. The area model gives us a good picture of what happens when we multiply two fractions. We see the problem in two dimensions. We represent the height using one fraction and the width using another fraction. It is important to see this kind of connections in mathematics.

Multiply the fractions using an area model $\frac{1}{3}$ × $\frac{1}{3}$

Solution

Step 1:

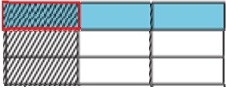
In this problem, we want to find $\frac{1}{3}$ of $\frac{1}{3}$

Step 2:

First we divide the height of a rectangle into 3 equal parts.

Step 3:

We shade one part to represent $\frac{1}{3}$

Step 4:

Next we divide the width into 3 equal parts and shade 1 part to make it $\frac{1}{3}$

Step 5:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 9 total parts and 1 of the parts overlaps.

Step 6:

So, the product is $\frac{1}{9}$.

$\frac{1}{3}$ × $\frac{1}{3}$ = $\frac{1}{9}$

Multiply the fractions using an area model $\frac{2}{3}$ × $\frac{1}{3}$

Solution

Step 1:

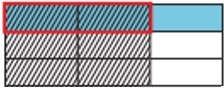
In this problem, we want to find $\frac{2}{3}$ of $\frac{1}{3}$

Step 2:

First we divide the height of a rectangle into 3 equal parts.

Step 3:

We shade one part to represent $\frac{1}{3}$

Step 4:

Next we divide the width into 3 equal parts and shade 2 parts to make it $\frac{2}{3}$

Step 5:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 9 total parts and 2 of the parts overlaps.

Step 6:

So, the product is $\frac{2}{9}$.

$\frac{2}{3}$ × $\frac{1}{3}$ = $\frac{2}{9}$

Multiply the fractions using an area model $\frac{1}{2}$ × $\frac{1}{3}$

Solution

Step 1:

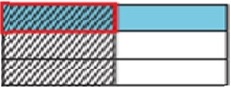
In this problem, we want to find $\frac{1}{2}$ of $\frac{1}{3}$

Step 2:

First we divide the height of a rectangle into 3 equal parts.

Step 3:

We shade one part to represent $\frac{1}{3}$

Step 4:

Next we divide the width into 2 equal parts and shade 1 part to make it $\frac{1}{2}$

Step 5:

Now we can figure out the product. The part where the shading overlaps represents the numerator. The total number of parts represents the denominator. There are 6 total parts and 1 of the parts overlaps.

Step 6:

So, the product is $\frac{1}{6}$.

$\frac{1}{2}$ × $\frac{1}{3}$ = $\frac{1}{6}$