
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Array Data Structure
What is an Array?
An array is a type of linear data structure that is defined as a collection of elements with same or different data types. They exist in both single dimension and multiple dimensions. These data structures come into picture when there is a necessity to store multiple elements of similar nature together at one place.
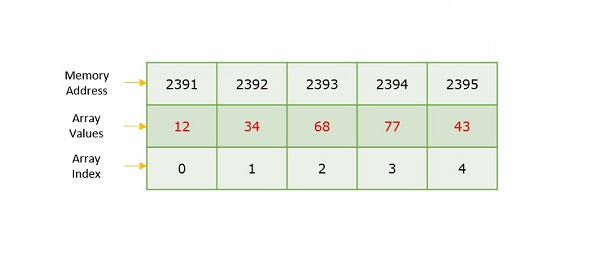
The difference between an array index and a memory address is that the array index acts like a key value to label the elements in the array. However, a memory address is the starting address of free memory available.
Following are the important terms to understand the concept of Array.
Element − Each item stored in an array is called an element.
Index − Each location of an element in an array has a numerical index, which is used to identify the element.
Syntax
Creating an array in C and C++ programming languages −
data_type array_name[array_size]={elements separated by commas}
or,
data_type array_name[array_size];
Creating an array in Java programming language −
data_type[] array_name = {elements separated by commas}
or,
data_type array_name = new data_type[array_size];
Need for Arrays
Arrays are used as solutions to many problems from the small sorting problems to more complex problems like travelling salesperson problem. There are many data structures other than arrays that provide efficient time and space complexity for these problems, so what makes using arrays better? The answer lies in the random access lookup time.
Arrays provide O(1) random access lookup time. That means, accessing the 1st index of the array and the 1000th index of the array will both take the same time. This is due to the fact that array comes with a pointer and an offset value. The pointer points to the right location of the memory and the offset value shows how far to look in the said memory.
array_name[index]
| |
Pointer Offset
Therefore, in an array with 6 elements, to access the 1st element, array is pointed towards the 0th index. Similarly, to access the 6th element, array is pointed towards the 5th index.
Array Representation
Arrays are represented as a collection of buckets where each bucket stores one element. These buckets are indexed from '0' to 'n-1', where n is the size of that particular array. For example, an array with size 10 will have buckets indexed from 0 to 9.
This indexing will be similar for the multidimensional arrays as well. If it is a 2-dimensional array, it will have sub-buckets in each bucket. Then it will be indexed as array_name[m][n], where m and n are the sizes of each level in the array.
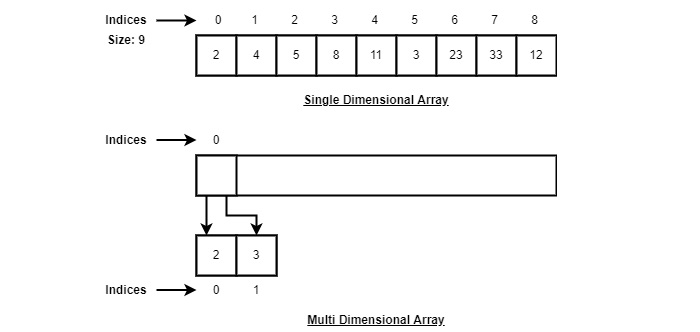
As per the above illustration, following are the important points to be considered.
Index starts with 0.
Array length is 9 which means it can store 9 elements.
Each element can be accessed via its index. For example, we can fetch an element at index 6 as 23.
Basic Operations in Arrays
The basic operations in the Arrays are insertion, deletion, searching, display, traverse, and update. These operations are usually performed to either modify the data in the array or to report the status of the array.
Following are the basic operations supported by an array.
Traverse − print all the array elements one by one.
Insertion − Adds an element at the given index.
Deletion − Deletes an element at the given index.
Search − Searches an element using the given index or by the value.
Update − Updates an element at the given index.
Display − Displays the contents of the array.
In C, when an array is initialized with size, then it assigns defaults values to its elements in following order.
| Data Type | Default Value |
|---|---|
| bool | false |
| char | 0 |
| int | 0 |
| float | 0.0 |
| double | 0.0f |
| void | |
| wchar_t | 0 |
Array - Insertion Operation
In the insertion operation, we are adding one or more elements to the array. Based on the requirement, a new element can be added at the beginning, end, or any given index of array. This is done using input statements of the programming languages.
Algorithm
Following is an algorithm to insert elements into a Linear Array until we reach the end of the array −
1. Start 2. Create an Array of a desired datatype and size. 3. Initialize a variable 'i' as 0. 4. Enter the element at ith index of the array. 5. Increment i by 1. 6. Repeat Steps 4 & 5 until the end of the array. 7. Stop
Example
Here, we see a practical implementation of insertion operation, where we add data at the end of the array −
#include <stdio.h>
int main(){
int LA[3] = {}, i;
printf("Array Before Insertion:\n");
for(i = 0; i < 3; i++)
printf("LA[%d] = %d \n", i, LA[i]);
printf("Inserting Elements.. \n");
printf("The array elements after insertion :\n"); // prints array values
for(i = 0; i < 3; i++) {
LA[i] = i + 2;
printf("LA[%d] = %d \n", i, LA[i]);
}
return 0;
}
#include <iostream>
using namespace std;
int main(){
int LA[3] = {}, i;
cout << "Array Before Insertion:" << endl;
for(i = 0; i < 3; i++)
cout << "LA[" << i <<"] = " << LA[i] << endl;
//prints garbage values
cout << "Inserting elements.." <<endl;
cout << "Array After Insertion:" << endl; // prints array values
for(i = 0; i < 5; i++) {
LA[i] = i + 2;
cout << "LA[" << i <<"] = " << LA[i] << endl;
}
return 0;
}
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[3];
System.out.println("Array Before Insertion:");
for(int i = 0; i < 3; i++)
System.out.println("LA[" + i + "] = " + LA[i]); //prints empty array
System.out.println("Inserting Elements..");
// Printing Array after Insertion
System.out.println("Array After Insertion:");
for(int i = 0; i < 3; i++) {
LA[i] = i+3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
# python program to insert element using insert operation
def insert(arr, element):
arr.append(element)
# Driver's code
if __name__ == '__main__':
# declaring array and value to insert
LA = [0, 0, 0]
x = 0
# array before inserting an element
print("Array Before Insertion: ")
for x in range(len(LA)):
print("LA", [x], " = " , LA[x])
print("Inserting elements....")
# array after Inserting element
for x in range(len(LA)):
LA.append(x);
LA[x] = x+1;
print("Array After Insertion: ")
for x in range(len(LA)):
print("LA", [x], " = " , LA[x])
Output
Array Before Insertion: LA[0] = 0 LA[1] = 0 LA[2] = 0 Inserting elements.. Array After Insertion: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 5 LA[4] = 6
For other variations of array insertion operation, click here.
Array - Deletion Operation
In this array operation, we delete an element from the particular index of an array. This deletion operation takes place as we assign the value in the consequent index to the current index.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to delete an element available at the Kth position of LA.
1. Start 2. Set J = K 3. Repeat steps 4 and 5 while J < N 4. Set LA[J] = LA[J + 1] 5. Set J = J+1 6. Set N = N-1 7. Stop
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
void main(){
int LA[] = {1,3,5};
int n = 3;
int i;
printf("The original array elements are :\n");
for(i = 0; i<n; i++)
printf("LA[%d] = %d \n", i, LA[i]);
for(i = 1; i<n; i++) {
LA[i] = LA[i+1];
n = n - 1;
}
printf("The array elements after deletion :\n");
for(i = 0; i<n; i++)
printf("LA[%d] = %d \n", i, LA[i]);
}
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5};
int i, n = 3;
cout << "The original array elements are :"<<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] << endl;
}
for(i = 1; i<n; i++) {
LA[i] = LA[i+1];
n = n - 1;
}
cout << "The array elements after deletion :"<<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] <<endl;
}
}
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[3];
int n = LA.length;
System.out.println("Array Before Deletion:");
for(int i = 0; i < n; i++) {
LA[i] = i + 3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
for(int i = 1; i<n-1; i++) {
LA[i] = LA[i+1];
n = n - 1;
}
System.out.println("Array After Deletion:");
for(int i = 0; i < n; i++) {
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
#python program to delete the value using delete operation
if __name__ == '__main__':
# Declaring array and deleting value
LA = [0,0,0]
n = len(LA)
print("Array Before Deletion: ")
for x in range(len(LA)):
LA.append(x)
LA[x] = x + 3
print("LA", [x], " = " , LA[x])
# delete the value if exists
# or show error it does not exist in the list
for x in range(1, n-1):
LA[x] = LA[x+1]
n = n-1
print("Array After Deletion: ")
for x in range(n):
print("LA", [x], " = " , LA[x])
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 The array elements after deletion : LA[0] = 1 LA[1] = 5
Array - Search Operation
Searching an element in the array using a key; The key element sequentially compares every value in the array to check if the key is present in the array or not.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to find an element with a value of ITEM using sequential search.
1. Start 2. Set J = 0 3. Repeat steps 4 and 5 while J < N 4. IF LA[J] is equal ITEM THEN GOTO STEP 6 5. Set J = J +1 6. PRINT J, ITEM 7. Stop
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
void main(){
int LA[] = {1,3,5,7,8};
int item = 5, n = 5;
int i = 0, j = 0;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
for(i = 0; i<n; i++) {
if( LA[i] == item ) {
printf("Found element %d at position %d\n", item, i+1);
}
}
}
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 5, n = 5;
int i = 0;
cout << "The original array elements are : " <<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] << endl;
}
for(i = 0; i<n; i++) {
if( LA[i] == item ) {
cout << "Found element " << item << " at position " << i+1 <<endl;
}
}
return 0;
}
public class ArrayDemo{
public static void main(String []args){
int LA[] = new int[5];
System.out.println("Array:");
for(int i = 0; i < 5; i++) {
LA[i] = i + 3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
for(int i = 0; i < 5; i++) {
if(LA[i] == 6)
System.out.println("Element " + 6 + " is found at index " + i);
}
}
}
#search operation using python
def findElement(arr, n, value):
for i in range(n):
if (arr[i] == value):
return i
# If the key is not found
return -1
# Driver's code
if __name__ == '__main__':
LA = [1,3,5,7,8]
print("Array element are: ")
for x in range(len(LA)):
print("LA", [x], " = ", LA[x])
value = 5
n = len(LA)
# element found using search operation
index = findElement(LA, n, value)
if index != -1:
print("Element", value, "Found at position = " + str(index + 1))
else:
print("Element not found")
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 Found element 5 at position 3
Array - Traversal Operation
This operation traverses through all the elements of an array. We use loop statements to carry this out.
Algorithm
Following is the algorithm to traverse through all the elements present in a Linear Array −
1 Start 2. Initialize an Array of certain size and datatype. 3. Initialize another variable i with 0. 4. Print the ith value in the array and increment i. 5. Repeat Step 4 until the end of the array is reached. 6. End
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
cout << "The original array elements are:\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
# Python code to iterate over a array using python
LA = [1, 3, 5, 7, 8]
# length of the elements
length = len(LA)
# Traversing the elements using For loop and range
# same as 'for x in range(len(array))'
print("Array elements are: ")
for x in range(length):
print("LA", [x], " = ", LA[x])
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
Array - Update Operation
Update operation refers to updating an existing element from the array at a given index.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to update an element available at the Kth position of LA.
1. Start 2. Set LA[K-1] = ITEM 3. Stop
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
void main(){
int LA[] = {1,3,5,7,8};
int k = 3, n = 5, item = 10;
int i, j;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
LA[k-1] = item;
printf("The array elements after updation :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
cout << "The original array elements are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
LA[2] = item;
cout << "The array elements after updation are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
int item = 15;
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
LA[3] = item;
System.out.println("The array elements after updation are: ");
for(int i = 0; i < 5; i++)
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
#update operation using python
#Declaring array elements
LA = [1,3,5,7,8]
#before updation
print("The original array elements are :");
for x in range(len(LA)):
print("LA", [x], " = ", LA[x])
#after updation
LA[2] = 10
print("The array elements after updation are: ")
for x in range(len(LA)):
print("LA", [x], " = ", LA[x])
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 The array elements after updation : LA[0] = 1 LA[1] = 3 LA[2] = 10 LA[3] = 7 LA[4] = 8
Array - Display Operation
This operation displays all the elements in the entire array using a print statement.
Algorithm
Consider LA is a linear array with N elements. Following is the algorithm to display an array elements.
1. Start 2. Print all the elements in the Array 3. Stop
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int main(){
int LA[] = {1,3,5,7,8};
int n = 5;
int i;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int n = 5;
int i;
cout << "The original array elements are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
#Display operation using python
#Display operation using python
#Declaring array elements
LA = [2,3,4,5,6]
#Displaying the array
print("The array elements are: ")
for x in range(len(LA)):
print("LA", [x], " = " , LA[x])
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8