
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Breadth First Search (BFS) Algorithm
Breadth First Search (BFS) Algorithm
Breadth First Search (BFS) algorithm traverses a graph in a breadthward motion to search a graph data structure for a node that meets a set of criteria. It uses a queue to remember the next vertex to start a search, when a dead end occurs in any iteration.
Breadth First Search (BFS) algorithm starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level.
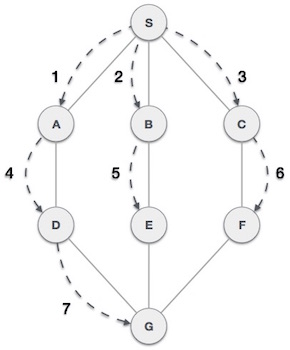
As in the example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs the following rules.
Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue.
Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.
| Step | Traversal | Description |
|---|---|---|
| 1 | 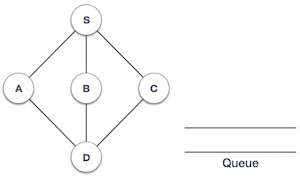 |
Initialize the queue. |
| 2 | 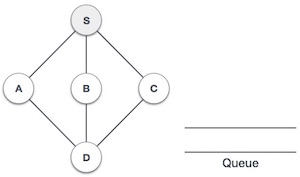 |
We start from visiting S (starting node), and mark it as visited. |
| 3 | 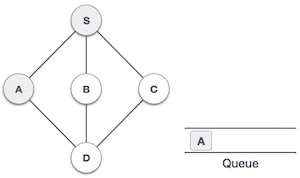 |
We then see an unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A, mark it as visited and enqueue it. |
| 4 | 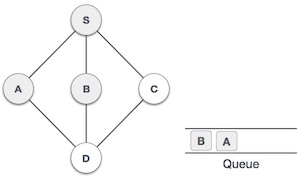 |
Next, the unvisited adjacent node from S is B. We mark it as visited and enqueue it. |
| 5 | 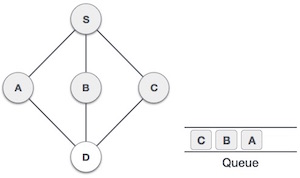 |
Next, the unvisited adjacent node from S is C. We mark it as visited and enqueue it. |
| 6 | 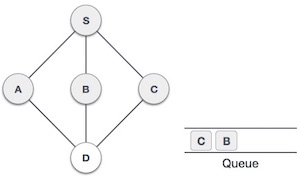 |
Now, S is left with no unvisited adjacent nodes. So, we dequeue and find A. |
| 7 | 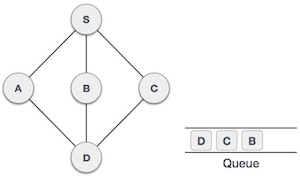 |
From A we have D as unvisited adjacent node. We mark it as visited and enqueue it. |
At this stage, we are left with no unmarked (unvisited) nodes. But as per the algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied, the program is over.
Example
Following are the implementations of Breadth First Search (BFS) Algorithm in various programming languages −
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Vertex {
char label;
bool visited;
};
//queue variables
int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//queue functions
void insert(int data) {
queue[++rear] = data;
queueItemCount++;
}
int removeData() {
queueItemCount--;
return queue[front++];
}
bool isQueueEmpty() {
return queueItemCount == 0;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
printf("%c ",lstVertices[vertexIndex]->label);
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
int i;
for(i = 0; i<vertexCount; i++) {
if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
return i;
}
return -1;
}
void breadthFirstSearch() {
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//insert vertex index in queue
insert(0);
int unvisitedVertex;
while(!isQueueEmpty()) {
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = removeData();
//no adjacent vertex found
while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(i = 0;i<vertexCount;i++) {
lstVertices[i]->visited = false;
}
}
int main() {
int i, j;
for(i = 0; i<MAX; i++) { // set adjacency
for(j = 0; j<MAX; j++) // matrix to 0
adjMatrix[i][j] = 0;
}
addVertex('S'); // 0
addVertex('A'); // 1
addVertex('B'); // 2
addVertex('C'); // 3
addVertex('D'); // 4
addEdge(0, 1); // S - A
addEdge(0, 2); // S - B
addEdge(0, 3); // S - C
addEdge(1, 4); // A - D
addEdge(2, 4); // B - D
addEdge(3, 4); // C - D
printf("\nBreadth First Search: ");
breadthFirstSearch();
return 0;
}
Output
Breadth First Search: S A B C D
//C++ code for Breadth First Traversal
#include <iostream>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Vertex {
char label;
bool visited;
};
//queue variables
int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//queue functions
void insert(int data) {
queue[++rear] = data;
queueItemCount++;
}
int removeData() {
queueItemCount--;
return queue[front++];
}
bool isQueueEmpty() {
return queueItemCount == 0;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
std::cout << lstVertices[vertexIndex]->label << " ";
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
int i;
for(i = 0; i<vertexCount; i++) {
if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
return i;
}
return -1;
}
void breadthFirstSearch() {
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//insert vertex index in queue
insert(0);
int unvisitedVertex;
while(!isQueueEmpty()) {
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = removeData();
//no adjacent vertex found
while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(i = 0;i<vertexCount;i++) {
lstVertices[i]->visited = false;
}
}
int main() {
int i, j;
for(i = 0; i<MAX; i++) { // set adjacency
for(j = 0; j<MAX; j++) // matrix to 0
adjMatrix[i][j] = 0;
}
addVertex('S'); // 0
addVertex('A'); // 1
addVertex('B'); // 2
addVertex('C'); // 3
addVertex('D'); // 4
addEdge(0, 1); // S - A
addEdge(0, 2); // S - B
addEdge(0, 3); // S - C
addEdge(1, 4); // A - D
addEdge(2, 4); // B - D
addEdge(3, 4); // C - D
std::cout << "Breadth First Search: ";
breadthFirstSearch();
return 0;
}
Output
Breadth First Search: S A B C D
//Java code for Breadth First Traversal
import java.util.LinkedList;
import java.util.Queue;
class Vertex {
char label;
boolean visited;
public Vertex(char label) {
this.label = label;
visited = false;
}
}
public class Graph {
private static final int MAX = 5;
private Vertex[] lstVertices;
private int[][] adjMatrix;
private int vertexCount;
public Graph() {
lstVertices = new Vertex[MAX];
adjMatrix = new int[MAX][MAX];
vertexCount = 0;
}
private void addVertex(char label) {
Vertex vertex = new Vertex(label);
lstVertices[vertexCount++] = vertex;
}
private void addEdge(int start, int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
private void displayVertex(int vertexIndex) {
System.out.print(lstVertices[vertexIndex].label + " ");
}
private int getAdjUnvisitedVertex(int vertexIndex) {
for (int i = 0; i < vertexCount; i++) {
if (adjMatrix[vertexIndex][i] == 1 && !lstVertices[i].visited)
return i;
}
return -1;
}
private void breadthFirstSearch() {
lstVertices[0].visited = true;
displayVertex(0);
Queue<Integer> queue = new LinkedList<>();
queue.add(0);
while (!queue.isEmpty()) {
int tempVertex = queue.poll();
int unvisitedVertex;
while ((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {
lstVertices[unvisitedVertex].visited = true;
displayVertex(unvisitedVertex);
queue.add(unvisitedVertex);
}
}
// Reset the visited flag
for (int i = 0; i < vertexCount; i++) {
lstVertices[i].visited = false;
}
}
public static void main(String[] args) {
Graph graph = new Graph();
for (int i = 0; i < MAX; i++) {
for (int j = 0; j < MAX; j++)
graph.adjMatrix[i][j] = 0;
}
graph.addVertex('S'); // 0
graph.addVertex('A'); // 1
graph.addVertex('B'); // 2
graph.addVertex('C'); // 3
graph.addVertex('D'); // 4
graph.addEdge(0, 1); // S - A
graph.addEdge(0, 2); // S - B
graph.addEdge(0, 3); // S - C
graph.addEdge(1, 4); // A - D
graph.addEdge(2, 4); // B - D
graph.addEdge(3, 4); // C - D
System.out.print("Breadth First Search: ");
graph.breadthFirstSearch();
}
}
Output
Breadth First Search: S A B C D
#Python program for Breadth First Search
# defining MAX 5
MAX = 5
class Vertex:
def __init__(self, label):
self.label = label
self.visited = False
# queue variables
queue = [0] * MAX
rear = -1
front = 0
queueItemCount = 0
# graph variables
#array of vertices
lstVertices = [None] * MAX
#adjacency matrix
adjMatrix = [[0] * MAX for _ in range(MAX)]
#vertex count
vertexCount = 0
# queue functions
def insert(data):
global rear, queueItemCount
rear += 1
queue[rear] = data
queueItemCount += 1
def removeData():
global front, queueItemCount
queueItemCount -= 1
data = queue[front]
front += 1
return data
def isQueueEmpty():
return queueItemCount == 0
# graph functions
#add vertex to the vertex list
def addVertex(label):
global vertexCount
vertex = Vertex(label)
lstVertices[vertexCount] = vertex
vertexCount += 1
#add edge to edge array
def addEdge(start, end):
adjMatrix[start][end] = 1
adjMatrix[end][start] = 1
#Display the vertex
def displayVertex(vertexIndex):
print(lstVertices[vertexIndex].label, end=" ")
#Get the adjacent unvisited vertex
def getAdjUnvisitedVertex(vertexIndex):
for i in range(vertexCount):
if adjMatrix[vertexIndex][i] == 1 and not lstVertices[i].visited:
return i
return -1
def breadthFirstSearch():
#mark first node as visited
lstVertices[0].visited = True
#Display the vertex
displayVertex(0)
#insert vertex index in queue
insert(0)
while not isQueueEmpty():
#get the unvisited vertex of vertex which is at front of the queue
tempVertex = removeData()
#no adjacent vertex found
unvisitedVertex = getAdjUnvisitedVertex(tempVertex)
while unvisitedVertex != -1:
lstVertices[unvisitedVertex].visited = True
displayVertex(unvisitedVertex)
insert(unvisitedVertex)
unvisitedVertex = getAdjUnvisitedVertex(tempVertex)
#queue is empty, search is complete, reset the visited flag
for i in range(vertexCount):
lstVertices[i].visited = False
# main function
if __name__ == "__main__":
#set adjacency
for i in range(MAX):
#matrix to 0
for j in range(MAX):
adjMatrix[i][j] = 0
addVertex('S')
addVertex('A')
addVertex('B')
addVertex('C')
addVertex('D')
addEdge(0, 1)
addEdge(0, 2)
addEdge(0, 3)
addEdge(1, 4)
addEdge(2, 4)
addEdge(3, 4)
print("Breadth First Search: ", end="")
breadthFirstSearch()
Output
Breadth First Search: S A B C D
Click to check C implementation of Breadth First Search (BFS) Algorithm
Complexity of BFS Algorithm
Time Complexity
The time complexity of the BFS algorithm is represented in the form of O(V + E), where V is the number of nodes and E is the number of edges.
Space Complexity
The space complexity of the BFS algorithm is O(V).