
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Stack Data Structure
What is a Stack?
A stack is a linear data structure where elements are stored in the LIFO (Last In First Out) principle where the last element inserted would be the first element to be deleted. A stack is an Abstract Data Type (ADT), that is popularly used in most programming languages. It is named stack because it has the similar operations as the real-world stacks, for example − a pack of cards or a pile of plates, etc.

Stack is considered a complex data structure because it uses other data structures for implementation, such as Arrays, Linked lists, etc.
Stack Representation
A stack allows all data operations at one end only. At any given time, we can only access the top element of a stack.
The following diagram depicts a stack and its operations −
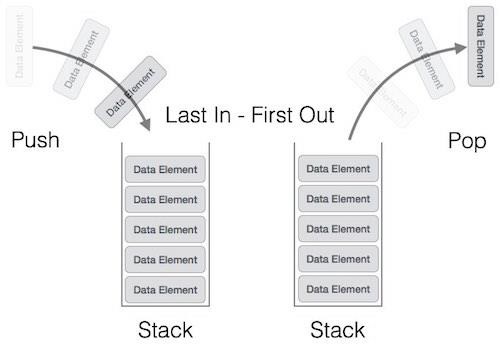
A stack can be implemented by means of Array, Structure, Pointer, and Linked List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays, which makes it a fixed size stack implementation.
Basic Operations on Stacks
Stack operations are usually performed for initialization, usage and, de-initialization of the stack ADT.
The most fundamental operations in the stack ADT include: push(), pop(), peek(), isFull(), isEmpty(). These are all built-in operations to carry out data manipulation and to check the status of the stack.
Stack uses pointers that always point to the topmost element within the stack, hence called as the top pointer.
Stack Insertion: push()
The push() is an operation that inserts elements into the stack. The following is an algorithm that describes the push() operation in a simpler way.
Algorithm
1. Checks if the stack is full.
2. If the stack is full, produces an error and exit.
3. If the stack is not full, increments top to point next
empty space.
4. Adds data element to the stack location, where top
is pointing.
5. Returns success.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full*/
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full*/
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
return data;
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0
public class Demo{
final static int MAXSIZE = 8;
static int stack[] = new int[MAXSIZE];
static int top = -1;
public static int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
public static int push(int data){
if(isfull() != 1) {
top = top + 1;
stack[top] = data;
} else {
System.out.print("Could not insert data, Stack is full.\n");
}
return data;
}
public static void main(String[] args){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
System.out.print("\nStack Elements: ");
// print stack data
for(i = 0; i < MAXSIZE; i++) {
System.out.print(stack[i] + " ");
}
}
}
Output
Stack Elements: 44 10 62 123 15 0 0 0
MAXSIZE = 8
stack = [0] * MAXSIZE
top = -1
def isfull():
if(top == MAXSIZE):
return 1
else:
return 0
def push(data):
global top
if(isfull() != 1):
top = top + 1
stack[top] = data
else:
print("Could not insert data, Stack is full.")
return data
push(44)
push(10)
push(62)
push(123)
push(15)
print("Stack Elements: ")
for i in range(MAXSIZE):
print(stack[i], end = " ")
Output
Stack Elements: 44 10 62 123 15 0 0 0
Note − In Java we have used to built-in method push() to perform this operation.
Stack Deletion: pop()
The pop() is a data manipulation operation which removes elements from the stack. The following pseudo code describes the pop() operation in a simpler way.
Algorithm
1. Checks if the stack is empty. 2. If the stack is empty, produces an error and exit. 3. If the stack is not empty, accesses the data element at which top is pointing. 4. Decreases the value of top by 1. 5. Returns success.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full*/
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to delete from the stack */
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
/*printf("Element at top of the stack: %d\n" ,peek());*/
printf("\nElements popped: \n");
// print stack data
while(!isempty()) {
int data = pop();
printf("%d ",data);
}
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Elements popped: 15 123 62 10 44
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full*/
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to delete from the stack */
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
return data;
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
return data;
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
/*printf("Element at top of the stack: %d\n" ,peek());*/
printf("\nElements popped: \n");
// print stack data
while(!isempty()) {
int data = pop();
printf("%d ",data);
}
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Elements popped: 15 123 62 10 44
public class Demo{
final static int MAXSIZE = 8;
public static int stack[] = new int[MAXSIZE];
public static int top = -1;
/* Check if the stack is empty */
public static int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full*/
public static int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to delete from the stack */
public static int pop(){
int data = 0;
if(isempty() != 1) {
data = stack[top];
top = top - 1;
return data;
} else {
System.out.print("Could not retrieve data, Stack is empty.");
}
return data;
}
/* Function to insert into the stack */
public static int push(int data){
if(isfull() != 1) {
top = top + 1;
stack[top] = data;
} else {
System.out.print("\nCould not insert data, Stack is full.\n");
}
return data;
}
/* Main function */
public static void main(String[] args){
push(44);
push(10);
push(62);
push(123);
push(15);
System.out.print("Stack Elements: ");
// print stack data
for(int i = 0; i < MAXSIZE; i++) {
System.out.print(stack[i] + " ");
}
/*printf("Element at top of the stack: %d\n" ,peek());*/
System.out.print("\nElements popped: ");
// print stack data
while(isempty() != 1) {
int data = pop();
System.out.print(data + " ");
}
}
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Elements popped: 15 123 62 10 44
MAXSIZE = 8
stack = [0] * MAXSIZE
top = -1
def isempty():
if(top == -1):
return 1
else:
return 0
def isfull():
if(top == MAXSIZE):
return 1
else:
return 0
def pop():
global top
data = 0
if(isempty() != 1):
data = stack[top]
top = top - 1
return data
else:
print("Could not retrieve data, Stack is empty.")
return data
def push(data):
global top
if(isfull() != 1):
top = top + 1
stack[top] = data
else:
print("\nCould not insert data, Stack is full.")
return data
push(44);
push(10);
push(62);
push(123);
push(15);
print("Stack Elements: ")
for i in range (MAXSIZE):
print(stack[i], end = " ")
print("\nElements popped: ")
while(isempty() != 1):
data = pop()
print(data, end = " ")
Output
Stack Elements: 44 10 62 123 15 0 0 0 Elements popped: 15 123 62 10 44
Note − In Java we are using the built-in method pop().
Retrieving topmost Element from Stack: peek()
The peek() is an operation retrieves the topmost element within the stack, without deleting it. This operation is used to check the status of the stack with the help of the top pointer.
Algorithm
1. START 2. return the element at the top of the stack 3. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
int peek(){
return stack[top];
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
printf("\nElement at top of the stack: %d\n" ,peek());
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Element at top of the stack: 15
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
int peek(){
return stack[top];
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
return data;
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
printf("\nElement at top of the stack: %d\n" ,peek());
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Element at top of the stack: 15
public class Demo{
final static int MAXSIZE = 8;
public static int stack[] = new int[MAXSIZE];
public static int top = -1;
/* Check if the stack is full */
public static int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
public static int peek(){
return stack[top];
}
/* Function to insert into the stack */
public static int push(int data){
if(isfull() != 1) {
top = top + 1;
stack[top] = data;
} else {
System.out.print("Could not insert data, Stack is full.");
}
return data;
}
/* Main function */
public static void main(String[] args){
push(44);
push(10);
push(62);
push(123);
push(15);
System.out.print("Stack Elements: ");
// print stack data
for(int i = 0; i < MAXSIZE; i++) {
System.out.print(stack[i] + " ");
}
System.out.print("\nElement at top of the stack: " + peek());
}
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Element at top of the stack: 15
MAXSIZE = 8;
stack = [0] * MAXSIZE
top = -1
def isfull():
if(top == MAXSIZE):
return 1
else:
return 0
def peek():
return stack[top]
def push(data):
global top
if(isfull() != 1):
top = top + 1
stack[top] = data
else:
print("Could not insert data, Stack is full.")
return data
push(44);
push(10);
push(62);
push(123);
push(15);
print("Stack Elements: ")
for i in range(MAXSIZE):
print(stack[i], end = " ")
print("\nElement at top of the stack: ", peek())
Output
Stack Elements: 44 10 62 123 15 0 0 0 Element at top of the stack: 15
Verifying whether the Stack is full: isFull()
The isFull() operation checks whether the stack is full. This operation is used to check the status of the stack with the help of top pointer.
Algorithm
1. START 2. If the size of the stack is equal to the top position of the stack, the stack is full. Return 1. 3. Otherwise, return 0. 4. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Main function */
int main(){
printf("Stack full: %s\n" , isfull()?"true":"false");
return 0;
}
Output
Stack full: false
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Main function */
int main(){
printf("Stack full: %s\n" , isfull()?"true":"false");
return 0;
}
Output
Stack full: false
import java.io.*;
public class StackExample {
private int arr[];
private int top;
private int capacity;
StackExample(int size) {
arr = new int[size];
capacity = size;
top = -1;
}
public boolean isEmpty() {
return top == -1;
}
public boolean isFull() {
return top == capacity - 1;
}
public void push(int key) {
if (isFull()) {
System.out.println("Stack is Full\n");
return;
}
arr[++top] = key;
}
public static void main (String[] args) {
StackExample stk = new StackExample(5);
stk.push(1); // inserting 1 in the stack
stk.push(2);
stk.push(3);
stk.push(4);
stk.push(5);
System.out.println("Stack full: " + stk.isFull());
}
}
Output
Stack full: true
#python code for stack(IsFull)
MAXSIZE = 8
stack = [None] * MAXSIZE
top = -1
#Check if the stack is empty
def isfull():
if top == MAXSIZE - 1:
return True
else:
return False
#main function
print("Stack full:", isfull())
Output
Stack full: False
Verifying whether the Stack is empty: isEmpty()
The isEmpty() operation verifies whether the stack is empty. This operation is used to check the status of the stack with the help of top pointer.
Algorithm
1. START 2. If the top value is -1, the stack is empty. Return 1. 3. Otherwise, return 0. 4. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty() {
if(top == -1)
return 1;
else
return 0;
}
/* Main function */
int main() {
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
Output
Stack empty: true
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Main function */
int main(){
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
Output
Stack empty: true
public class Demo{
final static int MAXSIZE = 8;
static int stack[] = new int[MAXSIZE];
static int top = -1;
/* Check if the stack is empty */
public static int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Main function */
public static void main(String[] args){
boolean res = isempty() == 1 ? true : false;
System.out.print("Stack empty: " + res);
}
}
Output
Stack empty: true
#python code for stack(IsFull)
MAXSIZE = 8
stack = [None] * MAXSIZE
top = -1
#Check if the stack is empty
def isempty():
if top == -1:
return True
else:
return False
#main function
print("Stack empty:", isempty())
Output
Stack empty: True
Stack Complete implementation
Following are the complete implementations of Stack in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
int peek(){
return stack[top];
}
/* Function to delete from the stack */
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Element at top of the stack: %d\n" ,peek());
printf("Elements: \n");
// print stack data
while(!isempty()) {
int data = pop();
printf("%d\n",data);
}
printf("Stack full: %s\n" , isfull()?"true":"false");
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
Output
Element at top of the stack: 15 Elements: 15123 62 10 44 Stack full: false Stack empty: true
#include <iostream>
using namespace std;
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
int peek(){
return stack[top];
}
/* Function to delete from the stack */
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else
cout << "Could not retrieve data, Stack is empty." << endl;
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else
cout << "Could not insert data, Stack is full." << endl;
}
/* Main function */
int main(){
push(44);
push(10);
push(62);
push(123);
push(15);
cout << "Element at top of the stack: " << peek() << endl;
printf("Elements: \n");
// print stack data
while(!isempty()) {
int data = pop();
cout << data <<endl;
}
printf("Stack full: %s\n" , isfull()?"true":"false");
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
Output
Element at top of the stack: 15 Elements: 15 123 62 10 44 Stack full: false Stack empty: true
public class Demo{
final static int MAXSIZE = 8;
public static int stack[] = new int[MAXSIZE];
public static int top = -1;
/* Check if the stack is empty */
public static int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full */
public static int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
public static int peek(){
return stack[top];
}
/* Function to delete from the stack */
public static int pop(){
int data = 0;
if(isempty() != 1) {
data = stack[top];
top = top - 1;
return data;
} else
System.out.print("Could not retrieve data, Stack is empty.");
return data;
}
/* Function to insert into the stack */
public static int push(int data){
if(isfull() != 1) {
top = top + 1;
stack[top] = data;
} else
System.out.print("Could not insert data, Stack is full.");
return data;
}
/* Main function */
public static void main(String[] args){
push(44);
push(10);
push(62);
push(123);
push(15);
System.out.print("Element at top of the stack: " + peek());
System.out.print("\nElements: ");
// print stack data
while(isempty() != 1) {
int data = pop();
System.out.print(data + " ");
}
boolean res1 = isfull() == 1 ? true : false;
boolean res2 = isempty() == 1 ? true : false;
System.out.print("\nStack full: " + res1);
System.out.print("\nStack empty: " + res2);
}
}
Output
Element at top of the stack: 15 Elements: 15 123 62 10 44 Stack full: false Stack empty: true
MAXSIZE = 8
stack = [0] * MAXSIZE
top = -1;
def isempty():
if(top == -1):
return 1
else:
return 0
def isfull():
if(top == MAXSIZE):
return 1
else:
return 0
def peek():
return stack[top]
def pop():
global data, top
if(isempty() != 1):
data = stack[top];
top = top - 1;
return data
else:
print("Could not retrieve data, Stack is empty.")
return data
def push(data):
global top
if(isfull() != 1):
top = top + 1
stack[top] = data
else:
print("Could not insert data, Stack is full.")
return data
push(44)
push(10)
push(62)
push(123)
push(15)
print("Element at top of the stack: ", peek())
print("Elements: ")
while(isempty() != 1):
data = pop();
print(data, end = " ")
print("\nStack full: ",bool({True: 1, False: 0} [isfull() == 1]))
print("Stack empty: ",bool({True: 1, False: 0} [isempty() == 1]))
Output
Element at top of the stack: 15 Elements: 15 123 62 10 44 Stack full: False Stack empty: True
Stack Implementation in C
Click to check the implementation of Stack Program using C