Set Cover Problem

Table of content

The set cover algorithm provides solution to many real-world resource allocating problems. For instance, consider an airline assigning crew members to each of their airplanes such that they have enough people to fulfill the requirements for the journey. They take into account the flight timings, the duration, the pit-stops, availability of the crew to assign them to the flights. This is where set cover algorithm comes into picture.

Given a universal set U, containing few elements which are all divided into subsets. Considering the collection of these subsets as S = {S1, S2, S3, S4... Sn}, the set cover algorithm finds the minimum number of subsets such that they cover all the elements present in the universal set.

universal_set

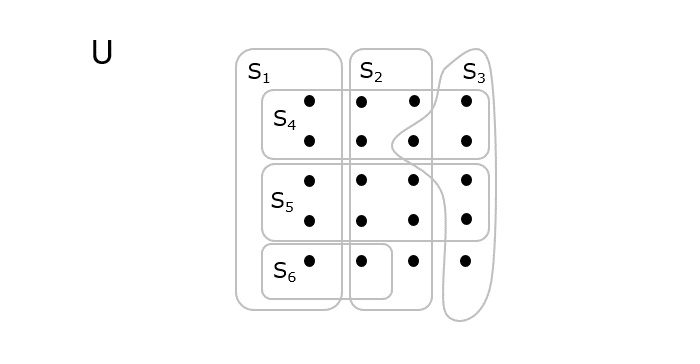
As shown in the above diagram, the dots represent the elements present in the universal set U that are divided into different sets, S = {S1, S2, S3, S4, S5, S6}. The minimum number of sets that need to be selected to cover all the elements will be the optimal output = {S1, S2, S3}.

Set Cover Algorithm

The set cover takes the collection of sets as an input and and returns the minimum number of sets required to include all the universal elements.

The set cover algorithm is an NP-Hard problem and a 2-approximation greedy algorithm.

Algorithm

Step 1 − Initialize Output = {} where Output represents the output set of elements.

Step 2 − While the Output set does not include all the elements in the universal set, do the following −

  • Find the cost-effectiveness of every subset present in the universal set using the formula, $\frac{Cost\left ( S_{i} \right )}{S_{i}-Output}$

  • Find the subset with minimum cost effectiveness for each iteration performed. Add the subset to the Output set.

Step 3 − Repeat Step 2 until there is no elements left in the universe. The output achieved is the final Output set.

Pseudocode

APPROX-GREEDY-SET_COVER(X, S)
   U = X
   OUTPUT = ф
   while U ≠ ф
      select Si Є S which has maximum |Si∩U|
   U = U – S
   OUTPUT = OUTPUT∪ {Si}
return OUTPUT

Analysis

assuming the overall number of elements equals the overall number of sets (|X| = |S|), the code runs in time O(|X|3)

Example

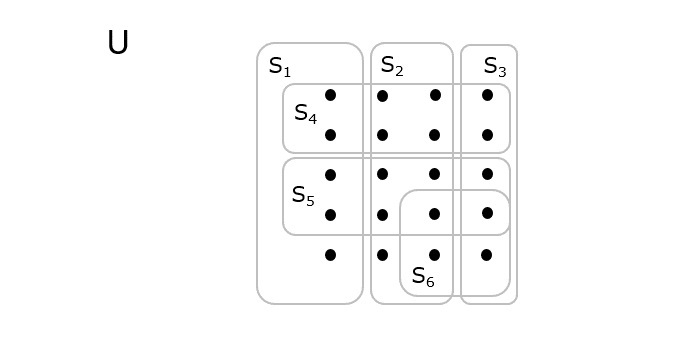
Set_Cover_Algorithm

Let us look at an example that describes the approximation algorithm for the set covering problem in more detail

S1 = {1, 2, 3, 4}                cost(S1) = 5
S2 = {2, 4, 5, 8, 10}            cost(S2) = 10
S3 = {1, 3, 5, 7, 9, 11, 13}     cost(S3) = 20
S4 = {4, 8, 12, 16, 20}          cost(S4) = 12
S5 = {5, 6, 7, 8, 9}             cost(S5) = 15

Step 1

The output set, Output = ф

Find the cost effectiveness of each set for no elements in the output set,

S1 = cost(S1) / (S1 – Output) = 5 / (4 – 0)
S2 = cost(S2) / (S2 – Output) = 10 / (5 – 0)
S3 = cost(S3) / (S3 – Output) = 20 / (7 – 0)
S4 = cost(S4) / (S4 – Output) = 12 / (5 – 0)
S5 = cost(S5) / (S5 – Output) = 15 / (5 – 0)

The minimum cost effectiveness in this iteration is achieved at S1, therefore, the subset added to the output set, Output = {S1} with elements {1, 2, 3, 4}

Step 2

Find the cost effectiveness of each set for the new elements in the output set,

S2 = cost(S2) / (S2 – Output) = 10 / (5 – 4)
S3 = cost(S3) / (S3 – Output) = 20 / (7 – 4)
S4 = cost(S4) / (S4 – Output) = 12 / (5 – 4)
S5 = cost(S5) / (S5 – Output) = 15 / (5 – 4)

The minimum cost effectiveness in this iteration is achieved at S3, therefore, the subset added to the output set, Output = {S1, S3} with elements {1, 2, 3, 4, 5, 7, 9, 11, 13}.

Step 3

Find the cost effectiveness of each set for the new elements in the output set,

S2 = cost(S2) / (S2 – Output) = 10 / |(5 – 9)|
S4 = cost(S4) / (S4 – Output) = 12 / |(5 – 9)|
S5 = cost(S5) / (S5 – Output) = 15 / |(5 – 9)|

The minimum cost effectiveness in this iteration is achieved at S2, therefore, the subset added to the output set, Output = {S1, S3, S2} with elements {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13}

Step 4

Find the cost effectiveness of each set for the new elements in the output set,

S4 = cost(S4) / (S4 – Output) = 12 / |(5 – 11)|
S5 = cost(S5) / (S5 – Output) = 15 / |(5 – 11)|

The minimum cost effectiveness in this iteration is achieved at S4, therefore, the subset added to the output set, Output = {S1, S3, S2, S4} with elements {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 13, 16, 20}

Step 5

Find the cost effectiveness of each set for the new elements in the output set,

S5 = cost(S5) / (S5 – Output) = 15 / |(5 – 14)|

The minimum cost effectiveness in this iteration is achieved at S5, therefore, the subset added to the output set, Output = {S1, S3, S2, S4, S5} with elements {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 16, 20}

The final output that covers all the elements present in the universal finite set is, Output = {S1, S3, S2, S4, S5}.

Implementation

Following are the implementations of the above approach in various programming langauges −

C C++ Java Python 
#include <stdio.h>
#define MAX_SETS 100
#define MAX_ELEMENTS 1000
int setCover(int X[], int S[][MAX_ELEMENTS], int numSets, int numElements, int output[]) {
   int U[MAX_ELEMENTS];
   for (int i = 0; i < numElements; i++) {
      U[i] = X[i];
   }
   int selectedSets[MAX_SETS];
   for (int i = 0; i < MAX_SETS; i++) {
      selectedSets[i] = 0; // Initialize all to 0 (not selected)
   }
   int outputIdx = 0;
   while (outputIdx < numSets) {  // Ensure we don't exceed the maximum number of sets
      int maxIntersectionSize = 0;
      int selectedSetIdx = -1;
      // Find the set Si with the maximum intersection with U
      for (int i = 0; i < numSets; i++) {
         if (selectedSets[i] == 0) { // Check if the set is not already selected
            int intersectionSize = 0;
            for (int j = 0; j < numElements; j++) {
               if (U[j] && S[i][j]) {
                  intersectionSize++;
               }
            }
            if (intersectionSize > maxIntersectionSize) {
               maxIntersectionSize = intersectionSize;
               selectedSetIdx = i;
            }
         }
      }
      // If no set found, break from the loop
      if (selectedSetIdx == -1) {
          break;
      }
      // Mark the selected set as "selected" in the array
      selectedSets[selectedSetIdx] = 1;
      // Remove the elements covered by the selected set from U
      for (int j = 0; j < numElements; j++) {
          U[j] = U[j] - S[selectedSetIdx][j];
      }
      // Add the selected set to the output
      output[outputIdx++] = selectedSetIdx;
   }
   return outputIdx;
}
int main() {
   int X[MAX_ELEMENTS] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
   int S[MAX_SETS][MAX_ELEMENTS] = {
      {1, 1, 0, 0, 0, 0, 0, 0, 0, 0},
      {0, 1, 1, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 1, 1, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 1, 1, 0, 0},
      {0, 0, 0, 0, 0, 0, 0, 1, 1, 1}
   };
   int numSets = 5;
   int numElements = 10;
   int output[MAX_SETS];
   int numSelectedSets = setCover(X, S, numSets, numElements, output);
   printf("Selected Sets: ");
   for (int i = 0; i < numSelectedSets; i++) {
      printf("%d ", output[i]);
   }
   printf("\n");
   return 0;
}

Output

Selected Sets: 1 2 3 4 0

#include <iostream>
#include <vector>
using namespace std;
#define MAX_SETS 100
#define MAX_ELEMENTS 1000
// Function to find the set cover using the Approximate Greedy Set Cover algorithm
int setCover(int X[], int S[][MAX_ELEMENTS], int numSets, int numElements, int output[])
{
   int U[MAX_ELEMENTS];
   for (int i = 0; i < numElements; i++) {
      U[i] = X[i];
   }
   int selectedSets[MAX_SETS];
   for (int i = 0; i < MAX_SETS; i++) {
      selectedSets[i] = 0; // Initialize all to 0 (not selected)
   }
   int outputIdx = 0;
   while (outputIdx < numSets) {  // Ensure we don't exceed the maximum number of sets
      int maxIntersectionSize = 0;
      int selectedSetIdx = -1;
      // Find the set Si with maximum intersection with U
      for (int i = 0; i < numSets; i++) {
         if (selectedSets[i] == 0) { // Check if the set is not already selected
            int intersectionSize = 0;
            for (int j = 0; j < numElements; j++) {
               if (U[j] && S[i][j]) {
                  intersectionSize++;
               }
            }
            if (intersectionSize > maxIntersectionSize) {
               maxIntersectionSize = intersectionSize;
               selectedSetIdx = i;
            }
         }
      }
      // If no set found, break from the loop
      if (selectedSetIdx == -1) {
         break;
      }
      // Mark the selected set as "selected" in the array
      selectedSets[selectedSetIdx] = 1;
      // Remove the elements covered by the selected set from U
      for (int j = 0; j < numElements; j++) {
         U[j] = U[j] - S[selectedSetIdx][j];
      }
      // Add the selected set to the output
      output[outputIdx++] = selectedSetIdx;
   }
   return outputIdx;
}
int main()
{
   int X[MAX_ELEMENTS] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
   int S[MAX_SETS][MAX_ELEMENTS] = {
      {1, 1, 0, 0, 0, 0, 0, 0, 0, 0},
      {0, 1, 1, 1, 0, 0, 0, 0, 0, 0},
      {0, 0, 0, 1, 1, 1, 0, 0, 0, 0},
      {0, 0, 0, 0, 0, 1, 1, 1, 0, 0},
      {0, 0, 0, 0, 0, 0, 0, 1, 1, 1}
   };
   int numSets = 5;
   int numElements = 10;
   int output[MAX_SETS];
   int numSelectedSets = setCover(X, S, numSets, numElements, output);
   cout << "Selected Sets: ";
   for (int i = 0; i < numSelectedSets; i++) {
       cout << output[i] << " ";
   }
   cout << endl;
   return 0;
}

Output

Selected Sets: 1 2 3 4 0 

import java.util.*;
public class SetCover {
   public static List<Integer> setCover(int[] X, int[][] S) {
      Set<Integer> U = new HashSet<>();
      for (int x : X) {
         U.add(x);
      }
      List<Integer> output = new ArrayList<>();
      while (!U.isEmpty()) {
         int maxIntersectionSize = 0;
         int selectedSetIdx = -1;
         for (int i = 0; i < S.length; i++) {
            int intersectionSize = 0;
            for (int j = 0; j < S[i].length; j++) {
               if (U.contains(S[i][j])) {
                  intersectionSize++;
               }
            }
            if (intersectionSize > maxIntersectionSize) {
               maxIntersectionSize = intersectionSize;
               selectedSetIdx = i;
            }
         }
         if (selectedSetIdx == -1) {
            break;
         }
         for (int j = 0; j < S[selectedSetIdx].length; j++) {
            U.remove(S[selectedSetIdx][j]);
         }
         output.add(selectedSetIdx);
      }
      return output;
   }
public static void main(String[] args) {
   int[] X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
   int[][] S = {
      {1, 2},
      {2, 3, 4},
      {4, 5, 6},
      {6, 7, 8},
      {8, 9, 10}
   };
   List<Integer> selectedSets = setCover(X, S);
   System.out.print("Selected Sets: ");
   for (int idx : selectedSets) {
      System.out.print(idx + " ");
   }
   System.out.println();
   }
}

Output

Selected Sets: 1 3 4 0 2 

def set_cover(X, S):
    U = set(X)
    output = []
    while U:
        max_intersection_size = 0
        selected_set_idx = -1
        for i, s in enumerate(S):
            intersection_size = len(U.intersection(s))
            if intersection_size > max_intersection_size:
                max_intersection_size = intersection_size
                selected_set_idx = i
        if selected_set_idx == -1:
            break
        U = U - set(S[selected_set_idx])
        output.append(selected_set_idx)
    return output
if __name__ == "__main__":
    X = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    S = [
        {1, 2},
        {2, 3, 4},
        {4, 5, 6},
        {6, 7, 8},
        {8, 9, 10}
    ]
    selected_sets = set_cover(X, S)
    print("Selected Sets:", selected_sets)

Output

Selected Sets: 1 3 4 0 2
Advertisements