
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Graph Data Structure
What is a Graph?
A graph is an abstract data type (ADT) which consists of a set of objects that are connected to each other via links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges.
Formally, a graph is a pair of sets (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph −
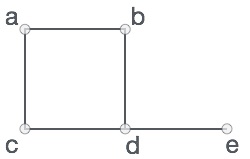
In the above graph,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
Graph Data Structure
Mathematical graphs can be represented in data structure. We can represent a graph using an array of vertices and a two-dimensional array of edges. Before we proceed further, let's familiarize ourselves with some important terms −
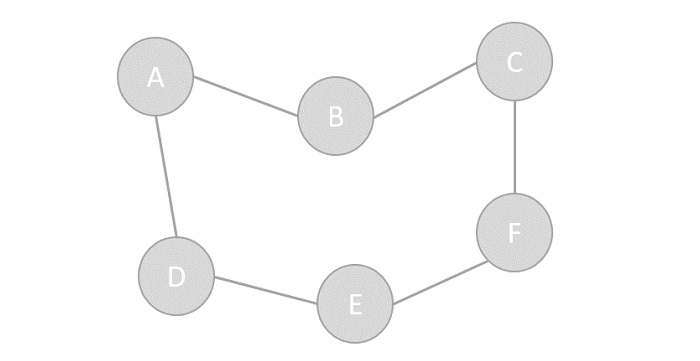
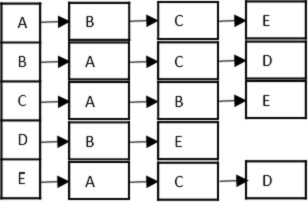
Vertex − Each node of the graph is represented as a vertex. In the following example, the labeled circle represents vertices. Thus, A to G are vertices. We can represent them using an array as shown in the following image. Here A can be identified by index 0. B can be identified using index 1 and so on.
Edge − Edge represents a path between two vertices or a line between two vertices. In the following example, the lines from A to B, B to C, and so on represents edges. We can use a two-dimensional array to represent an array as shown in the following image. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.
Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.

Operations of Graphs
The primary operations of a graph include creating a graph with vertices and edges, and displaying the said graph. However, one of the most common and popular operation performed using graphs are Traversal, i.e. visiting every vertex of the graph in a specific order.
There are two types of traversals in Graphs −
Depth First Search Traversal
Depth First Search is a traversal algorithm that visits all the vertices of a graph in the decreasing order of its depth. In this algorithm, an arbitrary node is chosen as the starting point and the graph is traversed back and forth by marking unvisited adjacent nodes until all the vertices are marked.
The DFS traversal uses the stack data structure to keep track of the unvisited nodes.
Click and check Depth First Search Traversal
Breadth First Search Traversal
Breadth First Search is a traversal algorithm that visits all the vertices of a graph present at one level of the depth before moving to the next level of depth. In this algorithm, an arbitrary node is chosen as the starting point and the graph is traversed by visiting the adjacent vertices on the same depth level and marking them until there is no vertex left.
The DFS traversal uses the queue data structure to keep track of the unvisited nodes.
Click and check Breadth First Search Traversal
Representation of Graphs
While representing graphs, we must carefully depict the elements (vertices and edges) present in the graph and the relationship between them. Pictorially, a graph is represented with a finite set of nodes and connecting links between them. However, we can also represent the graph in other most commonly used ways, like −
Adjacency Matrix
Adjacency List
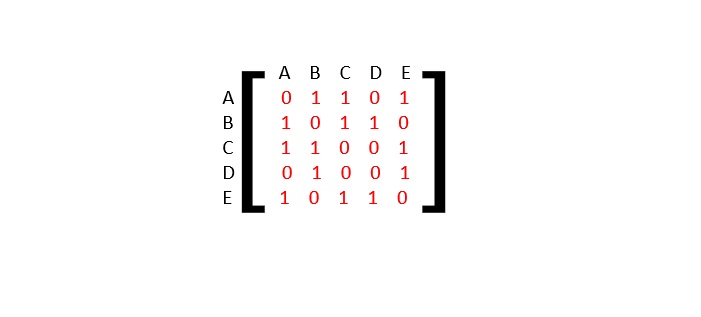
Adjacency Matrix
The Adjacency Matrix is a V x V matrix where the values are filled with either 0 or 1. If the link exists between Vi and Vj, it is recorded 1; otherwise, 0.
For the given graph below, let us construct an adjacency matrix −
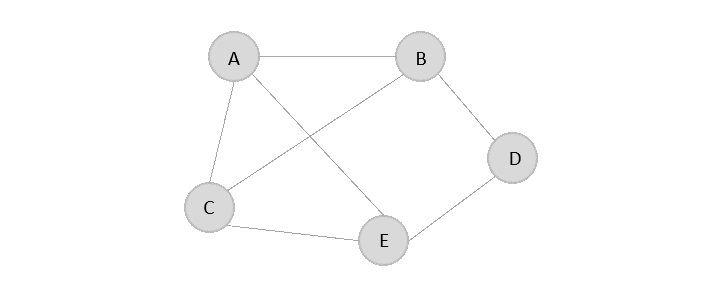
The adjacency matrix is −
Adjacency List
The adjacency list is a list of the vertices directly connected to the other vertices in the graph.

The adjacency list is −
Types of graph
There are two basic types of graph −
Directed Graph
Undirected Graph
Directed graph, as the name suggests, consists of edges that possess a direction that goes either away from a vertex or towards the vertex. Undirected graphs have edges that are not directed at all.
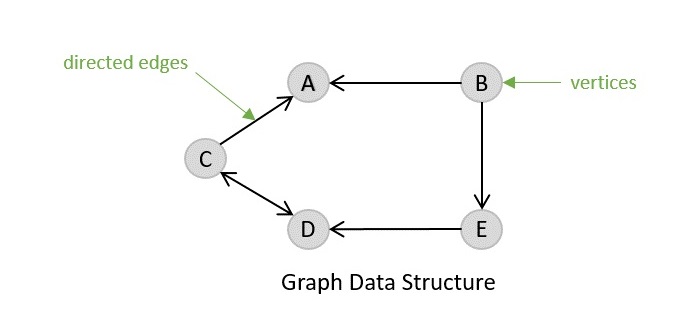
Directed Graph
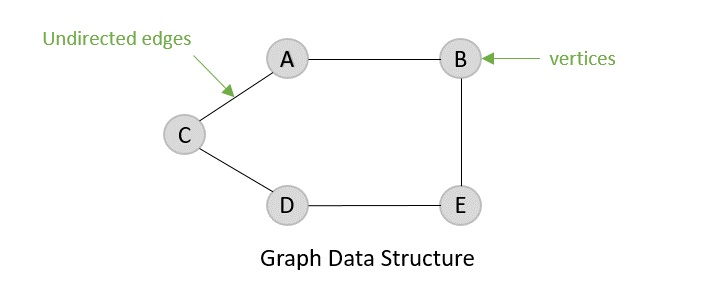
Undirected Graph
Spanning Tree
A spanning tree is a subset of an undirected graph that contains all the vertices of the graph connected with the minimum number of edges in the graph. Precisely, the edges of the spanning tree is a subset of the edges in the original graph.
If all the vertices are connected in a graph, then there exists at least one spanning tree. In a graph, there may exist more than one spanning tree.
Properties
A spanning tree does not have any cycle.
Any vertex can be reached from any other vertex.
Example
In the following graph, the highlighted edges form a spanning tree.
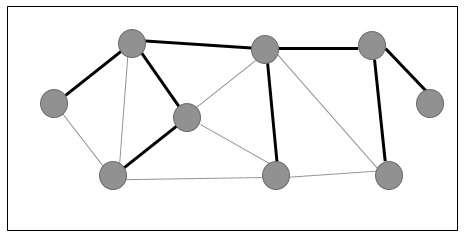
Minimum Spanning Tree
A Minimum Spanning Tree (MST) is a subset of edges of a connected weighted undirected graph that connects all the vertices together with the minimum possible total edge weight. To derive an MST, Prim's algorithm or Kruskal's algorithm can be used. Hence, we will discuss Prim's algorithm in this chapter.
As we have discussed, one graph may have more than one spanning tree. If there are n number of vertices, the spanning tree should have n − l1 number of edges. In this context, if each edge of the graph is associated with a weight and there exists more than one spanning tree, we need to find the minimum spanning tree of the graph.
Moreover, if there exist any duplicate weighted edges, the graph may have multiple minimum spanning tree.
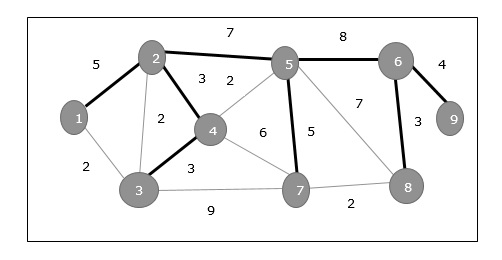
In the above graph, we have shown a spanning tree though it's not the minimum spanning tree. The cost of this spanning tree is (5+7+3+3+5+8+3+4)=38.
Shortest Path
The shortest path in a graph is defined as the minimum cost route from one vertex to another. This is most commonly seen in weighted directed graphs but are also applicable to undirected graphs.
A popular real−world application of finding the shortest path in a graph is a map. Navigation is made easier and simpler with the various shortest path algorithms where destinations are considered vertices of the graph and routes are the edges. The two common shortest path algorithms are −
Dijkstra's Shortest Path Algorithm
Bellman Ford's Shortest Path Algorithm
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
#include <stdlib.h>
#define V 5
// Maximum number of vertices in the graph
struct graph {
// declaring graph data structure
struct vertex *point[V];
};
struct vertex {
// declaring vertices
int end;
struct vertex *next;
};
struct Edge {
// declaring edges
int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
int i;
struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
for (i = 0; i < V; i++) {
graph->point[i] = NULL;
}
for (i = 0; i < x; i++) {
int start = edges[i].start;
int end = edges[i].end;
struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
v->end = end;
v->next = graph->point[start];
graph->point[start] = v;
}
return graph;
}
int main (){
struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
int n = sizeof (edges) / sizeof (edges[0]);
struct graph *graph = create_graph (edges, n);
printf("The graph created is: ");
for (int i = 0; i < V; i++) {
struct vertex *ptr = graph->point[i];
while (ptr != NULL) {
printf ("(%d -> %d)\t", i, ptr->end);
ptr = ptr->next;
}
printf ("\n");
}
return 0;
}
Output
The graph created is: (1 -> 3) (1 -> 0) (2 -> 1) (2 -> 0) (3 -> 2) (3 -> 0) (4 -> 2) (4 -> 1)
#include <bits/stdc++.h>
using namespace std;
#define V 5
// Maximum number of vertices in the graph
struct graph {
// declaring graph data structure
struct vertex *point[V];
};
struct vertex {
// declaring vertices
int end;
struct vertex *next;
};
struct Edge {
// declaring edges
int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
int i;
struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
for (i = 0; i < V; i++) {
graph->point[i] = NULL;
}
for (i = 0; i < x; i++) {
int start = edges[i].start;
int end = edges[i].end;
struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
v->end = end;
v->next = graph->point[start];
graph->point[start] = v;
}
return graph;
}
int main (){
struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
int n = sizeof (edges) / sizeof (edges[0]);
struct graph *graph = create_graph (edges, n);
int i;
cout<<"The graph created is: ";
for (i = 0; i < V; i++) {
struct vertex *ptr = graph->point[i];
while (ptr != NULL) {
cout << "(" << i << " -> " << ptr->end << ")\t";
ptr = ptr->next;
}
cout << endl;
}
return 0;
}
Output
The graph created is: (1 -> 3) (1 -> 0) (2 -> 1) (2 -> 0) (3 -> 2) (3 -> 0) (4 -> 2) (4 -> 1)
import java.util.*;
//class to store edges of the graph
class Edge {
int src, dest;
Edge(int src, int dest) {
this.src = src;
this.dest = dest;
}
}
// Graph class
public class Graph {
// node of adjacency list
static class vertex {
int v;
vertex(int v) {
this.v = v;
}
};
// define adjacency list to represent the graph
List<List<vertex>> adj_list = new ArrayList<>();
//Graph Constructor
public Graph(List<Edge> edges){
// adjacency list memory allocation
for (int i = 0; i < edges.size(); i++)
adj_list.add(i, new ArrayList<>());
// add edges to the graph
for (Edge e : edges){
// allocate new node in adjacency List from src to dest
adj_list.get(e.src).add(new vertex(e.dest));
}
}
public static void main (String[] args) {
// define edges of the graph
List<Edge> edges = Arrays.asList(new Edge(0, 1),new Edge(0, 2),
new Edge(0, 3),new Edge(1, 2), new Edge(1, 4),
new Edge(2, 4), new Edge(2, 3),new Edge(3, 1));
// call graph class Constructor to construct a graph
Graph graph = new Graph(edges);
// print the graph as an adjacency list
int src = 0;
int lsize = graph.adj_list.size();
System.out.println("The graph created is: ");
while (src < lsize) {
//traverse through the adjacency list and print the edges
for (vertex edge : graph.adj_list.get(src)) {
System.out.print(src + " -> " + edge.v + "\t");
}
System.out.println();
src++;
}
}
}
Output
The graph created is: 0 -> 1 0 -> 2 0 -> 3 1 -> 2 1 -> 4 2 -> 4 2 -> 3 3 -> 1
#Python code for Graph Data Struture
V = 5
#Maximum number of vertices in th graph
#Declaring vertices
class Vertex:
def __init__(self, end):
self.end = end
self.next = None
#Declaring Edges
class Edge:
def __init__(self, start, end):
self.start = start
self.end = end
#Declaring graph data structure
class Graph:
def __init__(self):
self.point = [None] * V
def create_graph(edges, x):
graph = Graph()
for i in range(V):
graph.point[i] = None
for i in range(x):
start = edges[i].start
end = edges[i].end
v = Vertex(end)
v.next = graph.point[start]
graph.point[start] = v
return graph
edges = [Edge(0, 1), Edge(0, 2), Edge(0, 3), Edge(1, 2), Edge(1, 4), Edge(2, 4), Edge(2, 3), Edge(3, 1)]
n = len(edges)
graph = create_graph(edges, n)
#Range
print("The graph created is: ")
for i in range(V):
ptr = graph.point[i]
while ptr is not None:
print("({} -> {})".format(i, ptr.end), end="\t")
ptr = ptr.next
print()
Output
The graph created is: (0 -> 3) (0 -> 2) (0 -> 1) (1 -> 4) (1 -> 2) (2 -> 3) (2 -> 4) (3 -> 1)