
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Shell Sort Algorithm
Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left.
This algorithm uses insertion sort on a widely spread elements, first to sort them and then sorts the less widely spaced elements. This spacing is termed as interval. This interval is calculated based on Knuth's formula as −
h = h * 3 + 1 where h is interval with initial value 1
This algorithm is quite efficient for medium-sized data sets as its average and worst case complexity are of O(n), where n is the number of items.
Shell Sort Algorithm
Following is the algorithm for shell sort.
1. Initialize the value of h. 2. Divide the list into smaller sub-list of equal interval h. 3. Sort these sub-lists using insertion sort. 4. Repeat until complete list is sorted.
Pseudocode
Following is the pseudocode for shell sort.
procedure shellSort()
A : array of items
/* calculate interval*/
while interval < A.length /3 do:
interval = interval * 3 + 1
end while
while interval > 0 do:
for outer = interval; outer < A.length; outer ++ do:
/* select value to be inserted */
valueToInsert = A[outer]
inner = outer;
/*shift element towards right*/
while inner > interval -1 && A[inner - interval]
>= valueToInsert do:
A[inner] = A[inner - interval]
inner = inner interval
end while
/* insert the number at hole position */
A[inner] = valueToInsert
end for
/* calculate interval*/
interval = (interval -1) /3;
end while
end procedure
Example
Let us consider the following example to have an idea of how shell sort works. We take the same array we have used in our previous examples. For our example and ease of understanding, we take the interval of 4. Make a virtual sub-list of all values located at the interval of 4 positions. Here these values are {35, 14}, {33, 19}, {42, 27} and {10, 14}

We compare values in each sub-list and swap them (if necessary) in the original array. After this step, the new array should look like this −
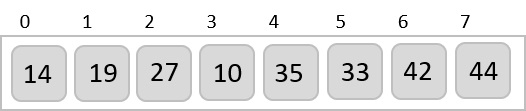
Then, we take interval of 2 and this gap generates two sub-lists - {14, 27, 35, 42}, {19, 10, 33, 44}
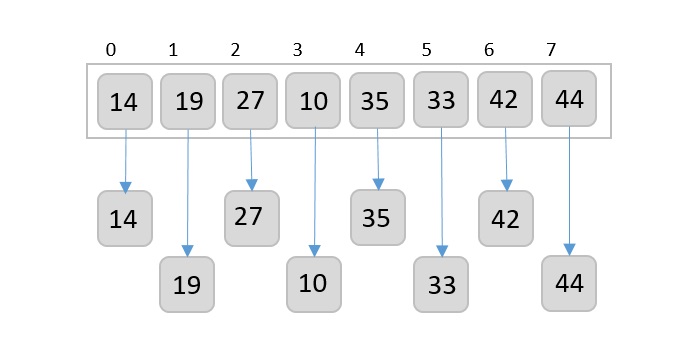
We compare and swap the values, if required, in the original array. After this step, the array should look like this −

Finally, we sort the rest of the array using interval of value 1. Shell sort uses insertion sort to sort the array.
Following is the step-by-step depiction −
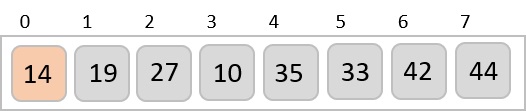
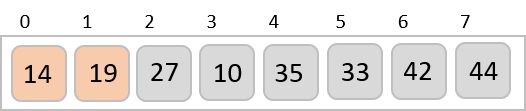
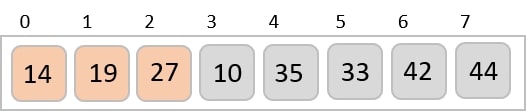
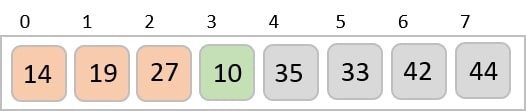
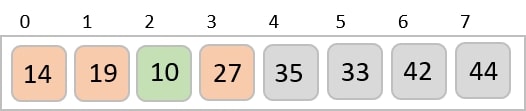
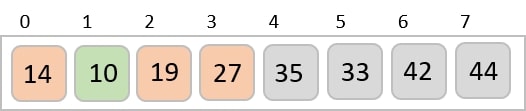
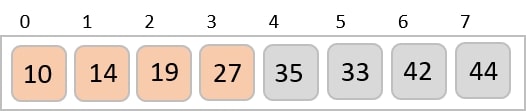
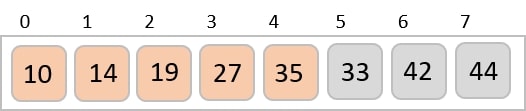
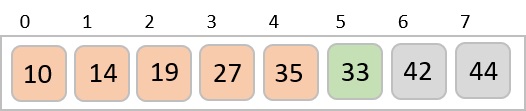
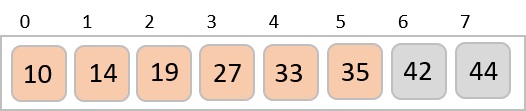
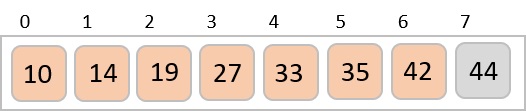
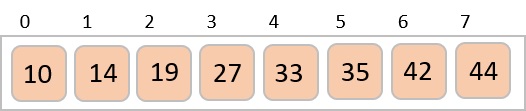
We see that it required only four swaps to sort the rest of the array.
Implementation
Shell sort is a highly efficient sorting algorithm and is based on insertion sort algorithm. This algorithm avoids large shifts as in case of insertion sort, if the smaller value is to the far right and has to be moved to the far left.
#include <stdio.h>
void shellSort(int arr[], int n){
int gap, j, k;
for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
for(j = gap; j<n; j++) {
for(k = j-gap; k>=0; k -= gap) {
if(arr[k+gap] >= arr[k])
break;
else {
int temp;
temp = arr[k+gap];
arr[k+gap] = arr[k];
arr[k] = temp;
}
}
}
}
}
int main(){
int n;
n = 5;
int arr[5] = {33, 45, 62, 12, 98}; // initialize the array
printf("Array before Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ",arr[i]);
printf("\n");
shellSort(arr, n);
printf("Array after Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ", arr[i]);
printf("\n");
}
Output
Array before Sorting: 33 45 62 12 98 Array after Sorting: 12 33 45 62 98
#include<iostream>
using namespace std;
void shellSort(int *arr, int n){
int gap, j, k;
for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
for(j = gap; j<n; j++) {
for(k = j-gap; k>=0; k -= gap) {
if(arr[k+gap] >= arr[k])
break;
else {
int temp;
temp = arr[k+gap];
arr[k+gap] = arr[k];
arr[k] = temp;
}
}
}
}
}
int main(){
int n;
n = 5;
int arr[5] = {33, 45, 62, 12, 98}; // initialize the array
cout << "Array before Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
shellSort(arr, n);
cout << "Array after Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
}
Output
Array before Sorting: 33 45 62 12 98 Array after Sorting: 12 33 45 62 98
import java.io.*;
import java.util.*;
public class ShellSort {
public static void main(String args[]) {
int n = 5;
int[] arr = {33, 45, 62, 12, 98}; //initialize an array
System.out.print("Array before Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
int gap;
for(gap = n/2; gap > 0; gap = gap / 2) { //initially gap = n/2, decreasing by gap /2
for(int j = gap; j<n; j++) {
for(int k = j-gap; k>=0; k -= gap) {
if(arr[k+gap] >= arr[k])
break;
else {
int temp;
temp = arr[k+gap];
arr[k+gap] = arr[k];
arr[k] = temp;
}
}
}
}
System.out.print("Array After Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}
Output
Array before Sorting: 33 45 62 12 98 Array After Sorting: 12 33 45 62 98
def shell_sort(array,n):
gap = n//2 #using floor division to avoid float values as result
while gap > 0:
for i in range(int(gap),n):
temp = array[i]
j = i
while j >= gap and array[j-gap] >temp:
array[j] = array[j-gap]
j -= gap
array[j] = temp
gap = gap // 2 #using floor division to avoid float values as result
arr = [33, 45, 62, 12, 98]
n = len(arr)
print("Array before Sorting: ")
print(arr)
shell_sort(arr, n);
print("Array after Sorting: ")
print(arr)
Output
Array before Sorting: [33, 45, 62, 12, 98] Array after Sorting: [12, 33, 45, 62, 98]
