
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Recursion Algorithms
Recursion
Some computer programming languages allow a module or function to call itself. This technique is known as recursion. In recursion, a function α either calls itself directly or calls a function β that in turn calls the original function α. The function α is called recursive function.
Example − a function calling itself.
int function(int value) {
if(value < 1)
return;
function(value - 1);
printf("%d ",value);
}
Example − a function that calls another function which in turn calls it again.
int function1(int value1) {
if(value1 < 1)
return;
function2(value1 - 1);
printf("%d ",value1);
}
int function2(int value2) {
function1(value2);
}
Properties
A recursive function can go infinite like a loop. To avoid infinite running of recursive function, there are two properties that a recursive function must have −
Base criteria − There must be at least one base criteria or condition, such that, when this condition is met the function stops calling itself recursively.
Progressive approach − The recursive calls should progress in such a way that each time a recursive call is made it comes closer to the base criteria.
Implementation
Many programming languages implement recursion by means of stacks. Generally, whenever a function (caller) calls another function (callee) or itself as callee, the caller function transfers execution control to the callee. This transfer process may also involve some data to be passed from the caller to the callee.
This implies, the caller function has to suspend its execution temporarily and resume later when the execution control returns from the callee function. Here, the caller function needs to start exactly from the point of execution where it puts itself on hold. It also needs the exact same data values it was working on. For this purpose, an activation record (or stack frame) is created for the caller function.
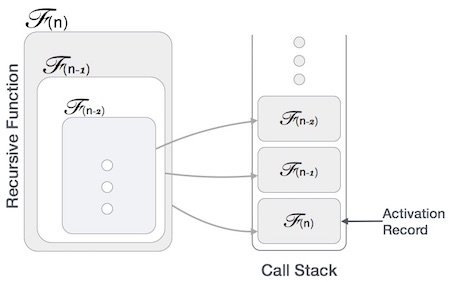
This activation record keeps the information about local variables, formal parameters, return address and all information passed to the caller function.
Analysis of Recursion
One may argue why to use recursion, as the same task can be done with iteration. The first reason is, recursion makes a program more readable and because of latest enhanced CPU systems, recursion is more efficient than iterations.
Time Complexity
In case of iterations, we take number of iterations to count the time complexity. Likewise, in case of recursion, assuming everything is constant, we try to figure out the number of times a recursive call is being made. A call made to a function is Ο(1), hence the (n) number of times a recursive call is made makes the recursive function Ο(n).
Space Complexity
Space complexity is counted as what amount of extra space is required for a module to execute. In case of iterations, the compiler hardly requires any extra space. The compiler keeps updating the values of variables used in the iterations. But in case of recursion, the system needs to store activation record each time a recursive call is made. Hence, it is considered that space complexity of recursive function may go higher than that of a function with iteration.
Example
Following are the implementations of the recursion in various programming languages −
// C program for Recursion Data Structure
#include <stdio.h>
int factorial(int n) {
// Base case: factorial of 0 is 1
if (n == 0)
return 1;
// Recursive case: multiply n with factorial of (n-1)
return n * factorial(n - 1);
}
int main() {
// case 1
int number = 6;
printf("Number is: %d\n" , 6);
//case 2
if (number < 0) {
printf("Error: Factorial is undefined for negative numbers.\n");
return 1;
}
int result = factorial(number);
//print the output
printf("Factorial of %d is: %d\n", number, result);
return 0;
}
Output
Number is: 6 Factorial of 6 is: 720
// CPP program for Recursion Data Structure
#include <iostream>
int factorial(int n) {
// Base case: factorial of 0 is 1
if (n == 0)
return 1;
// Recursive case: multiply n with factorial of (n-1)
return n * factorial(n - 1);
}
int main() {
// case 1
int number = 6;
std::cout<<"Number is: "<<number<<"\n";
//case 2
if (number < 0) {
std::cout << "Error: Factorial is undefined for negative numbers.\n";
return 1;
}
int result = factorial(number);
//print the output
std::cout << "Factorial of " << number << " is: " << result << std::endl;
return 0;
}
Output
Number is: 6 Factorial of 6 is: 720
// Java program for Recursion Data Structure
import java.util.Scanner;
public class Main {
public static int factorial(int n) {
// Base case: factorial of 0 is 1
if (n == 0)
return 1;
// Recursive case: multiply n with factorial of (n-1)
return n * factorial(n - 1);
}
public static void main(String[] args) {
//Case 1
int number = 6;
System.out.println("Number is: " + number);
//Case 2
if (number < 0) {
System.out.println("Error: Factorial is undefined for negative numbers.");
System.exit(1);
}
int result = factorial(number);
//print the output
System.out.println("Factorial of " + number + " is: " + result);
}
}
Output
Number is: 6 Factorial of 6 is: 720
# Python program for Recursion Data Structure
def factorial(n):
#Base Case: factorial of 0 is 1
if n == 0:
return 1
# Recursive case: multiply n with factorial of (n-1)
return n * factorial(n - 1)
#Case 1:
number = 6;
print("Number is: ", number);
#Case 2:
if number < 0:
print("Error: Factorial is undefined for negative numbers.")
else:
result = factorial(number)
# print the output
print("Factorial of", number, "is: ", result)
Output
Number is: 6 Factorial of 6 is: 720
