
- DSA - Home
- DSA - Overview
- DSA - Environment Setup
- DSA - Algorithms Basics
- DSA - Asymptotic Analysis
- Data Structures
- DSA - Data Structure Basics
- DSA - Data Structures and Types
- DSA - Array Data Structure
- DSA - Skip List Data Structure
- Linked Lists
- DSA - Linked List Data Structure
- DSA - Doubly Linked List Data Structure
- DSA - Circular Linked List Data Structure
- Stack & Queue
- DSA - Stack Data Structure
- DSA - Expression Parsing
- DSA - Queue Data Structure
- DSA - Circular Queue Data Structure
- DSA - Priority Queue Data Structure
- DSA - Deque Data Structure
- Searching Algorithms
- DSA - Searching Algorithms
- DSA - Linear Search Algorithm
- DSA - Binary Search Algorithm
- DSA - Interpolation Search
- DSA - Jump Search Algorithm
- DSA - Exponential Search
- DSA - Fibonacci Search
- DSA - Sublist Search
- DSA - Hash Table
- Sorting Algorithms
- DSA - Sorting Algorithms
- DSA - Bubble Sort Algorithm
- DSA - Insertion Sort Algorithm
- DSA - Selection Sort Algorithm
- DSA - Merge Sort Algorithm
- DSA - Shell Sort Algorithm
- DSA - Heap Sort Algorithm
- DSA - Bucket Sort Algorithm
- DSA - Counting Sort Algorithm
- DSA - Radix Sort Algorithm
- DSA - Quick Sort Algorithm
- Matrices Data Structure
- DSA - Matrices Data Structure
- DSA - Lup Decomposition In Matrices
- DSA - Lu Decomposition In Matrices
- Graph Data Structure
- DSA - Graph Data Structure
- DSA - Depth First Traversal
- DSA - Breadth First Traversal
- DSA - Spanning Tree
- DSA - Topological Sorting
- DSA - Strongly Connected Components
- DSA - Biconnected Components
- DSA - Augmenting Path
- DSA - Network Flow Problems
- DSA - Flow Networks In Data Structures
- DSA - Edmonds Blossom Algorithm
- DSA - Maxflow Mincut Theorem
- Tree Data Structure
- DSA - Tree Data Structure
- DSA - Tree Traversal
- DSA - Binary Search Tree
- DSA - AVL Tree
- DSA - Red Black Trees
- DSA - B Trees
- DSA - B+ Trees
- DSA - Splay Trees
- DSA - Range Queries
- DSA - Segment Trees
- DSA - Fenwick Tree
- DSA - Fusion Tree
- DSA - Hashed Array Tree
- DSA - K-Ary Tree
- DSA - Kd Trees
- DSA - Priority Search Tree Data Structure
- Recursion
- DSA - Recursion Algorithms
- DSA - Tower of Hanoi Using Recursion
- DSA - Fibonacci Series Using Recursion
- Divide and Conquer
- DSA - Divide and Conquer
- DSA - Max-Min Problem
- DSA - Strassen's Matrix Multiplication
- DSA - Karatsuba Algorithm
- Greedy Algorithms
- DSA - Greedy Algorithms
- DSA - Travelling Salesman Problem (Greedy Approach)
- DSA - Prim's Minimal Spanning Tree
- DSA - Kruskal's Minimal Spanning Tree
- DSA - Dijkstra's Shortest Path Algorithm
- DSA - Map Colouring Algorithm
- DSA - Fractional Knapsack Problem
- DSA - Job Sequencing with Deadline
- DSA - Optimal Merge Pattern Algorithm
- Dynamic Programming
- DSA - Dynamic Programming
- DSA - Matrix Chain Multiplication
- DSA - Floyd Warshall Algorithm
- DSA - 0-1 Knapsack Problem
- DSA - Longest Common Sub-sequence Algorithm
- DSA - Travelling Salesman Problem (Dynamic Approach)
- Hashing
- DSA - Hashing Data Structure
- DSA - Collision In Hashing
- Disjoint Set
- DSA - Disjoint Set
- DSA - Path Compression And Union By Rank
- Heap
- DSA - Heap Data Structure
- DSA - Binary Heap
- DSA - Binomial Heap
- DSA - Fibonacci Heap
- Tries Data Structure
- DSA - Tries
- DSA - Standard Tries
- DSA - Compressed Tries
- DSA - Suffix Tries
- Treaps
- DSA - Treaps Data Structure
- Bit Mask
- DSA - Bit Mask In Data Structures
- Bloom Filter
- DSA - Bloom Filter Data Structure
- Approximation Algorithms
- DSA - Approximation Algorithms
- DSA - Vertex Cover Algorithm
- DSA - Set Cover Problem
- DSA - Travelling Salesman Problem (Approximation Approach)
- Randomized Algorithms
- DSA - Randomized Algorithms
- DSA - Randomized Quick Sort Algorithm
- DSA - Karger’s Minimum Cut Algorithm
- DSA - Fisher-Yates Shuffle Algorithm
- Miscellaneous
- DSA - Infix to Postfix
- DSA - Bellmon Ford Shortest Path
- DSA - Maximum Bipartite Matching
- DSA Useful Resources
- DSA - Questions and Answers
- DSA - Selection Sort Interview Questions
- DSA - Merge Sort Interview Questions
- DSA - Insertion Sort Interview Questions
- DSA - Heap Sort Interview Questions
- DSA - Bubble Sort Interview Questions
- DSA - Bucket Sort Interview Questions
- DSA - Radix Sort Interview Questions
- DSA - Cycle Sort Interview Questions
- DSA - Quick Guide
- DSA - Useful Resources
- DSA - Discussion
Data Structures & Algorithms - Quick Guide
Overview
Data Structure is a systematic way to organize data in order to use it efficiently. Following terms are the foundation terms of a data structure.
Interface − Each data structure has an interface. Interface represents the set of operations that a data structure supports. An interface only provides the list of supported operations, type of parameters they can accept and return type of these operations.
Implementation − Implementation provides the internal representation of a data structure. Implementation also provides the definition of the algorithms used in the operations of the data structure.
Characteristics of a Data Structure
Correctness − Data structure implementation should implement its interface correctly.
Time Complexity − Running time or the execution time of operations of data structure must be as small as possible.
Space Complexity − Memory usage of a data structure operation should be as little as possible.
Need for Data Structure
As applications are getting complex and data rich, there are three common problems that applications face now-a-days.
Data Search − Consider an inventory of 1 million(106) items of a store. If the application is to search an item, it has to search an item in 1 million(106) items every time slowing down the search. As data grows, search will become slower.
Processor speed − Processor speed although being very high, falls limited if the data grows to billion records.
Multiple requests − As thousands of users can search data simultaneously on a web server, even the fast server fails while searching the data.
To solve the above-mentioned problems, data structures come to rescue. Data can be organized in a data structure in such a way that all items may not be required to be searched, and the required data can be searched almost instantly.
Execution Time Cases
There are three cases which are usually used to compare various data structure's execution time in a relative manner.
Worst Case − This is the scenario where a particular data structure operation takes maximum time it can take. If an operation's worst case time is ƒ(n) then this operation will not take more than ƒ(n) time where ƒ(n) represents function of n.
Average Case − This is the scenario depicting the average execution time of an operation of a data structure. If an operation takes ƒ(n) time in execution, then m operations will take mƒ(n) time.
Best Case − This is the scenario depicting the least possible execution time of an operation of a data structure. If an operation takes ƒ(n) time in execution, then the actual operation may take time as the random number which would be maximum as ƒ(n).
Basic Terminology
Data − Data are values or set of values.
Data Item − Data item refers to single unit of values.
Group Items − Data items that are divided into sub items are called as Group Items.
Elementary Items − Data items that cannot be divided are called as Elementary Items.
Attribute and Entity − An entity is that which contains certain attributes or properties, which may be assigned values.
Entity Set − Entities of similar attributes form an entity set.
Field − Field is a single elementary unit of information representing an attribute of an entity.
Record − Record is a collection of field values of a given entity.
File − File is a collection of records of the entities in a given entity set.
Environment Setup
Local Environment Setup
If you are still willing to set up your environment for C programming language, you need the following two tools available on your computer, (a) Text Editor and (b) The C Compiler.
Text Editor
This will be used to type your program. Examples of few editors include Windows Notepad, OS Edit command, Brief, Epsilon, EMACS, and vim or vi.
The name and the version of the text editor can vary on different operating systems. For example, Notepad will be used on Windows, and vim or vi can be used on Windows as well as Linux or UNIX.
The files you create with your editor are called source files and contain program source code. The source files for C programs are typically named with the extension ".c".
Before starting your programming, make sure you have one text editor in place and you have enough experience to write a computer program, save it in a file, compile it, and finally execute it.
The C Compiler
The source code written in the source file is the human readable source for your program. It needs to be "compiled", to turn into machine language so that your CPU can actually execute the program as per the given instructions.
This C programming language compiler will be used to compile your source code into a final executable program. We assume you have the basic knowledge about a programming language compiler.
Most frequently used and free available compiler is GNU C/C++ compiler. Otherwise, you can have compilers either from HP or Solaris if you have respective Operating Systems (OS).
The following section guides you on how to install GNU C/C++ compiler on various OS. We are mentioning C/C++ together because GNU GCC compiler works for both C and C++ programming languages.
Installation on UNIX/Linux
If you are using Linux or UNIX, then check whether GCC is installed on your system by entering the following command from the command line −
$ gcc -v
If you have GNU compiler installed on your machine, then it should print a message such as the following −
Using built-in specs. Target: i386-redhat-linux Configured with: ../configure --prefix = /usr ....... Thread model: posix gcc version 4.1.2 20080704 (Red Hat 4.1.2-46)
If GCC is not installed, then you will have to install it yourself using the detailed instructions available at https://gcc.gnu.org/install/
This tutorial has been written based on Linux and all the given examples have been compiled on Cent OS flavor of Linux system.
Installation on Mac OS
If you use Mac OS X, the easiest way to obtain GCC is to download the Xcode development environment from Apple's website and follow the simple installation instructions. Once you have Xcode setup, you will be able to use GNU compiler for C/C++.
Xcode is currently available at developer.apple.com/technologies/tools/
Installation on Windows
To install GCC on Windows, you need to install MinGW. To install MinGW, go to the MinGW homepage, www.mingw.org, and follow the link to the MinGW download page. Download the latest version of the MinGW installation program, which should be named MinGW-<version>.exe.
While installing MinWG, at a minimum, you must install gcc-core, gcc-g++, binutils, and the MinGW runtime, but you may wish to install more.
Add the bin subdirectory of your MinGW installation to your PATH environment variable, so that you can specify these tools on the command line by their simple names.
When the installation is complete, you will be able to run gcc, g++, ar, ranlib, dlltool, and several other GNU tools from the Windows command line.
Data Structure Basics
This chapter explains the basic terms related to data structure.
Data Definition
Data Definition defines a particular data with the following characteristics.
Atomic − Definition should define a single concept.
Traceable − Definition should be able to be mapped to some data element.
Accurate − Definition should be unambiguous.
Clear and Concise − Definition should be understandable.
Data Object
Data Object represents an object having a data.
Data Type
Data type is a way to classify various types of data such as integer, string, etc. which determines the values that can be used with the corresponding type of data, the type of operations that can be performed on the corresponding type of data. There are two data types −
- Built-in Data Type
- Derived Data Type
Built-in Data Type
Those data types for which a language has built-in support are known as Built-in Data types. For example, most of the languages provide the following built-in data types.
- Integers
- Boolean (true, false)
- Floating (Decimal numbers)
- Character and Strings
Derived Data Type
Those data types which are implementation independent as they can be implemented in one or the other way are known as derived data types. These data types are normally built by the combination of primary or built-in data types and associated operations on them. For example −
- List
- Array
- Stack
- Queue
Basic Operations
The data in the data structures are processed by certain operations. The particular data structure chosen largely depends on the frequency of the operation that needs to be performed on the data structure.
- Traversing
- Searching
- Insertion
- Deletion
- Sorting
- Merging
Data Structures and Types
Data structures are introduced in order to store, organize and manipulate data in programming languages. They are designed in a way that makes accessing and processing of the data a little easier and simpler. These data structures are not confined to one particular programming language; they are just pieces of code that structure data in the memory.
Data types are often confused as a type of data structures, but it is not precisely correct even though they are referred to as Abstract Data Types. Data types represent the nature of the data while data structures are just a collection of similar or different data types in one.
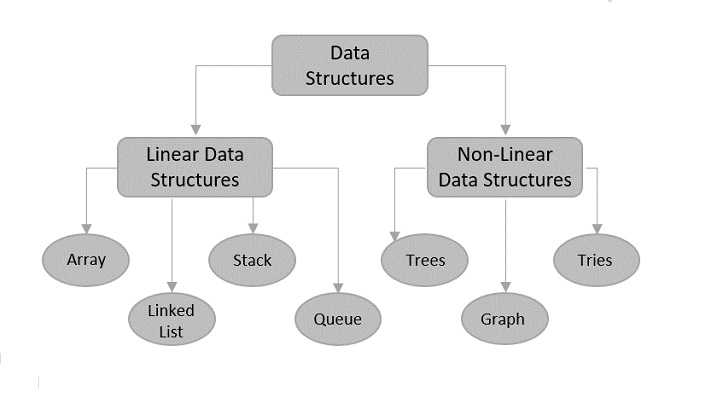
There are usually just two types of data structures −
Linear
Non-Linear
Linear Data Structures
The data is stored in linear data structures sequentially. These are rudimentary structures since the elements are stored one after the other without applying any mathematical operations.

Linear data structures are usually easy to implement but since the memory allocation might become complicated, time and space complexities increase. Few examples of linear data structures include −
Arrays
Linked Lists
Stacks
Queues
Based on the data storage methods, these linear data structures are divided into two sub-types. They are − static and dynamic data structures.
Static Linear Data Structures
In Static Linear Data Structures, the memory allocation is not scalable. Once the entire memory is used, no more space can be retrieved to store more data. Hence, the memory is required to be reserved based on the size of the program. This will also act as a drawback since reserving more memory than required can cause a wastage of memory blocks.
The best example for static linear data structures is an array.
Dynamic Linear Data Structures
In Dynamic linear data structures, the memory allocation can be done dynamically when required. These data structures are efficient considering the space complexity of the program.
Few examples of dynamic linear data structures include: linked lists, stacks and queues.
Non-Linear Data Structures
Non-Linear data structures store the data in the form of a hierarchy. Therefore, in contrast to the linear data structures, the data can be found in multiple levels and are difficult to traverse through.
However, they are designed to overcome the issues and limitations of linear data structures. For instance, the main disadvantage of linear data structures is the memory allocation. Since the data is allocated sequentially in linear data structures, each element in these data structures uses one whole memory block. However, if the data uses less memory than the assigned block can hold, the extra memory space in the block is wasted. Therefore, non-linear data structures are introduced. They decrease the space complexity and use the memory optimally.
Few types of non-linear data structures are −
Graphs
Trees
Tries
Maps
Array Data Structure
Array is a type of linear data structure that is defined as a collection of elements with same or different data types. They exist in both single dimension and multiple dimensions. These data structures come into picture when there is a necessity to store multiple elements of similar nature together at one place.
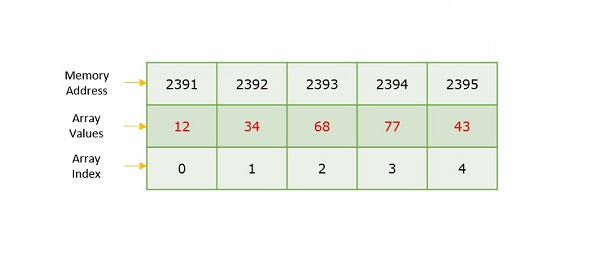
The difference between an array index and a memory address is that the array index acts like a key value to label the elements in the array. However, a memory address is the starting address of free memory available.
Following are the important terms to understand the concept of Array.
Element − Each item stored in an array is called an element.
Index − Each location of an element in an array has a numerical index, which is used to identify the element.
Syntax
Creating an array in C and C++ programming languages −
data_type array_name[array_size] = {elements separated using commas}
or,
data_type array_name[array_size];
Creating an array in Java programming language −
data_type[] array_name = {elements separated by commas}
or,
data_type array_name = new data_type[array_size];
Need for Arrays
Arrays are used as solutions to many problems from the small sorting problems to more complex problems like travelling salesperson problem. There are many data structures other than arrays that provide efficient time and space complexity for these problems, so what makes using arrays better? The answer lies in the random access lookup time.
Arrays provide O(1) random access lookup time. That means, accessing the 1st index of the array and the 1000th index of the array will both take the same time. This is due to the fact that array comes with a pointer and an offset value. The pointer points to the right location of the memory and the offset value shows how far to look in the said memory.
array_name[index]
| |
Pointer Offset
Therefore, in an array with 6 elements, to access the 1st element, array is pointed towards the 0th index. Similarly, to access the 6th element, array is pointed towards the 5th index.
Array Representation
Arrays are represented as a collection of buckets where each bucket stores one element. These buckets are indexed from 0 to n-1, where n is the size of that particular array. For example, an array with size 10 will have buckets indexed from 0 to 9.
This indexing will be similar for the multidimensional arrays as well. If it is a 2-dimensional array, it will have sub-buckets in each bucket. Then it will be indexed as array_name[m][n], where m and n are the sizes of each level in the array.
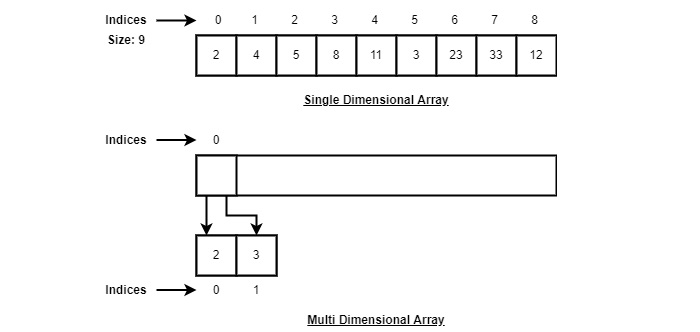
As per the above illustration, following are the important points to be considered.
Index starts with 0.
Array length is 9 which means it can store 9 elements.
Each element can be accessed via its index. For example, we can fetch an element at index 6 as 23.
Basic Operations in the Arrays
The basic operations in the Arrays are insertion, deletion, searching, display, traverse, and update. These operations are usually performed to either modify the data in the array or to report the status of the array.
Following are the basic operations supported by an array.
Traverse − print all the array elements one by one.
Insertion − Adds an element at the given index.
Deletion − Deletes an element at the given index.
Search − Searches an element using the given index or by the value.
Update − Updates an element at the given index.
Display − Displays the contents of the array.
In C, when an array is initialized with size, then it assigns defaults values to its elements in following order.
| Data Type | Default Value |
|---|---|
| bool | false |
| char | 0 |
| int | 0 |
| float | 0.0 |
| double | 0.0f |
| void | |
| wchar_t | 0 |
Insertion Operation
In the insertion operation, we are adding one or more elements to the array. Based on the requirement, a new element can be added at the beginning, end, or any given index of array. This is done using input statements of the programming languages.
Algorithm
Following is an algorithm to insert elements into a Linear Array until we reach the end of the array −
1. Start 2. Create an Array of a desired datatype and size. 3. Initialize a variable i as 0. 4. Enter the element at ith index of the array. 5. Increment i by 1. 6. Repeat Steps 4 & 5 until the end of the array. 7. Stop
Here, we see a practical implementation of insertion operation, where we add data at the end of the array −
Example
#include <stdio.h>
int main(){
int LA[3] = {}, i;
printf("Array Before Insertion:\n");
for(i = 0; i < 3; i++)
printf("LA[%d] = %d \n", i, LA[i]);
printf("Inserting Elements.. \n");
printf("The array elements after insertion :\n"); // prints array values
for(i = 0; i < 3; i++) {
LA[i] = i + 2;
printf("LA[%d] = %d \n", i, LA[i]);
}
return 0;
}
Output
Array Before Insertion: LA[0] = 0 LA[1] = 0 LA[2] = 0 Inserting Elements.. The array elements after insertion : LA[0] = 2 LA[1] = 3 LA[2] = 4
#include <iostream>
using namespace std;
int main(){
int LA[3] = {}, i;
cout << "Array Before Insertion:" << endl;
for(i = 0; i < 3; i++)
cout << "LA[" << i <<"] = " << LA[i] << endl;
//prints garbage values
cout << "Inserting elements.." <<endl;
cout << "Array After Insertion:" << endl; // prints array values
for(i = 0; i < 5; i++) {
LA[i] = i + 2;
cout << "LA[" << i <<"] = " << LA[i] << endl;
}
return 0;
}
Output
Array Before Insertion: LA[0] = 0 LA[1] = 0 LA[2] = 0 Inserting elements.. Array After Insertion: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 5 LA[4] = 6
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[3];
System.out.println("Array Before Insertion:");
for(int i = 0; i < 3; i++)
System.out.println("LA[" + i + "] = " + LA[i]); //prints empty array
System.out.println("Inserting Elements..");
// Printing Array after Insertion
System.out.println("Array After Insertion:");
for(int i = 0; i < 3; i++) {
LA[i] = i+3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
Output
Array Before Insertion: LA[0] = 0 LA[1] = 0 LA[2] = 0 Inserting Elements.. Array After Insertion: LA[0] = 3 LA[1] = 4 LA[2] = 5
# python program to insert element using insert operation
def insert(arr, element):
arr.append(element)
# Driver's code
if __name__ == '__main__':
# declaring array and value to insert
LA = [0, 0, 0]
x = 0
# array before inserting an element
print("Array Before Insertion: ")
for x in range(len(LA)):
print("LA", [x], " = " , LA[x])
print("Inserting elements....")
# array after Inserting element
for x in range(len(LA)):
LA.append(x);
LA[x] = x+1;
print("Array After Insertion: ")
for x in range(len(LA)):
print("LA", [x], " = " , LA[x])
Output
Array Before Insertion: LA [0] = 0 LA [1] = 0 LA [2] = 0 Inserting elements.... Array After Insertion: LA [0] = 1 LA [1] = 2 LA [2] = 3 LA [3] = 0 LA [4] = 1 LA [5] = 2
For other variations of array insertion operation, click here.
Deletion Operation
In this array operation, we delete an element from the particular index of an array. This deletion operation takes place as we assign the value in the consequent index to the current index.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to delete an element available at the Kth position of LA.
1. Start 2. Set J = K 3. Repeat steps 4 and 5 while J < N 4. Set LA[J] = LA[J + 1] 5. Set J = J+1 6. Set N = N-1 7. Stop
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
void main(){
int LA[] = {1,3,5};
int n = 3;
int i;
printf("The original array elements are :\n");
for(i = 0; i<n; i++)
printf("LA[%d] = %d \n", i, LA[i]);
for(i = 1; i<n; i++) {
LA[i] = LA[i+1];
n = n - 1;
}
printf("The array elements after deletion :\n");
for(i = 0; i<n; i++)
printf("LA[%d] = %d \n", i, LA[i]);
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 The array elements after deletion : LA[0] = 1 LA[1] = 5
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5};
int i, n = 3;
cout << "The original array elements are :"<<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] << endl;
}
for(i = 1; i<n; i++) {
LA[i] = LA[i+1];
n = n - 1;
}
cout << "The array elements after deletion :"<<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] <<endl;
}
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 The array elements after deletion : LA[0] = 1 LA[1] = 5
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[3];
int n = LA.length;
System.out.println("Array Before Deletion:");
for(int i = 0; i < n; i++) {
LA[i] = i + 3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
for(int i = 1; i<n-1; i++) {
LA[i] = LA[i+1];
n = n - 1;
}
System.out.println("Array After Deletion:");
for(int i = 0; i < n; i++) {
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
Output
Array Before Deletion: LA[0] = 3 LA[1] = 4 LA[2] = 5 Array After Deletion: LA[0] = 3 LA[1] = 5
#python program to delete the value using delete operation
if __name__ == '__main__':
# Declaring array and deleting value
LA = [0,0,0]
n = len(LA)
print("Array Before Deletion: ")
for x in range(len(LA)):
LA.append(x)
LA[x] = x + 3
print("LA", [x], " = " , LA[x])
# delete the value if exists
# or show error it does not exist in the list
for x in range(1, n-1):
LA[x] = LA[x+1]
n = n-1
print("Array After Deletion: ")
for x in range(n):
print("LA", [x], " = " , LA[x])
Output
Array Before Deletion: LA [0] = 3 LA [1] = 4 LA [2] = 5 Array After Deletion: LA [0] = 3 LA [1] = 5
Search Operation
Searching an element in the array using a key; The key element sequentially compares every value in the array to check if the key is present in the array or not.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to find an element with a value of ITEM using sequential search.
1. Start 2. Set J = 0 3. Repeat steps 4 and 5 while J < N 4. IF LA[J] is equal ITEM THEN GOTO STEP 6 5. Set J = J +1 6. PRINT J, ITEM 7. Stop
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
void main(){
int LA[] = {1,3,5,7,8};
int item = 5, n = 5;
int i = 0, j = 0;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
for(i = 0; i<n; i++) {
if( LA[i] == item ) {
printf("Found element %d at position %d\n", item, i+1);
}
}
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 Found element 5 at position 3
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 5, n = 5;
int i = 0;
cout << "The original array elements are : " <<endl;
for(i = 0; i<n; i++) {
cout << "LA[" << i << "] = " << LA[i] << endl;
}
for(i = 0; i<n; i++) {
if( LA[i] == item ) {
cout << "Found element " << item << " at position " << i+1 <<endl;
}
}
return 0;
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 Found element 5 at position 3
public class ArrayDemo{
public static void main(String []args){
int LA[] = new int[5];
System.out.println("Array:");
for(int i = 0; i < 5; i++) {
LA[i] = i + 3;
System.out.println("LA[" + i + "] = " + LA[i]);
}
for(int i = 0; i < 5; i++) {
if(LA[i] == 6)
System.out.println("Element " + 6 + " is found at index " + i);
}
}
}
Output
Array: LA[0] = 3 LA[1] = 4 LA[2] = 5 LA[3] = 6 LA[4] = 7 Element 6 is found at index 3
#search operation using python
def findElement(arr, n, value):
for i in range(n):
if (arr[i] == value):
return i
# If the key is not found
return -1
# Driver's code
if __name__ == '__main__':
LA = [1,3,5,7,8]
print("Array element are: ")
for x in range(len(LA)):
print("LA", [x], " = ", LA[x])
value = 5
n = len(LA)
# element found using search operation
index = findElement(LA, n, value)
if index != -1:
print("Element", value, "Found at position = " + str(index + 1))
else:
print("Element not found")
Output
Array element are: LA [0] = 1 LA [1] = 3 LA [2] = 5 LA [3] = 7 LA [4] = 8 Element 5 Found at position = 3
Traversal Operation
This operation traverses through all the elements of an array. We use loop statements to carry this out.
Algorithm
Following is the algorithm to traverse through all the elements present in a Linear Array −
1 Start 2. Initialize an Array of certain size and datatype. 3. Initialize another variable i with 0. 4. Print the ith value in the array and increment i. 5. Repeat Step 4 until the end of the array is reached. 6. End
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
cout << "The original array elements are:\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
Output
The original array elements are: LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
Output
The array elements are: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 5 LA[4] = 6
# Python code to iterate over a array using python
LA = [1, 3, 5, 7, 8]
# length of the elements
length = len(LA)
# Traversing the elements using For loop and range
# same as 'for x in range(len(array))'
print("Array elements are: ")
for x in range(length):
print("LA", [x], " = ", LA[x])
Output
Array elements are: LA [0] = 1 LA [1] = 3 LA [2] = 5 LA [3] = 7 LA [4] = 8
Update Operation
Update operation refers to updating an existing element from the array at a given index.
Algorithm
Consider LA is a linear array with N elements and K is a positive integer such that K<=N. Following is the algorithm to update an element available at the Kth position of LA.
1. Start 2. Set LA[K-1] = ITEM 3. Stop
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
void main(){
int LA[] = {1,3,5,7,8};
int k = 3, n = 5, item = 10;
int i, j;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
LA[k-1] = item;
printf("The array elements after updation :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 The array elements after updation : LA[0] = 1 LA[1] = 3 LA[2] = 10 LA[3] = 7 LA[4] = 8
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int item = 10, k = 3, n = 5;
int i = 0, j = n;
cout << "The original array elements are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
LA[2] = item;
cout << "The array elements after updation are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8 The array elements after updation are : LA[0] = 1 LA[1] = 3 LA[2] = 10 LA[3] = 7 LA[4] = 8
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
int item = 15;
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
LA[3] = item;
System.out.println("The array elements after updation are: ");
for(int i = 0; i < 5; i++)
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
Output
The array elements are: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 5 LA[4] = 6 The array elements after updation are: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 15 LA[4] = 6
#update operation using python
#Declaring array elements
LA = [1,3,5,7,8]
#before updation
print("The original array elements are :");
for x in range(len(LA)):
print("LA", [x], " = ", LA[x])
#after updation
LA[2] = 10
print("The array elements after updation are: ")
for x in range(len(LA)):
print("LA", [x], " = ", LA[x])
Output
The original array elements are : LA [0] = 1 LA [1] = 3 LA [2] = 5 LA [3] = 7 LA [4] = 8 The array elements after updation are: LA [0] = 1 LA [1] = 3 LA [2] = 10 LA [3] = 7 LA [4] = 8
Display Operation
This operation displays all the elements in the entire array using a print statement.
Algorithm
1. Start 2. Print all the elements in the Array 3. Stop
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int main(){
int LA[] = {1,3,5,7,8};
int n = 5;
int i;
printf("The original array elements are :\n");
for(i = 0; i<n; i++) {
printf("LA[%d] = %d \n", i, LA[i]);
}
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
#include <iostream>
using namespace std;
int main(){
int LA[] = {1,3,5,7,8};
int n = 5;
int i;
cout << "The original array elements are :\n";
for(i = 0; i<n; i++)
cout << "LA[" << i << "] = " << LA[i] << endl;
return 0;
}
Output
The original array elements are : LA[0] = 1 LA[1] = 3 LA[2] = 5 LA[3] = 7 LA[4] = 8
public class ArrayDemo {
public static void main(String []args) {
int LA[] = new int[5];
System.out.println("The array elements are: ");
for(int i = 0; i < 5; i++) {
LA[i] = i + 2;
System.out.println("LA[" + i + "] = " + LA[i]);
}
}
}
Output
The array elements are: LA[0] = 2 LA[1] = 3 LA[2] = 4 LA[3] = 5 LA[4] = 6
#Display operation using python
#Display operation using python
#Declaring array elements
LA = [2,3,4,5,6]
#Displaying the array
print("The array elements are: ")
for x in range(len(LA)):
print("LA", [x], " = " , LA[x])
Output
The array elements are: LA [0] = 2 LA [1] = 3 LA [2] = 4 LA [3] = 5 LA [4] = 6
Linked List Data Structure
If arrays accommodate similar types of data types, linked lists consist of elements with different data types that are also arranged sequentially.
But how are these linked lists created?
A linked list is a collection of nodes connected together via links. These nodes consist of the data to be stored and a pointer to the address of the next node within the linked list. In the case of arrays, the size is limited to the definition, but in linked lists, there is no defined size. Any amount of data can be stored in it and can be deleted from it.
There are three types of linked lists −
Singly Linked List − The nodes only point to the address of the next node in the list.
Doubly Linked List − The nodes point to the addresses of both previous and next nodes.
Circular Linked List − The last node in the list will point to the first node in the list. It can either be singly linked or doubly linked.
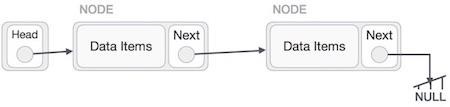
Linked List Representation
Linked list can be visualized as a chain of nodes, where every node points to the next node.
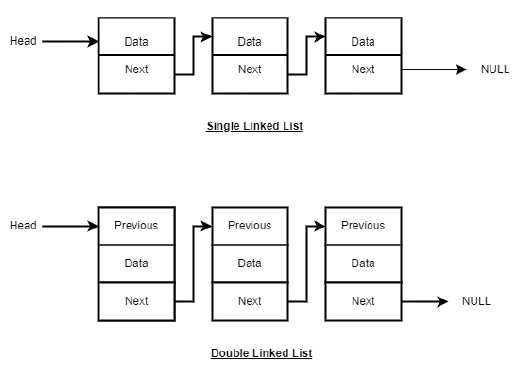
As per the above illustration, following are the important points to be considered.
Linked List contains a link element called first (head).
Each link carries a data field(s) and a link field called next.
Each link is linked with its next link using its next link.
Last link carries a link as null to mark the end of the list.
Types of Linked List
Following are the various types of linked list.
Singly Linked Lists
Singly linked lists contain two buckets in one node; one bucket holds the data and the other bucket holds the address of the next node of the list. Traversals can be done in one direction only as there is only a single link between two nodes of the same list.

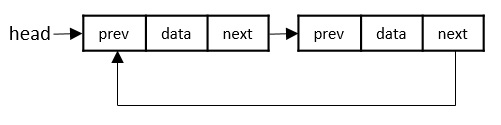
Doubly Linked Lists
Doubly Linked Lists contain three buckets in one node; one bucket holds the data and the other buckets hold the addresses of the previous and next nodes in the list. The list is traversed twice as the nodes in the list are connected to each other from both sides.

Circular Linked Lists
Circular linked lists can exist in both singly linked list and doubly linked list.
Since the last node and the first node of the circular linked list are connected, the traversal in this linked list will go on forever until it is broken.
Basic Operations in the Linked Lists
The basic operations in the linked lists are insertion, deletion, searching, display, and deleting an element at a given key. These operations are performed on Singly Linked Lists as given below −
Insertion − Adds an element at the beginning of the list.
Deletion − Deletes an element at the beginning of the list.
Display − Displays the complete list.
Search − Searches an element using the given key.
Delete − Deletes an element using the given key.
Insertion Operation
Adding a new node in linked list is a more than one step activity. We shall learn this with diagrams here. First, create a node using the same structure and find the location where it has to be inserted.
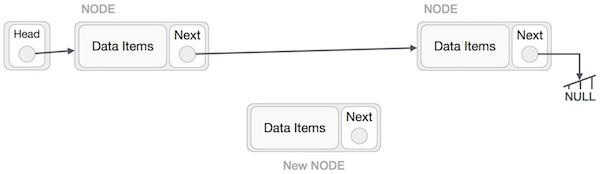
Imagine that we are inserting a node B (NewNode), between A (LeftNode) and C (RightNode). Then point B.next to C −
NewNode.next −> RightNode;
It should look like this −
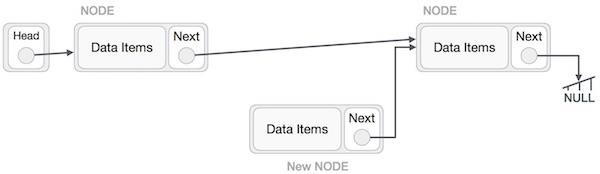
Now, the next node at the left should point to the new node.
LeftNode.next −> NewNode;
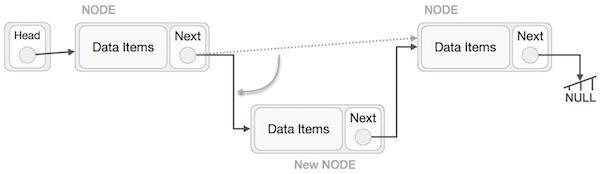
This will put the new node in the middle of the two. The new list should look like this −
Insertion in linked list can be done in three different ways. They are explained as follows −
Insertion at Beginning
In this operation, we are adding an element at the beginning of the list.
Algorithm
1. START 2. Create a node to store the data 3. Check if the list is empty 4. If the list is empty, add the data to the node and assign the head pointer to it. 5 If the list is not empty, add the data to a node and link to the current head. Assign the head to the newly added node. 6. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
printf("Linked List: ");
// print list
printList();
}
Output
Linked List: [ 50 44 30 22 12 ]
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
cout << "\n[";
//start from the beginning
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
cout << "]";
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
int main(){
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
cout << "Linked List: ";
// print list
printList();
}
Output
Linked List: [ 50 44 30 22 12 ]
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
insertatbegin(33);
System.out.println("Linked List: ");
// print list
printList();
}
}
Output
Linked List: [33 50 44 30 22 12 ]
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class SLL:
def __init__(self):
self.head = None
# Print the linked list
def listprint(self):
printval = self.head
print("Linked List: ")
while printval is not None:
print (printval.data)
printval = printval.next
def AddAtBeginning(self,newdata):
NewNode = Node(newdata)
# Update the new nodes next val to existing node
NewNode.next = self.head
self.head = NewNode
l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")
l1.head.next = e2
e2.next = e3
l1.AddAtBeginning("122")
l1.listprint()
Output
Linked List: 122 731 672 63
Insertion at Ending
In this operation, we are adding an element at the ending of the list.
Algorithm
1. START 2. Create a new node and assign the data 3. Find the last node 4. Point the last node to new node 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void insertatend(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
struct node *linkedlist = head;
// point it to old first node
while(linkedlist->next != NULL)
linkedlist = linkedlist->next;
//point first to new first node
linkedlist->next = lk;
}
void main(){
int k=0;
insertatbegin(12);
insertatend(22);
insertatend(30);
insertatend(44);
insertatend(50);
printf("Linked List: ");
// print list
printList();
}
Output
Linked List: [ 12 22 30 44 50 ]
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
cout << "\n[";
//start from the beginning
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
cout << "]";
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void insertatend(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
struct node *linkedlist = head;
// point it to old first node
while(linkedlist->next != NULL)
linkedlist = linkedlist->next;
//point first to new first node
linkedlist->next = lk;
}
int main(){
insertatbegin(12);
insertatend(22);
insertatbegin(30);
insertatend(44);
insertatbegin(50);
cout << "Linked List: ";
// print list
printList();
}
Output
Linked List: [ 50 30 12 22 44 ]
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
static void insertatend(int data) {
//create a link
node lk = new node(data);
node linkedlist = head;
// point it to old first node
while(linkedlist.next != null)
linkedlist = linkedlist.next;
//point first to new first node
linkedlist.next = lk;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatend(44);
insertatend(50);
insertatend(33);
System.out.println("Linked List: ");
// print list
printList();
}
}
Output
Linked List: [ 30 22 12 44 50 33 ]
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class LL:
def __init__(self):
self.head = None
def listprint(self):
val = self.head
print("Linked List:")
while val is not None:
print(val.data)
val = val.next
l1 = LL()
l1.head = Node("23")
l2 = Node("12")
l3 = Node("7")
l4 = Node("14")
l5 = Node("61")
# Linking the first Node to second node
l1.head.next = l2
# Linking the second Node to third node
l2.next = l3
l3.next = l4
l4.next = l5
l1.listprint()
Output
Linked List: 23 12 7 14 61
Insertion at a Given Position
In this operation, we are adding an element at any position within the list.
Algorithm
1. START 2. Create a new node and assign data to it 3. Iterate until the node at position is found 4. Point first to new first node 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void insertafternode(struct node *list, int data){
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
lk->next = list->next;
list->next = lk;
}
void main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertafternode(head->next, 30);
printf("Linked List: ");
// print list
printList();
}
Output
Linked List: [ 22 12 30 ]
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
cout << "\n[";
//start from the beginning
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
cout << "]";
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void insertafternode(struct node *list, int data){
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
lk->next = list->next;
list->next = lk;
}
int main(){
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertafternode(head->next,44);
insertafternode(head->next->next, 50);
cout << "Linked List: ";
// print list
printList();
}
Output
Linked List: [ 30 22 44 50 12 ]
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
static void insertafternode(node list, int data) {
node lk = new node(data);
lk.next = list.next;
list.next = lk;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertafternode(head.next, 50);
insertafternode(head.next.next, 33);
System.out.println("Linked List: ");
// print list
printList();
}
}
Output
Linked List: [44 30 50 33 22 12 ]
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class SLL:
def __init__(self):
self.head = None
# Print the linked list
def listprint(self):
printval = self.head
print("Linked List: ")
while printval is not None:
print (printval.data)
printval = printval.next
# Function to add node
def InsertAtPos(self,nodeatpos,newdata):
if nodeatpos is None:
print("The mentioned node is absent")
return
NewNode = Node(newdata)
NewNode.next = nodeatpos.next
nodeatpos.next = NewNode
l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")
l1.head.next = e2
e2.next = e3
l1.InsertAtPos(l1.head.next, "122")
l1.listprint()
Output
Linked List: 731 672 122 63
Deletion Operation
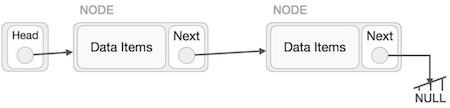
Deletion is also a more than one step process. We shall learn with pictorial representation. First, locate the target node to be removed, by using searching algorithms.

The left (previous) node of the target node now should point to the next node of the target node −
LeftNode.next > TargetNode.next;

This will remove the link that was pointing to the target node. Now, using the following code, we will remove what the target node is pointing at.
TargetNode.next > NULL;

We need to use the deleted node. We can keep that in memory otherwise we can simply deallocate memory and wipe off the target node completely.

Similar steps should be taken if the node is being inserted at the beginning of the list. While inserting it at the end, the second last node of the list should point to the new node and the new node will point to NULL.
Deletion in linked lists is also performed in three different ways. They are as follows −
Deletion at Beginning
In this deletion operation of the linked, we are deleting an element from the beginning of the list. For this, we point the head to the second node.
Algorithm
1. START 2. Assign the head pointer to the next node in the list 3. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void deleteatbegin(){
head = head->next;
}
int main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(40);
insertatbegin(55);
printf("Linked List: ");
// print list
printList();
deleteatbegin();
printf("\nLinked List after deletion: ");
// print list
printList();
}
Output
Linked List: [ 55 40 30 22 12 ] Linked List after deletion: [ 40 30 22 12 ]
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
cout << "\n[";
//start from the beginning
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
cout << "]";
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void deleteatbegin(){
head = head->next;
}
int main(){
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
cout << "Linked List: ";
// print list
printList();
deleteatbegin();
cout << "Linked List after deletion: ";
printList();
}
Output
Linked List: [ 50 44 30 22 12 ] Linked List after deletion: [ 44 30 22 12 ]
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
static void deleteatbegin() {
head = head.next;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
insertatbegin(33);
System.out.println("Linked List: ");
// print list
printList();
deleteatbegin();
System.out.println("\nLinked List after deletion: ");
// print list
printList();
}
}
Output
Linked List: [ 33 50 44 30 22 12 ] Linked List after deletion: [50 44 30 22 12 ]
#python code for deletion at beginning using linked list.
from typing import Optional
class Node:
def __init__(self, data: int, next: Optional['Node'] = None):
self.data = data
self.next = next
class LinkedList:
def __init__(self):
self.head = None
#display the list
def print_list(self):
p = self.head
print("\n[", end="")
while p:
print(f" {p.data} ", end="")
p = p.next
print("]")
#Insertion at the beginning
def insert_at_begin(self, data: int):
lk = Node(data)
#point it to old first node
lk.next = self.head
#point firt to new first node
self.head = lk
def delete_at_begin(self):
self.head = self.head.next
if __name__ == "__main__":
linked_list = LinkedList()
linked_list.insert_at_begin(12)
linked_list.insert_at_begin(22)
linked_list.insert_at_begin(30)
linked_list.insert_at_begin(44)
linked_list.insert_at_begin(50)
#print list
print("Linked List: ", end="")
linked_list.print_list()
linked_list.delete_at_begin()
print("Linked List after deletion: ", end="")
linked_list.print_list()
Output
Linked List: [ 50 44 30 22 12 ] Linked List after deletion: [ 44 30 22 12 ]
Deletion at Ending
In this deletion operation of the linked, we are deleting an element from the ending of the list.
Algorithm
1. START 2. Iterate until you find the second last element in the list. 3. Assign NULL to the second last element in the list. 4. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void deleteatend(){
struct node *linkedlist = head;
while (linkedlist->next->next != NULL)
linkedlist = linkedlist->next;
linkedlist->next = NULL;
}
void main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(40);
insertatbegin(55);
printf("Linked List: ");
// print list
printList();
deleteatend();
printf("\nLinked List after deletion: ");
// print list
printList();
}
Output
Linked List: [ 55 40 30 22 12 ] Linked List after deletion: [ 55 40 30 22 ]
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// Displaying the list
void printList(){
struct node *p = head;
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
}
// Insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void deleteatend(){
struct node *linkedlist = head;
while (linkedlist->next->next != NULL)
linkedlist = linkedlist->next;
linkedlist->next = NULL;
}
int main(){
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
cout << "Linked List: ";
// print list
printList();
deleteatend();
cout << "\nLinked List after deletion: ";
printList();
}
Output
Linked List: 50 44 30 22 12 Linked List after deletion: 50 44 30 22
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
static void deleteatend() {
node linkedlist = head;
while (linkedlist.next.next != null)
linkedlist = linkedlist.next;
linkedlist.next = null;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
insertatbegin(33);
System.out.println("Linked List: ");
// print list
printList();
//deleteatbegin();
deleteatend();
System.out.println("\nLinked List after deletion: ");
// print list
printList();
}
}
Output
Linked List: [ 33 50 44 30 22 12 ] Linked List after deletion: [ 33 50 44 30 22 ]
#python code for deletion at beginning using linked list.
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
#Displaying the list
def printList(self):
p = self.head
print("\n[", end="")
while p != None:
print(" " + str(p.data) + " ", end="")
p = p.next
print("]")
#Insertion at the beginning
def insertatbegin(self, data):
#create a link
lk = Node(data)
#point it to old first node
lk.next = self.head
#point first to new first node
self.head = lk
def deleteatend(self):
linkedlist = self.head
while linkedlist.next.next != None:
linkedlist = linkedlist.next
linkedlist.next = None
if __name__ == "__main__":
linked_list = LinkedList()
linked_list.insertatbegin(12)
linked_list.insertatbegin(22)
linked_list.insertatbegin(30)
linked_list.insertatbegin(40)
linked_list.insertatbegin(55)
#print list
print("Linked List: ", end="")
linked_list.printList()
linked_list.deleteatend()
print("Linked List after deletion: ", end="")
linked_list.printList()
Output
Linked List: [ 55 40 30 22 12 ] Linked List after deletion: [ 55 40 30 22 ]
Deletion at a Given Position
In this deletion operation of the linked, we are deleting an element at any position of the list.
Algorithm
1. START 2. Iterate until find the current node at position in the list 3. Assign the adjacent node of current node in the list to its previous node. 4. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void deletenode(int key){
struct node *temp = head, *prev;
if (temp != NULL && temp->data == key) {
head = temp->next;
return;
}
// Find the key to be deleted
while (temp != NULL && temp->data != key) {
prev = temp;
temp = temp->next;
}
// If the key is not present
if (temp == NULL) return;
// Remove the node
prev->next = temp->next;
}
void main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(40);
insertatbegin(55);
printf("Linked List: ");
// print list
printList();
deletenode(30);
printf("\nLinked List after deletion: ");
// print list
printList();
}
Output
Linked List: [ 55 40 30 22 12 ] Linked List after deletion: [ 55 40 22 12 ]
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
cout << "\n[";
//start from the beginning
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
cout << "]";
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void deletenode(int key){
struct node *temp = head, *prev;
if (temp != NULL && temp->data == key) {
head = temp->next;
return;
}
// Find the key to be deleted
while (temp != NULL && temp->data != key) {
prev = temp;
temp = temp->next;
}
// If the key is not present
if (temp == NULL) return;
// Remove the node
prev->next = temp->next;
}
int main(){
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
cout << "Linked List: ";
// print list
printList();
deletenode(30);
cout << "Linked List after deletion: ";
printList();
}
Output
Linked List: [ 50 44 30 22 12 ]Linked List after deletion: [ 50 44 22 12 ]
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
static void deletenode(int key) {
node temp = head;
node prev = null;
if (temp != null && temp.data == key) {
head = temp.next;
return;
}
// Find the key to be deleted
while (temp != null && temp.data != key) {
prev = temp;
temp = temp.next;
}
// If the key is not present
if (temp == null) return;
// Remove the node
prev.next = temp.next;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
insertatbegin(33);
System.out.println("Linked List: ");
// print list
printList();
//deleteatbegin();
//deleteatend();
deletenode(12);
System.out.println("\nLinked List after deletion: ");
// print list
printList();
}
}
Output
Linked List: [ 33 50 44 30 22 12 ] Linked List after deletion: [ 33 50 44 30 22 ]
#python code for deletion at given position using linked list.
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
# display the list
def printList(self):
p = self.head
print("\n[", end="")
#start from the beginning
while(p != None):
print(" ", p.data, " ", end="")
p = p.next
print("]")
#insertion at the beginning
def insertatbegin(self, data):
#create a link
lk = Node(data)
# point it to old first node
lk.next = self.head
#point first to new first node
self.head = lk
def deletenode(self, key):
temp = self.head
if (temp != None and temp.data == key):
self.head = temp.next
return
# Find the key to be deleted
while (temp != None and temp.data != key):
prev = temp
temp = temp.next
# If the key is not present
if (temp == None):
return
# Remove the node
prev.next = temp.next
llist = LinkedList()
llist.insertatbegin(12)
llist.insertatbegin(22)
llist.insertatbegin(30)
llist.insertatbegin(40)
llist.insertatbegin(55)
print("Original Linked List: ", end="")
# print list
llist.printList()
llist.deletenode(30)
print("\nLinked List after deletion: ", end="")
# print list
llist.printList()
Output
Linked List: [ 55 40 30 22 12 ] Linked List after deletion: [ 55 40 22 12 ]
Reverse Operation
This operation is a thorough one. We need to make the last node to be pointed by the head node and reverse the whole linked list.
First, we traverse to the end of the list. It should be pointing to NULL. Now, we shall make it point to its previous node −
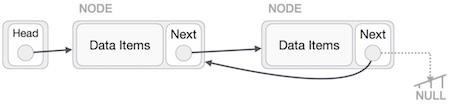
We have to make sure that the last node is not the last node. So we'll have some temp node, which looks like the head node pointing to the last node. Now, we shall make all left side nodes point to their previous nodes one by one.
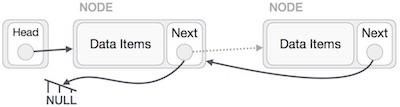
Except the node (first node) pointed by the head node, all nodes should point to their predecessor, making them their new successor. The first node will point to NULL.
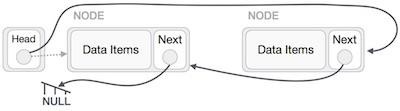
We'll make the head node point to the new first node by using the temp node.
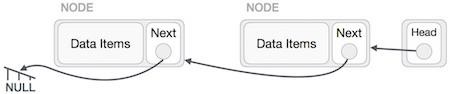
Algorithm
Step by step process to reverse a linked list is as follows −
1 START 2. We use three pointers to perform the reversing: prev, next, head. 3. Point the current node to head and assign its next value to the prev node. 4. Iteratively repeat the step 3 for all the nodes in the list. 5. Assign head to the prev node.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void reverseList(struct node** head){
struct node *prev = NULL, *cur=*head, *tmp;
while(cur!= NULL) {
tmp = cur->next;
cur->next = prev;
prev = cur;
cur = tmp;
}
*head = prev;
}
void main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(40);
insertatbegin(55);
printf("Linked List: ");
// print list
printList();
reverseList(&head);
printf("\nReversed Linked List: ");
printList();
}
Output
Linked List: [ 55 40 30 22 12 ] Reversed Linked List: [ 12 22 30 40 55 ]
#include <bits/stdc++.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void reverseList(struct node** head){
struct node *prev = NULL, *cur=*head, *tmp;
while(cur!= NULL) {
tmp = cur->next;
cur->next = prev;
prev = cur;
cur = tmp;
}
*head = prev;
}
int main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(40);
insertatbegin(55);
printf("Linked List: ");
// print list
printList();
reverseList(&head);
printf("\nReversed Linked List: ");
printList();
return 0;
}
Output
Linked List: [ 55 40 30 22 12 ] Reversed Linked List: [ 12 22 30 40 55 ]
public class Linked_List {
static Node head;
static class Node {
int data;
Node next;
Node (int value) {
data = value;
next = null;
}
}
// display the list
static void printList(Node node) {
System.out.print("\n[");
//start from the beginning
while(node != null) {
System.out.print(" " + node.data + " ");
node = node.next;
}
System.out.print("]");
}
static Node reverseList(Node head) {
Node prev = null;
Node cur = head;
Node temp = null;
while (cur != null) {
temp = cur.next;
cur.next = prev;
prev = cur;
cur = temp;
}
head = prev;
return head;
}
public static void main(String args[]) {
Linked_List list = new Linked_List();
list.head = new Node(33);
list.head.next = new Node(50);
list.head.next.next = new Node(44);
list.head.next.next.next = new Node(22);
list.head.next.next.next.next = new Node(12);
System.out.println("Linked List: ");
// print list
list.printList(head);
head = list.reverseList(head);
System.out.println("\nReversed linked list ");
list.printList(head);
}
}
Output
Linked List: [ 33 50 44 22 12 ] Reversed linked list [ 12 22 44 50 33 ]
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class SLL:
def __init__(self):
self.head = None
# Print the linked list
def listprint(self):
printval = self.head
print("Linked List: ")
while printval is not None:
print (printval.data)
printval = printval.next
def reverse(self):
prev = None
curr = self.head
while(curr is not None):
next = curr.next
curr.next = prev
prev = curr
curr = next
self.head = prev
l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")
l1.head.next = e2
e2.next = e3
l1.listprint()
l1.reverse()
print("After reversing: ")
l1.listprint()
Output
Linked List: 731 672 63 After reversing: Linked List: 63 672 731
Search Operation
Searching for an element in the list using a key element. This operation is done in the same way as array search; comparing every element in the list with the key element given.
Algorithm
1 START 2 If the list is not empty, iteratively check if the list contains the key 3 If the key element is not present in the list, unsuccessful search 4 END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
int searchlist(int key){
struct node *temp = head;
while(temp != NULL) {
if (temp->data == key) {
return 1;
}
temp=temp->next;
}
return 0;
}
void main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(40);
insertatbegin(55);
printf("Linked List: ");
// print list
printList();
k = searchlist(30);
if (k == 1)
printf("\nElement is found");
else
printf("\nElement is not present in the list");
}
Output
Linked List: [ 55 40 30 22 12 ] Element is found
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
cout << "\n[";
//start from the beginning
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
cout << "]";
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
int searchlist(int key){
struct node *temp = head;
while(temp != NULL) {
if (temp->data == key) {
return 1;
}
temp=temp->next;
}
return 0;
}
int main(){
int k = 0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
cout << "Linked List: ";
// print list
printList();
k = searchlist(16);
if (k == 1)
cout << "\nElement is found";
else
cout << "\nElement is not present in the list";
}
Output
Linked List: [ 50 44 30 22 12 ] Element is not present in the list
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
static int searchlist(int key) {
node temp = head;
while(temp != null) {
if (temp.data == key) {
return 1;
}
temp=temp.next;
}
return 0;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
insertatbegin(33);
System.out.println("Linked List: ");
// print list
printList();
k = searchlist(44);
if (k == 1)
System.out.println("\nElement is found");
else
System.out.println("\nElement is not present in the list");
}
}
Output
Linked List: [33 50 44 30 22 12 ] Element is found
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class SLL:
def __init__(self):
self.head = None
def search(self, x):
count = 0
# Initialize current to head
current = self.head
# loop till current not equal to None
while current != None:
if current.data == x:
print("data found")
count = count + 1
current = current.next
if count == 0:
print("Data Not found")
l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")
l1.head.next = e2
e2.next = e3
l1.search("63")
Output
data found
Traversal Operation
The traversal operation walks through all the elements of the list in an order and displays the elements in that order.
Algorithm
1. START 2. While the list is not empty and did not reach the end of the list, print the data in each node 3. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
printf("Linked List: ");
// print list
printList();
}
Output
Linked List: [ 30 22 12 ]
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// Displaying the list
void printList(){
struct node *p = head;
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
}
// Insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
int main(){
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
cout << "Linked List: ";
// print list
printList();
}
Output
Linked List: 50 44 30 22 12
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatbegin(30);
insertatbegin(44);
insertatbegin(50);
insertatbegin(33);
System.out.println("Linked List: ");
// print list
printList();
}
}
Output
Linked List: [ 33 50 44 30 22 12 ]
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class SLL:
def __init__(self):
self.head = None
# Print the linked list
def listprint(self):
printval = self.head
print("Linked List: ")
while printval is not None:
print (printval.data)
printval = printval.next
l1 = SLL()
l1.head = Node("731")
e2 = Node("672")
e3 = Node("63")
l1.head.next = e2
e2.next = e3
l1.listprint()
Output
Linked List: 731 672 63
Complete implementation
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
printf("\n[");
//start from the beginning
while(p != NULL) {
printf(" %d ",p->data);
p = p->next;
}
printf("]");
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void insertatend(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
struct node *linkedlist = head;
// point it to old first node
while(linkedlist->next != NULL)
linkedlist = linkedlist->next;
//point first to new first node
linkedlist->next = lk;
}
void insertafternode(struct node *list, int data){
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
lk->next = list->next;
list->next = lk;
}
void deleteatbegin(){
head = head->next;
}
void deleteatend(){
struct node *linkedlist = head;
while (linkedlist->next->next != NULL)
linkedlist = linkedlist->next;
linkedlist->next = NULL;
}
void deletenode(int key){
struct node *temp = head, *prev;
if (temp != NULL && temp->data == key) {
head = temp->next;
return;
}
// Find the key to be deleted
while (temp != NULL && temp->data != key) {
prev = temp;
temp = temp->next;
}
// If the key is not present
if (temp == NULL) return;
// Remove the node
prev->next = temp->next;
}
int searchlist(int key){
struct node *temp = head;
while(temp != NULL) {
if (temp->data == key) {
return 1;
}
temp=temp->next;
}
return 0;
}
void main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatend(30);
insertatend(44);
insertatbegin(50);
insertafternode(head->next->next, 33);
printf("Linked List: ");
// print list
printList();
deleteatbegin();
deleteatend();
deletenode(12);
printf("\nLinked List after deletion: ");
// print list
printList();
insertatbegin(4);
insertatbegin(16);
printf("\nUpdated Linked List: ");
printList();
k = searchlist(16);
if (k == 1)
printf("\nElement is found");
else
printf("\nElement is not present in the list");
}
Output
Linked List: [ 50 22 12 33 30 44 ] Linked List after deletion: [ 22 33 30 ] Updated Linked List: [ 16 4 22 33 30 ] Element is found
#include <bits/stdc++.h>
#include <string>
using namespace std;
struct node {
int data;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
// display the list
void printList(){
struct node *p = head;
cout << "\n[";
//start from the beginning
while(p != NULL) {
cout << " " << p->data << " ";
p = p->next;
}
cout << "]";
}
//insertion at the beginning
void insertatbegin(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
// point it to old first node
lk->next = head;
//point first to new first node
head = lk;
}
void insertatend(int data){
//create a link
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
struct node *linkedlist = head;
// point it to old first node
while(linkedlist->next != NULL)
linkedlist = linkedlist->next;
//point first to new first node
linkedlist->next = lk;
}
void insertafternode(struct node *list, int data){
struct node *lk = (struct node*) malloc(sizeof(struct node));
lk->data = data;
lk->next = list->next;
list->next = lk;
}
void deleteatbegin(){
head = head->next;
}
void deleteatend(){
struct node *linkedlist = head;
while (linkedlist->next->next != NULL)
linkedlist = linkedlist->next;
linkedlist->next = NULL;
}
void deletenode(int key){
struct node *temp = head, *prev;
if (temp != NULL && temp->data == key) {
head = temp->next;
return;
}
// Find the key to be deleted
while (temp != NULL && temp->data != key) {
prev = temp;
temp = temp->next;
}
// If the key is not present
if (temp == NULL) return;
// Remove the node
prev->next = temp->next;
}
int searchlist(int key){
struct node *temp = head;
while(temp != NULL) {
if (temp->data == key) {
temp=temp->next;
return 1;
} else
return 0;
}
}
int main(){
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatend(30);
insertatend(44);
insertatbegin(50);
insertafternode(head->next->next, 33);
cout << "Linked List: ";
// print list
printList();
deleteatbegin();
deleteatend();
deletenode(12);
cout << "\nLinked List after deletion: ";
// print list
printList();
insertatbegin(4);
insertatbegin(16);
cout << "\nUpdated Linked List: ";
printList();
k = searchlist(16);
if (k == 1)
cout << "\nElement is found";
else
cout << "\nElement is not present in the list";
return 0;
}
Output
Linked List: [ 50 22 12 33 30 44 ] Linked List after deletion: [ 22 33 30 ] Updated Linked List: [ 16 4 22 33 30 ] Element is found
public class Linked_List {
static class node {
int data;
node next;
node (int value) {
data = value;
next = null;
}
}
static node head;
// display the list
static void printList() {
node p = head;
System.out.print("\n[");
//start from the beginning
while(p != null) {
System.out.print(" " + p.data + " ");
p = p.next;
}
System.out.print("]");
}
//insertion at the beginning
static void insertatbegin(int data) {
//create a link
node lk = new node(data);;
// point it to old first node
lk.next = head;
//point first to new first node
head = lk;
}
static void insertatend(int data) {
//create a link
node lk = new node(data);
node linkedlist = head;
// point it to old first node
while(linkedlist.next != null)
linkedlist = linkedlist.next;
//point first to new first node
linkedlist.next = lk;
}
static void insertafternode(node list, int data) {
node lk = new node(data);
lk.next = list.next;
list.next = lk;
}
static void deleteatbegin() {
head = head.next;
}
static void deleteatend() {
node linkedlist = head;
while (linkedlist.next.next != null)
linkedlist = linkedlist.next;
linkedlist.next = null;
}
static void deletenode(int key) {
node temp = head;
node prev = null;
if (temp != null && temp.data == key) {
head = temp.next;
return;
}
// Find the key to be deleted
while (temp != null && temp.data != key) {
prev = temp;
temp = temp.next;
}
// If the key is not present
if (temp == null) return;
// Remove the node
prev.next = temp.next;
}
static int searchlist(int key) {
node temp = head;
while(temp != null) {
if (temp.data == key) {
temp=temp.next;
return 1;
}
}
return 0;
}
public static void main(String args[]) {
int k=0;
insertatbegin(12);
insertatbegin(22);
insertatend(30);
insertatend(44);
insertatbegin(50);
insertafternode(head.next.next, 33);
System.out.println("Linked List: ");
// print list
printList();
deleteatbegin();
deleteatend();
deletenode(12);
System.out.println("\nLinked List after deletion: ");
// print list
printList();
insertatbegin(4);
insertatbegin(16);
System.out.println("\nUpdated Linked List: ");
printList();
k = searchlist(16);
if (k == 1)
System.out.println("\nElement is found");
else
System.out.println("\nElement is not present in the list");
}
}
Output
Linked List: [ 50 22 12 33 30 44 ] Linked List after deletion: [ 22 33 30 ] Updated Linked List: [ 16 4 22 33 30 ] Element is found
class LLNode:
def __init__(self, data=None):
self.data = data
self.next = None
class LL:
def __init__(self):
self.head = None
def listprint(self):
printval = self.head
while printval is not None:
print(printval.data)
printval = printval.next
def AddAtBeginning(self,newdata):
NewNode = LLNode(newdata)
# Update the new nodes next val to existing node
NewNode.next = self.head
self.head = NewNode
# Function to add node at a position
def InsertAtPos(self,nodeatpos,newdata):
if nodeatpos is None:
print("The mentioned node is absent")
return
NewNode = LLNode(newdata)
NewNode.next = nodeatpos.next
nodeatpos.next = NewNode
def reverse(self):
prev = None
curr = self.head
while(curr is not None):
next = curr.next
curr.next = prev
prev = curr
curr = next
self.head = prev
def search(self, x):
count = 0
# Initialize current to head
current = self.head
# loop till current not equal to None
while current != None:
if current.data == x:
print("data found")
count = count + 1
current = current.next
if count == 0:
print("Data Not found")
l1 = LL()
l1.head = LLNode("23")
l2 = LLNode("12")
l3 = LLNode("7")
l4 = LLNode("14")
l5 = LLNode("61")
# Linking the first Node to second node
l1.head.next = l2
# Linking the second Node to third node
l2.next = l3
l3.next = l4
l4.next = l5
print("Original Linked List: ")
l1.listprint()
l1.AddAtBeginning("45")
l1.InsertAtPos(l1.head.next.next, "4")
print("Updated Linked List:")
l1.listprint()
l1.reverse()
print("Reversed Linked List:")
l1.listprint()
l1.search("7")
Output
Original Linked List: 23 12 7 14 61 Updated Linked List: 45 23 12 4 7 14 61 Reversed Linked List: 61 14 7 4 12 23 45 data found
Doubly Linked List Data Structure
Doubly Linked List is a variation of Linked list in which navigation is possible in both ways, either forward and backward easily as compared to Single Linked List. Following are the important terms to understand the concept of doubly linked list.
Link − Each link of a linked list can store a data called an element.
Next − Each link of a linked list contains a link to the next link called Next.
Prev − Each link of a linked list contains a link to the previous link called Prev.
Linked List − A Linked List contains the connection link to the first link called First and to the last link called Last.
Doubly Linked List Representation
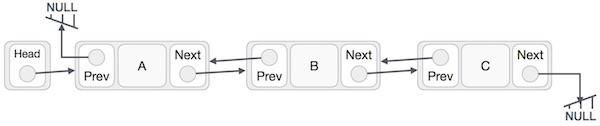
As per the above illustration, following are the important points to be considered.
Doubly Linked List contains a link element called first and last.
Each link carries a data field(s) and a link field called next.
Each link is linked with its next link using its next link.
Each link is linked with its previous link using its previous link.
The last link carries a link as null to mark the end of the list.
Basic Operations
Following are the basic operations supported by a list.
Insertion − Adds an element at the beginning of the list.
Deletion − Deletes an element at the beginning of the list.
Insert Last − Adds an element at the end of the list.
Delete Last − Deletes an element from the end of the list.
Insert After − Adds an element after an item of the list.
Delete − Deletes an element from the list using the key.
Display forward − Displays the complete list in a forward manner.
Display backward − Displays the complete list in a backward manner.
Insertion at the Beginning
In this operation, we create a new node with three compartments, one containing the data, the others containing the address of its previous and next nodes in the list. This new node is inserted at the beginning of the list.
Algorithm
1. START 2. Create a new node with three variables: prev, data, next. 3. Store the new data in the data variable 4. If the list is empty, make the new node as head. 5. Otherwise, link the address of the existing first node to the next variable of the new node, and assign null to the prev variable. 6. Point the head to the new node. 7. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the doubly linked list
void printList(){
struct node *ptr = head;
while(ptr != NULL) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
void main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nDoubly Linked List: ");
printList();
}
Output
Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10)
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the doubly linked list
void printList(){
struct node *ptr = head;
while(ptr != NULL) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nDoubly Linked List: ");
printList();
return 0;
}
Output
Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10)
//Java code for doubly linked list
import java.util.*;
class Node {
public int data;
public int key;
public Node next;
public Node prev;
public Node(int data, int key) {
this.data = data;
this.key = key;
this.next = null;
this.prev = null;
}
}
public class Main {
//this link always point to first Link
static Node head = null;
//this link always point to last Link
static Node last = null;
static Node current = null;
// is list empty
public static boolean is_empty() {
return head == null;
}
//display the doubly linked list
public static void print_list() {
Node ptr = head;
while (ptr != null) {
System.out.println("(" + ptr.key + "," + ptr.data + ")");
ptr = ptr.next;
}
}
//insert link at the first location
public static void insert_first(int key, int data) {
//create a link
Node link = new Node(data, key);
if (is_empty()) {
//make it the last link
last = link;
} else {
//update first prev link
head.prev = link;
}
//point it to old first link
link.next = head;
//point first to new first link
head = link;
}
public static void main(String[] args) {
insert_first(1, 10);
insert_first(2, 20);
insert_first(3, 30);
insert_first(4, 1);
insert_first(5, 40);
insert_first(6, 56);
System.out.println("\nDoubly Linked List: ");
print_list();
}
}
Output
Doubly Linked List: (6,56)(5,40)(4,1)(3,30)(2,20)(1,10)
#Python code for doubly linked list
class Node:
def __init__(self, data=None, key=None):
self.data = data
self.key = key
self.next = None
self.prev = None
#this link always point to first Link
head = None
#this link always point to last Link
last = None
current = None
#is list empty
def is_empty():
return head == None
#display the doubly linked list
def print_list():
ptr = head
while ptr != None:
print(f"({ptr.key},{ptr.data})")
ptr = ptr.next
#insert link at the first location
def insert_first(key, data):
global head, last
#create a link
link = Node(data, key)
if is_empty():
#make it the last link
last = link
else:
#update first prev link
head.prev = link
#point it to old first link
link.next = head
#point first to new first link
head = link
insert_first(1,10)
insert_first(2,20)
insert_first(3,30)
insert_first(4,1)
insert_first(5,40)
insert_first(6,56)
print("\nDoubly Linked List: ")
print_list()
Output
Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10)
Deletion at the Beginning
This deletion operation deletes the existing first nodes in the doubly linked list. The head is shifted to the next node and the link is removed.
Algorithm
1. START 2. Check the status of the doubly linked list 3. If the list is empty, deletion is not possible 4. If the list is not empty, the head pointer is shifted to the next node. 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the doubly linked list
void printList(){
struct node *ptr = head;
while(ptr != NULL) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL) {
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}
void main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nDoubly Linked List: ");
printList();
printf("\nList after deleting first record: ");
deleteFirst();
printList();
}
Output
Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) List after deleting first record: (5,40) (4,1) (3,30) (2,20) (1,10)
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the doubly linked list
void printList(){
struct node *ptr = head;
while(ptr != NULL) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL) {
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nDoubly Linked List: ");
printList();
printf("\nList after deleting first record: ");
deleteFirst();
printList();
return 0;
}
Output
Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) List after deleting first record: (5,40) (4,1) (3,30) (2,20) (1,10)
//Java code for doubly linked list
import java.util.*;
class Node {
public int data;
public int key;
public Node next;
public Node prev;
public Node(int data, int key) {
this.data = data;
this.key = key;
this.next = null;
this.prev = null;
}
}
public class Main {
//this link always point to first Link
public static Node head = null;
//this link always point to last Link
public static Node last = null;
//this link always point to current Link
public static Node current = null;
//is list empty
public static boolean isEmpty() {
return head == null;
}
//display the doubly linked list
public static void printList() {
Node ptr = head;
while (ptr != null) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.next;
}
}
//insert link at the first location
public static void insertFirst(int key, int data) {
//create a link
Node link = new Node(data, key);
if (isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head.prev = link;
}
//point it to old first link
link.next = head;
head = link;
}
//delete the first item
public static Node deleteFirst() {
//save reference to first link
Node tempLink = head;
//if only one link
if (head.next == null) {
last = null;
} else {
head.next.prev = null;
}
head = head.next;
//return the deleted link
return tempLink;
}
public static void main(String[] args) {
insertFirst(1, 10);
insertFirst(2, 20);
insertFirst(3, 30);
insertFirst(4, 1);
insertFirst(5, 40);
insertFirst(6, 56);
System.out.print("\nDoubly Linked List: ");
printList();
System.out.print("\nList after deleting first record: ");
deleteFirst();
printList();
}
}
Output
Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) List after deleting first record: (5,40) (4,1) (3,30) (2,20) (1,10)
#Python code for doubly linked list
class Node:
def __init__(self, data=None, key=None):
self.data = data
self.key = key
self.next = None
self.prev = None
#this link always point to first Link
head = None
#this link always point to last Link
last = None
current = None
#is list empty
def isEmpty():
return head == None
#display the doubly linked list
def printList():
ptr = head
while ptr != None:
print(f"({ptr.key},{ptr.data}) ", end="")
ptr = ptr.next
#insert link at the first location
def insertFirst(key, data):
#create a link
global head, last
link = Node(data, key)
if isEmpty():
#make it the last link
last = link
else:
#update first prev link
head.prev = link
#point it to old first link
link.next = head
head = link
#delete first item
def deleteFirst():
#save reference to first link
global head, last
tempLink = head
#if only one link
if head.next == None:
last = None
else:
head.next.prev = None
head = head.next
#return the deleted link
return tempLink
insertFirst(1,10)
insertFirst(2,20)
insertFirst(3,30)
insertFirst(4,1)
insertFirst(5,40)
insertFirst(6,56)
print("\nDoubly Linked List: ", end="")
printList()
print("\nList after deleting first record: ")
deleteFirst()
printList()
Output
Doubly Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) List after deleting first record: (5,40) (4,1) (3,30) (2,20) (1,10)
Insertion at the End
In this insertion operation, the new input node is added at the end of the doubly linked list; if the list is not empty. The head will be pointed to the new node, if the list is empty.
Algorithm
1. START 2. If the list is empty, add the node to the list and point the head to it. 3. If the list is not empty, find the last node of the list. 4. Create a link between the last node in the list and the new node. 5. The new node will point to NULL as it is the new last node. 6. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the doubly linked list
void printList(){
struct node *ptr = head;
while(ptr != NULL) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//insert link at the last location
void insertLast(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}
void main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertLast(5,40);
insertLast(6,56);
printf("\nDoubly Linked List: ");
printList();
}
Output
Doubly Linked List: (4,1) (3,30) (2,20) (1,10) (5,40) (6,56)
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the doubly linked list
void printList(){
struct node *ptr = head;
while(ptr != NULL) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//insert link at the last location
void insertLast(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertLast(5,40);
insertLast(6,56);
printf("\nDoubly Linked List: ");
printList();
return 0;
}
Output
Doubly Linked List: (4,1) (3,30) (2,20) (1,10) (5,40) (6,56)
import java.util.*;
class Node {
public int data;
public int key;
public Node next;
public Node prev;
public Node(int data, int key) {
this.data = data;
this.key = key;
this.next = null;
this.prev = null;
}
}
public class Main {
static Node head = null;
static Node last = null;
static Node current = null;
public static boolean isEmpty() {
return head == null;
}
public static void printList() {
Node ptr = head;
while (ptr != null) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.next;
}
}
public static void insertFirst(int key, int data) {
Node link = new Node(data, key);
if (isEmpty()) {
last = link;
} else {
head.prev = link;
}
link.next = head;
head = link;
}
public static void insertLast(int key, int data) {
Node link = new Node(data, key);
if (isEmpty()) {
last = link;
} else {
last.next = link;
link.prev = last;
}
last = link;
}
public static void main(String[] args) {
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertLast(5,40);
insertLast(6,56);
System.out.print("\nDoubly Linked List: ");
printList();
}
}
Output
Doubly Linked List: (4,1) (3,30) (2,20) (1,10) (5,40) (6,56)
class Node:
def __init__(self, data=None, key=None):
self.data = data
self.key = key
self.next = None
self.prev = None
head = None
last = None
current = None
def isEmpty():
return head == None
def printList():
ptr = head
while ptr != None:
print(f"({ptr.key},{ptr.data})", end=" ")
ptr = ptr.next
def insertFirst(key, data):
global head, last
link = Node(data, key)
if isEmpty():
last = link
else:
head.prev = link
link.next = head
head = link
def insertLast(key, data):
global head, last
link = Node(data, key)
if isEmpty():
last = link
else:
last.next = link
link.prev = last
last = link
insertFirst(1,10)
insertFirst(2,20)
insertFirst(3,30)
insertFirst(4,1)
insertLast(5,40)
insertLast(6,56)
print("\nDoubly Linked List: ", end="")
printList()
Output
Doubly Linked List: (4,1) (3,30) (2,20) (1,10) (5,40) (6,56)
Complete implementation
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the list in from first to last
void displayForward(){
//start from the beginning
struct node *ptr = head;
//navigate till the end of the list
printf("\n[ ");
while(ptr != NULL) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
printf(" ]");
}
//display the list from last to first
void displayBackward(){
//start from the last
struct node *ptr = last;
//navigate till the start of the list
printf("\n[ ");
while(ptr != NULL) {
//print data
printf("(%d,%d) ",ptr->key,ptr->data);
//move to next item
ptr = ptr ->prev;
printf(" ");
}
printf(" ]");
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//insert link at the last location
void insertLast(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL) {
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}
//delete link at the last location
struct node* deleteLast(){
//save reference to last link
struct node *tempLink = last;
//if only one link
if(head->next == NULL) {
head = NULL;
} else {
last->prev->next = NULL;
}
last = last->prev;
//return the deleted link
return tempLink;
}
//delete a link with given key
struct node* delete(int key){
//start from the first link
struct node* current = head;
struct node* previous = NULL;
//if list is empty
if(head == NULL) {
return NULL;
}
//navigate through list
while(current->key != key) {
//if it is last node
if(current->next == NULL) {
return NULL;
} else {
//store reference to current link
previous = current;
//move to next link
current = current->next;
}
}
//found a match, update the link
if(current == head) {
//change first to point to next link
head = head->next;
} else {
//bypass the current link
current->prev->next = current->next;
}
if(current == last) {
//change last to point to prev link
last = current->prev;
} else {
current->next->prev = current->prev;
}
return current;
}
bool insertAfter(int key, int newKey, int data){
//start from the first link
struct node *current = head;
//if list is empty
if(head == NULL) {
return false;
}
//navigate through list
while(current->key != key) {
//if it is last node
if(current->next == NULL) {
return false;
} else {
//move to next link
current = current->next;
}
}
//create a link
struct node *newLink = (struct node*) malloc(sizeof(struct node));
newLink->key = key;
newLink->data = data;
if(current == last) {
newLink->next = NULL;
last = newLink;
} else {
newLink->next = current->next;
current->next->prev = newLink;
}
newLink->prev = current;
current->next = newLink;
return true;
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nList (First to Last): ");
displayForward();
printf("\n");
printf("\nList (Last to first): ");
displayBackward();
printf("\nList , after deleting first record: ");
deleteFirst();
displayForward();
printf("\nList , after deleting last record: ");
deleteLast();
displayForward();
printf("\nList , insert after key(4) : ");
insertAfter(4,7, 13);
displayForward();
printf("\nList , after delete key(4) : ");
delete(4);
displayForward();
}
Output
List (First to Last):
[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]
List (Last to first):
[ (1,10) (2,20) (3,30) (4,1) (5,40) (6,56) ]
List , after deleting first record:
[ (5,40) (4,1) (3,30) (2,20) (1,10) ]
List , after deleting last record:
[ (5,40) (4,1) (3,30) (2,20) ]
List , insert after key(4) :
[ (5,40) (4,1) (4,13) (3,30) (2,20) ]
List , after delete key(4) :
[ (5,40) (4,13) (3,30) (2,20) ]
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
using namespace std;
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the list in from first to last
void displayForward(){
//start from the beginning
struct node *ptr = head;
//navigate till the end of the list
cout << "\n[ ";
while(ptr != NULL) {
cout << "(" << ptr->key << "," << ptr->data << ")";
ptr = ptr->next;
}
cout << " ]" << endl;
}
//display the list from last to first
void displayBackward(){
//start from the last
struct node *ptr = last;
//navigate till the start of the list
cout << "\n[ ";
while(ptr != NULL) {
//print data
cout << "(" << ptr->key << "," << ptr->data << ")";
//move to next item
ptr = ptr ->prev;
cout << " ";
}
cout << " ]" << endl;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//insert link at the last location
void insertLast(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL) {
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}
//delete link at the last location
struct node* deleteLast(){
//save reference to last link
struct node *tempLink = last;
//if only one link
if(head->next == NULL) {
head = NULL;
} else {
last->prev->next = NULL;
}
last = last->prev;
//return the deleted link
return tempLink;
}
//delete a link with given key
struct node* deletenode(int key){
//start from the first link
struct node* current = head;
struct node* previous = NULL;
//if list is empty
if(head == NULL) {
return NULL;
}
//navigate through list
while(current->key != key) {
//if it is last node
if(current->next == NULL) {
return NULL;
} else {
//store reference to current link
previous = current;
//move to next link
current = current->next;
}
}
//found a match, update the link
if(current == head) {
//change first to point to next link
head = head->next;
} else {
//bypass the current link
current->prev->next = current->next;
}
if(current == last) {
//change last to point to prev link
last = current->prev;
} else {
current->next->prev = current->prev;
}
return current;
}
bool insertAfter(int key, int newKey, int data){
//start from the first link
struct node *current = head;
//if list is empty
if(head == NULL) {
return false;
}
//navigate through list
while(current->key != key) {
//if it is last node
if(current->next == NULL) {
return false;
} else {
//move to next link
current = current->next;
}
}
//create a link
struct node *newLink = (struct node*) malloc(sizeof(struct node));
newLink->key = key;
newLink->data = data;
if(current == last) {
newLink->next = NULL;
last = newLink;
} else {
newLink->next = current->next;
current->next->prev = newLink;
}
newLink->prev = current;
current->next = newLink;
return true;
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nList (First to Last): ");
displayForward();
printf("\n");
printf("\nList (Last to first): ");
displayBackward();
printf("\nList , after deleting first record: ");
deleteFirst();
displayForward();
printf("\nList , after deleting last record: ");
deleteLast();
displayForward();
printf("\nList , insert after key(4) : ");
insertAfter(4, 7, 13);
displayForward();
printf("\nList , after delete key(4) : ");
deletenode(4);
displayForward();
return 0;
}
Output
List (First to Last):
[ (6, 56) (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ]
List (Last to First):
[ (1, 10) (2, 20) (3, 30) (4, 1) (5, 40) (6, 56) ]
List, after deleting first record:
[ (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ]
List, after deleting last record:
[ (5, 40) (4, 1) (3, 30) (2, 20) ]
List, insert after key(4):
[ (5, 40) (4, 1) (7, 13) (3, 30) (2, 20) ]
List, after delete key(4):
[ (5, 40) (7, 13) (3, 30) (2, 20) ]
class Node {
int data;
int key;
Node next;
Node prev;
public Node(int key, int data) {
this.key = key;
this.data = data;
this.next = null;
this.prev = null;
}
}
class DoublyLinkedList {
Node head;
Node last;
boolean isEmpty() {
return head == null;
}
void displayForward() {
Node ptr = head;
System.out.print("[ ");
while (ptr != null) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.next;
}
System.out.println("]");
}
void displayBackward() {
Node ptr = last;
System.out.print("[ ");
while (ptr != null) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.prev;
}
System.out.println("]");
}
void insertFirst(int key, int data) {
Node link = new Node(key, data);
if (isEmpty()) {
last = link;
} else {
head.prev = link;
}
link.next = head;
head = link;
}
void insertLast(int key, int data) {
Node link = new Node(key, data);
if (isEmpty()) {
last = link;
} else {
last.next = link;
link.prev = last;
}
last = link;
}
Node deleteFirst() {
if (isEmpty()) {
return null;
}
Node tempLink = head;
if (head.next == null) {
last = null;
} else {
head.next.prev = null;
}
head = head.next;
return tempLink;
}
Node deleteLast() {
if (isEmpty()) {
return null;
}
Node tempLink = last;
if (head.next == null) {
head = null;
} else {
last.prev.next = null;
}
last = last.prev;
return tempLink;
}
Node delete(int key) {
Node current = head;
Node previous = null;
if (head == null) {
return null;
}
while (current.key != key) {
if (current.next == null) {
return null;
} else {
previous = current;
current = current.next;
}
}
if (current == head) {
head = head.next;
} else {
current.prev.next = current.next;
}
if (current == last) {
last = current.prev;
} else {
current.next.prev = current.prev;
}
return current;
}
boolean insertAfter(int key, int newKey, int data) {
Node current = head;
if (head == null) {
return false;
}
while (current.key != key) {
if (current.next == null) {
return false;
} else {
current = current.next;
}
}
Node newLink = new Node(newKey, data);
if (current == last) {
newLink.next = null;
last = newLink;
} else {
newLink.next = current.next;
current.next.prev = newLink;
}
newLink.prev = current;
current.next = newLink;
return true;
}
}
public class Main {
public static void main(String[] args) {
DoublyLinkedList dll = new DoublyLinkedList();
dll.insertFirst(1, 10);
dll.insertFirst(2, 20);
dll.insertFirst(3, 30);
dll.insertFirst(4, 1);
dll.insertFirst(5, 40);
dll.insertFirst(6, 56);
System.out.println("List (First to Last):");
dll.displayForward();
System.out.println();
System.out.println("List (Last to First):");
dll.displayBackward();
System.out.println("List, after deleting first record:");
dll.deleteFirst();
dll.displayForward();
System.out.println("List, after deleting last record:");
dll.deleteLast();
dll.displayForward();
System.out.println("List, insert after key(4):");
dll.insertAfter(4, 7, 13);
dll.displayForward();
System.out.println("List, after delete key(4):");
dll.delete(4);
dll.displayForward();
}
}
Output
List (First to Last):
[ (6, 56) (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ]
List (Last to First):
[ (1, 10) (2, 20) (3, 30) (4, 1) (5, 40) (6, 56) ]
List, after deleting first record:
[ (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ]
List, after deleting last record:
[ (5, 40) (4, 1) (3, 30) (2, 20) ]
List, insert after key(4):
[ (5, 40) (4, 1) (7, 13) (3, 30) (2, 20) ]
List, after delete key(4):
[ (5, 40) (7, 13) (3, 30) (2, 20) ]
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.next = None
self.prev = None
class DoublyLinkedList:
def __init__(self):
self.head = None
self.last = None
def is_empty(self):
return self.head is None
def display_forward(self):
ptr = self.head
print("[", end=" ")
while ptr:
print("({}, {})".format(ptr.key, ptr.data), end=" ")
ptr = ptr.next
print("]")
def display_backward(self):
ptr = self.last
print("[", end=" ")
while ptr:
print("({}, {})".format(ptr.key, ptr.data), end=" ")
ptr = ptr.prev
print("]")
def insert_first(self, key, data):
link = Node(key, data)
if self.is_empty():
self.last = link
else:
self.head.prev = link
link.next = self.head
self.head = link
def insert_last(self, key, data):
link = Node(key, data)
if self.is_empty():
self.last = link
else:
self.last.next = link
link.prev = self.last
self.last = link
def delete_first(self):
if self.is_empty():
return None
temp_link = self.head
if self.head.next is None:
self.last = None
else:
self.head.next.prev = None
self.head = self.head.next
return temp_link
def delete_last(self):
if self.is_empty():
return None
temp_link = self.last
if self.head.next is None:
self.head = None
else:
self.last.prev.next = None
self.last = self.last.prev
return temp_link
def delete(self, key):
current = self.head
while current and current.key != key:
current = current.next
if current is None:
return None
if current == self.head:
self.head = self.head.next
else:
current.prev.next = current.next
if current == self.last:
self.last = current.prev
else:
current.next.prev = current.prev
return current
def insert_after(self, key, new_key, data):
current = self.head
while current and current.key != key:
current = current.next
if current is None:
return False
new_link = Node(new_key, data)
if current == self.last:
new_link.next = None
self.last = new_link
else:
new_link.next = current.next
current.next.prev = new_link
new_link.prev = current
current.next = new_link
return True
# Example usage
dll = DoublyLinkedList()
dll.insert_first(1, 10)
dll.insert_first(2, 20)
dll.insert_first(3, 30)
dll.insert_first(4, 1)
dll.insert_first(5, 40)
dll.insert_first(6, 56)
print("List (First to Last):")
dll.display_forward()
print()
print("List (Last to First):")
dll.display_backward()
print("List, after deleting first record:")
dll.delete_first()
dll.display_forward()
print("List, after deleting last record:")
dll.delete_last()
dll.display_forward()
print("List, insert after key(4):")
dll.insert_after(4, 7, 13)
dll.display_forward()
print("List, after delete key(4):")
dll.delete(4)
dll.display_forward()
Output
List (First to Last):
[ (6, 56) (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ]
List (Last to First):
[ (1, 10) (2, 20) (3, 30) (4, 1) (5, 40) (6, 56) ]
List, after deleting first record:
[ (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ]
List, after deleting last record:
[ (5, 40) (4, 1) (3, 30) (2, 20) ]
List, insert after key(4):
[ (5, 40) (4, 1) (7, 13) (3, 30) (2, 20) ]
List, after delete key(4):
[ (5, 40) (7, 13) (3, 30) (2, 20) ]
Circular Linked List Data Structure
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the list in from first to last
void displayForward(){
//start from the beginning
struct node *ptr = head;
//navigate till the end of the list
printf("\n[ ");
while(ptr != NULL) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
printf(" ]");
}
//display the list from last to first
void displayBackward(){
//start from the last
struct node *ptr = last;
//navigate till the start of the list
printf("\n[ ");
while(ptr != NULL) {
//print data
printf("(%d,%d) ",ptr->key,ptr->data);
//move to next item
ptr = ptr ->prev;
printf(" ");
}
printf(" ]");
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//insert link at the last location
void insertLast(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL) {
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}
//delete link at the last location
struct node* deleteLast(){
//save reference to last link
struct node *tempLink = last;
//if only one link
if(head->next == NULL) {
head = NULL;
} else {
last->prev->next = NULL;
}
last = last->prev;
//return the deleted link
return tempLink;
}
//delete a link with given key
struct node* delete(int key){
//start from the first link
struct node* current = head;
struct node* previous = NULL;
//if list is empty
if(head == NULL) {
return NULL;
}
//navigate through list
while(current->key != key) {
//if it is last node
if(current->next == NULL) {
return NULL;
} else {
//store reference to current link
previous = current;
//move to next link
current = current->next;
}
}
//found a match, update the link
if(current == head) {
//change first to point to next link
head = head->next;
} else {
//bypass the current link
current->prev->next = current->next;
}
if(current == last) {
//change last to point to prev link
last = current->prev;
} else {
current->next->prev = current->prev;
}
return current;
}
bool insertAfter(int key, int newKey, int data){
//start from the first link
struct node *current = head;
//if list is empty
if(head == NULL) {
return false;
}
//navigate through list
while(current->key != key) {
//if it is last node
if(current->next == NULL) {
return false;
} else {
//move to next link
current = current->next;
}
}
//create a link
struct node *newLink = (struct node*) malloc(sizeof(struct node));
newLink->key = key;
newLink->data = data;
if(current == last) {
newLink->next = NULL;
last = newLink;
} else {
newLink->next = current->next;
current->next->prev = newLink;
}
newLink->prev = current;
current->next = newLink;
return true;
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nList (First to Last): ");
displayForward();
printf("\n");
printf("\nList (Last to first): ");
displayBackward();
printf("\nList , after deleting first record: ");
deleteFirst();
displayForward();
printf("\nList , after deleting last record: ");
deleteLast();
displayForward();
printf("\nList , insert after key(4) : ");
insertAfter(4,7, 13);
displayForward();
printf("\nList , after delete key(4) : ");
delete(4);
displayForward();
}
Output
List (First to Last): [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ] List (Last to first): [ (1,10) (2,20) (3,30) (4,1) (5,40) (6,56) ] List , after deleting first record: [ (5,40) (4,1) (3,30) (2,20) (1,10) ] List , after deleting last record: [ (5,40) (4,1) (3,30) (2,20) ] List , insert after key(4) : [ (5,40) (4,1) (4,13) (3,30) (2,20) ] List , after delete key(4) : [ (5,40) (4,13) (3,30) (2,20) ]
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
using namespace std;
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
//display the list in from first to last
void displayForward(){
//start from the beginning
struct node *ptr = head;
//navigate till the end of the list
cout << "\n[ ";
while(ptr != NULL) {
cout << "(" << ptr->key << "," << ptr->data << ")";
ptr = ptr->next;
}
cout << " ]" << endl;
}
//display the list from last to first
void displayBackward(){
//start from the last
struct node *ptr = last;
//navigate till the start of the list
cout << "\n[ ";
while(ptr != NULL) {
//print data
cout << "(" << ptr->key << "," << ptr->data << ")";
//move to next item
ptr = ptr ->prev;
cout << " ";
}
cout << " ]" << endl;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//insert link at the last location
void insertLast(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()) {
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL) {
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}
//delete link at the last location
struct node* deleteLast(){
//save reference to last link
struct node *tempLink = last;
//if only one link
if(head->next == NULL) {
head = NULL;
} else {
last->prev->next = NULL;
}
last = last->prev;
//return the deleted link
return tempLink;
}
//delete a link with given key
struct node* deletenode(int key){
//start from the first link
struct node* current = head;
struct node* previous = NULL;
//if list is empty
if(head == NULL) {
return NULL;
}
//navigate through list
while(current->key != key) {
//if it is last node
if(current->next == NULL) {
return NULL;
} else {
//store reference to current link
previous = current;
//move to next link
current = current->next;
}
}
//found a match, update the link
if(current == head) {
//change first to point to next link
head = head->next;
} else {
//bypass the current link
current->prev->next = current->next;
}
if(current == last) {
//change last to point to prev link
last = current->prev;
} else {
current->next->prev = current->prev;
}
return current;
}
bool insertAfter(int key, int newKey, int data){
//start from the first link
struct node *current = head;
//if list is empty
if(head == NULL) {
return false;
}
//navigate through list
while(current->key != key) {
//if it is last node
if(current->next == NULL) {
return false;
} else {
//move to next link
current = current->next;
}
}
//create a link
struct node *newLink = (struct node*) malloc(sizeof(struct node));
newLink->key = key;
newLink->data = data;
if(current == last) {
newLink->next = NULL;
last = newLink;
} else {
newLink->next = current->next;
current->next->prev = newLink;
}
newLink->prev = current;
current->next = newLink;
return true;
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nList (First to Last): ");
displayForward();
printf("\n");
printf("\nList (Last to first): ");
displayBackward();
printf("\nList , after deleting first record: ");
deleteFirst();
displayForward();
printf("\nList , after deleting last record: ");
deleteLast();
displayForward();
printf("\nList , insert after key(4) : ");
insertAfter(4, 7, 13);
displayForward();
printf("\nList , after delete key(4) : ");
deletenode(4);
displayForward();
return 0;
}
Output
List (First to Last): [ (6, 56) (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ] List (Last to First): [ (1, 10) (2, 20) (3, 30) (4, 1) (5, 40) (6, 56) ] List, after deleting first record: [ (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ] List, after deleting last record: [ (5, 40) (4, 1) (3, 30) (2, 20) ] List, insert after key(4): [ (5, 40) (4, 1) (7, 13) (3, 30) (2, 20) ] List, after delete key(4): [ (5, 40) (7, 13) (3, 30) (2, 20) ]
class Node {
int data;
int key;
Node next;
Node prev;
public Node(int key, int data) {
this.key = key;
this.data = data;
this.next = null;
this.prev = null;
}
}
class DoublyLinkedList {
Node head;
Node last;
boolean isEmpty() {
return head == null;
}
void displayForward() {
Node ptr = head;
System.out.print("[ ");
while (ptr != null) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.next;
}
System.out.println("]");
}
void displayBackward() {
Node ptr = last;
System.out.print("[ ");
while (ptr != null) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.prev;
}
System.out.println("]");
}
void insertFirst(int key, int data) {
Node link = new Node(key, data);
if (isEmpty()) {
last = link;
} else {
head.prev = link;
}
link.next = head;
head = link;
}
void insertLast(int key, int data) {
Node link = new Node(key, data);
if (isEmpty()) {
last = link;
} else {
last.next = link;
link.prev = last;
}
last = link;
}
Node deleteFirst() {
if (isEmpty()) {
return null;
}
Node tempLink = head;
if (head.next == null) {
last = null;
} else {
head.next.prev = null;
}
head = head.next;
return tempLink;
}
Node deleteLast() {
if (isEmpty()) {
return null;
}
Node tempLink = last;
if (head.next == null) {
head = null;
} else {
last.prev.next = null;
}
last = last.prev;
return tempLink;
}
Node delete(int key) {
Node current = head;
Node previous = null;
if (head == null) {
return null;
}
while (current.key != key) {
if (current.next == null) {
return null;
} else {
previous = current;
current = current.next;
}
}
if (current == head) {
head = head.next;
} else {
current.prev.next = current.next;
}
if (current == last) {
last = current.prev;
} else {
current.next.prev = current.prev;
}
return current;
}
boolean insertAfter(int key, int newKey, int data) {
Node current = head;
if (head == null) {
return false;
}
while (current.key != key) {
if (current.next == null) {
return false;
} else {
current = current.next;
}
}
Node newLink = new Node(newKey, data);
if (current == last) {
newLink.next = null;
last = newLink;
} else {
newLink.next = current.next;
current.next.prev = newLink;
}
newLink.prev = current;
current.next = newLink;
return true;
}
}
public class Main {
public static void main(String[] args) {
DoublyLinkedList dll = new DoublyLinkedList();
dll.insertFirst(1, 10);
dll.insertFirst(2, 20);
dll.insertFirst(3, 30);
dll.insertFirst(4, 1);
dll.insertFirst(5, 40);
dll.insertFirst(6, 56);
System.out.println("List (First to Last):");
dll.displayForward();
System.out.println();
System.out.println("List (Last to First):");
dll.displayBackward();
System.out.println("List, after deleting first record:");
dll.deleteFirst();
dll.displayForward();
System.out.println("List, after deleting last record:");
dll.deleteLast();
dll.displayForward();
System.out.println("List, insert after key(4):");
dll.insertAfter(4, 7, 13);
dll.displayForward();
System.out.println("List, after delete key(4):");
dll.delete(4);
dll.displayForward();
}
}
Output
List (First to Last): [ (6, 56) (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ] List (Last to First): [ (1, 10) (2, 20) (3, 30) (4, 1) (5, 40) (6, 56) ] List, after deleting first record: [ (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ] List, after deleting last record: [ (5, 40) (4, 1) (3, 30) (2, 20) ] List, insert after key(4): [ (5, 40) (4, 1) (7, 13) (3, 30) (2, 20) ] List, after delete key(4): [ (5, 40) (7, 13) (3, 30) (2, 20) ]
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.next = None
self.prev = None
class DoublyLinkedList:
def __init__(self):
self.head = None
self.last = None
def is_empty(self):
return self.head is None
def display_forward(self):
ptr = self.head
print("[", end=" ")
while ptr:
print("({}, {})".format(ptr.key, ptr.data), end=" ")
ptr = ptr.next
print("]")
def display_backward(self):
ptr = self.last
print("[", end=" ")
while ptr:
print("({}, {})".format(ptr.key, ptr.data), end=" ")
ptr = ptr.prev
print("]")
def insert_first(self, key, data):
link = Node(key, data)
if self.is_empty():
self.last = link
else:
self.head.prev = link
link.next = self.head
self.head = link
def insert_last(self, key, data):
link = Node(key, data)
if self.is_empty():
self.last = link
else:
self.last.next = link
link.prev = self.last
self.last = link
def delete_first(self):
if self.is_empty():
return None
temp_link = self.head
if self.head.next is None:
self.last = None
else:
self.head.next.prev = None
self.head = self.head.next
return temp_link
def delete_last(self):
if self.is_empty():
return None
temp_link = self.last
if self.head.next is None:
self.head = None
else:
self.last.prev.next = None
self.last = self.last.prev
return temp_link
def delete(self, key):
current = self.head
while current and current.key != key:
current = current.next
if current is None:
return None
if current == self.head:
self.head = self.head.next
else:
current.prev.next = current.next
if current == self.last:
self.last = current.prev
else:
current.next.prev = current.prev
return current
def insert_after(self, key, new_key, data):
current = self.head
while current and current.key != key:
current = current.next
if current is None:
return False
new_link = Node(new_key, data)
if current == self.last:
new_link.next = None
self.last = new_link
else:
new_link.next = current.next
current.next.prev = new_link
new_link.prev = current
current.next = new_link
return True
# Example usage
dll = DoublyLinkedList()
dll.insert_first(1, 10)
dll.insert_first(2, 20)
dll.insert_first(3, 30)
dll.insert_first(4, 1)
dll.insert_first(5, 40)
dll.insert_first(6, 56)
print("List (First to Last):")
dll.display_forward()
print()
print("List (Last to First):")
dll.display_backward()
print("List, after deleting first record:")
dll.delete_first()
dll.display_forward()
print("List, after deleting last record:")
dll.delete_last()
dll.display_forward()
print("List, insert after key(4):")
dll.insert_after(4, 7, 13)
dll.display_forward()
print("List, after delete key(4):")
dll.delete(4)
dll.display_forward()
Output
List (First to Last): [ (6, 56) (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ] List (Last to First): [ (1, 10) (2, 20) (3, 30) (4, 1) (5, 40) (6, 56) ] List, after deleting first record: [ (5, 40) (4, 1) (3, 30) (2, 20) (1, 10) ] List, after deleting last record: [ (5, 40) (4, 1) (3, 30) (2, 20) ] List, insert after key(4): [ (5, 40) (4, 1) (7, 13) (3, 30) (2, 20) ] List, after delete key(4): [ (5, 40) (7, 13) (3, 30) (2, 20) ]
Circular Linked List is a variation of Linked list in which the first element points to the last element and the last element points to the first element. Both Singly Linked List and Doubly Linked List can be made into a circular linked list.
Singly Linked List as Circular
In singly linked list, the next pointer of the last node points to the first node.

Doubly Linked List as Circular
In doubly linked list, the next pointer of the last node points to the first node and the previous pointer of the first node points to the last node making the circular in both directions.

As per the above illustration, following are the important points to be considered.
The last link's next points to the first link of the list in both cases of singly as well as doubly linked list.
The first link's previous points to the last of the list in case of doubly linked list.
Basic Operations
Following are the important operations supported by a circular list.
insert − Inserts an element at the start of the list.
delete − Deletes an element from the start of the list.
display − Displays the list.
Insertion Operation
The insertion operation of a circular linked list only inserts the element at the start of the list. This differs from the usual singly and doubly linked lists as there is no particular starting and ending points in this list. The insertion is done either at the start or after a particular node (or a given position) in the list.
Algorithm
1. START 2. Check if the list is empty 3. If the list is empty, add the node and point the head to this node 4. If the list is not empty, link the existing head as the next node to the new node. 5. Make the new node as the new head. 6. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
void main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Circular Linked List: ");
//print list
printList();
}
Output
Circular Linked List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ]
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Circular Linked List: ");
//print list
printList();
return 0;
}
Output
Circular Linked List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ]
//Java program for circular link list
import java.util.*;
class Node {
int data;
int key;
Node next;
}
public class Main {
static Node head = null;
static Node current = null;
static boolean isEmpty() {
return head == null;
}
//insert link at the first location
static void insertFirst(int key, int data) {
//create a link
Node link = new Node();
link.key = key;
link.data = data;
if (isEmpty()) {
head = link;
head.next = head;
} else {
//point it to old first node
link.next = head;
//point first to new first node
head = link;
}
}
//display the list
static void printList() {
Node ptr = head;
System.out.print("\n[ ");
//start from the beginning
if (head != null) {
while (ptr.next != ptr) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.next;
}
}
System.out.print(" ]");
}
public static void main(String[] args) {
insertFirst(1, 10);
insertFirst(2, 20);
insertFirst(3, 30);
insertFirst(4, 1);
insertFirst(5, 40);
insertFirst(6, 56);
System.out.print("Circular Linked List: ");
//print list
printList();
}
}
Output
Circular Linked List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ]
#python program for circular linked list
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.next = None
head = None
current = None
def is_empty():
return head is None
#insert link at the first location
def insert_first(key, data):
#create a link
global head
new_node = Node(key, data)
if is_empty():
head = new_node
head.next = head
else:
#point it to old first node
new_node.next = head
#point first to the new first node
head = new_node
#display the list
def print_list():
global head
ptr = head
print("[", end=" ")
#start from the beginning
if head is not None:
while ptr.next != ptr:
print("({}, {})".format(ptr.key, ptr.data), end=" ")
ptr = ptr.next
print("]")
insert_first(1, 10)
insert_first(2, 20)
insert_first(3, 30)
insert_first(4, 1)
insert_first(5, 40)
insert_first(6, 56)
#printlist
print("Circular Linked List: ")
print_list()
Output
Circular Linked List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ]
Deletion Operation
The Deletion operation in a Circular linked list removes a certain node from the list. The deletion operation in this type of lists can be done at the beginning, or a given position, or at the ending.
Algorithm
1. START 2. If the list is empty, then the program is returned. 3. If the list is not empty, we traverse the list using a current pointer that is set to the head pointer and create another pointer previous that points to the last node. 4. Suppose the list has only one node, the node is deleted by setting the head pointer to NULL. 5. If the list has more than one node and the first node is to be deleted, the head is set to the next node and the previous is linked to the new head. 6. If the node to be deleted is the last node, link the preceding node of the last node to head node. 7. If the node is neither first nor last, remove the node by linking its preceding node to its succeeding node. 8. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//delete first item
struct node * deleteFirst(){
//save reference to first link
struct node *tempLink = head;
if(head->next == head) {
head = NULL;
return tempLink;
}
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
//display the list
void printList(){
struct node *ptr = head;
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
}
void main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Circular Linked List: ");
//print list
printList();
deleteFirst();
printf("\nList after deleting the first item: ");
printList();
}
Output
Circular Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) List after deleting the first item: (5,40) (4,1) (3,30) (2,20)
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//delete first item
struct node * deleteFirst(){
//save reference to first link
struct node *tempLink = head;
if(head->next == head) {
head = NULL;
return tempLink;
}
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
//display the list
void printList(){
struct node *ptr = head;
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Circular Linked List: ");
//print list
printList();
deleteFirst();
printf("\nList after deleting the first item: ");
printList();
return 0;
}
Output
Circular Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) List after deleting the first item: (5,40) (4,1) (3,30) (2,20)
//Java program for circular linked list
import java.util.*;
public class Main {
static class Node {
int data;
int key;
Node next;
}
static Node head = null;
static Node current = null;
static boolean isEmpty() {
return head == null;
}
//insert link at the first location
static void insertFirst(int key, int data) {
//create a link
Node link = new Node();
link.key = key;
link.data = data;
if (isEmpty()) {
head = link;
head.next = head;
} else {
//point it to old first node
link.next = head;
//point first to new first node
head = link;
}
}
//delete first item
static Node deleteFirst() {
//save reference to first link
Node tempLink = head;
if (head.next == head) {
head = null;
return tempLink;
}
//mark next to first link as first
head = head.next;
//return the deleted link
return tempLink;
}
//display the list
static void printList() {
Node ptr = head;
//start from the beginning
if (head != null) {
while (ptr.next != ptr) {
System.out.printf("(%d,%d) ", ptr.key, ptr.data);
ptr = ptr.next;
}
}
}
public static void main(String[] args) {
insertFirst(1, 10);
insertFirst(2, 20);
insertFirst(3, 30);
insertFirst(4, 1);
insertFirst(5, 40);
insertFirst(6, 56);
System.out.print("Circular Linked List: ");
//print list
printList();
deleteFirst();
}
}
Output
Circular Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) List after deleting the first item: (5,40) (4,1) (3,30) (2,20)
#python program for circular linked list
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.next = None
head = None
current = None
def is_empty():
return head is None
#insert link at the first location
def insert_first(key, data):
#create a link
global head
new_node = Node(key, data)
if is_empty():
head = new_node
head.next = head
else:
#point it to old first node
new_node.next = head
#point first to the new first node
head = new_node
def print_list():
global head
ptr = head
print("[", end=" ")
#start from the beginning
if head is not None:
while ptr.next != ptr:
print("({}, {})".format(ptr.key, ptr.data), end=" ")
ptr = ptr.next
print("]")
def delete_first():
global head
temp_link = head
if head.next == head:
head = None
return temp_link
head = head.next
return temp_link
insert_first(1, 10)
insert_first(2, 20)
insert_first(3, 30)
insert_first(4, 1)
insert_first(5, 40)
insert_first(6, 56)
#printlist
print("Circular Linked List: ")
print_list()
delete_first()
print("\nList after deleting the first item: ")
print_list();
Output
Circular Linked List: (6,56) (5,40) (4,1) (3,30) (2,20) List after deleting the first item: (5,40) (4,1) (3,30) (2,20)
Display List Operation
The Display List operation visits every node in the list and prints them all in the output.
Algorithm
1. START 2. Walk through all the nodes of the list and print them 3. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
void main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Circular Linked List: ");
//print list
printList();
}
Output
Circular Linked List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ]
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Circular Linked List: ");
//print list
printList();
return 0;
}
Output
Circular Linked List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ]
//Java program for circular link list
import java.util.*;
class Node {
int data;
int key;
Node next;
}
public class Main {
static Node head = null;
static Node current = null;
static boolean isEmpty() {
return head == null;
}
//insert link at the first location
static void insertFirst(int key, int data) {
//create a link
Node link = new Node();
link.key = key;
link.data = data;
if (isEmpty()) {
head = link;
head.next = head;
} else {
//point it to old first node
link.next = head;
//point first to new first node
head = link;
}
}
//display the list
static void printList() {
Node ptr = head;
System.out.print("\n[ ");
//start from the beginning
if (head != null) {
while (ptr.next != ptr) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.next;
}
}
System.out.print(" ]");
}
public static void main(String[] args) {
insertFirst(1, 10);
insertFirst(2, 20);
insertFirst(3, 30);
insertFirst(4, 1);
insertFirst(5, 40);
insertFirst(6, 56);
System.out.print("Circular Linked List: ");
//print list
printList();
}
}
Output
Circular Linked List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ]
#python program for circular linked list
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.next = None
head = None
current = None
def is_empty():
return head is None
#insert link at the first location
def insert_first(key, data):
#create a link
global head
new_node = Node(key, data)
if is_empty():
head = new_node
head.next = head
else:
#point it to old first node
new_node.next = head
#point first to the new first node
head = new_node
#display the list
def print_list():
global head
ptr = head
print("[", end=" ")
#start from the beginning
if head is not None:
while ptr.next != ptr:
print("({}, {})".format(ptr.key, ptr.data), end=" ")
ptr = ptr.next
print("]")
insert_first(1, 10)
insert_first(2, 20)
insert_first(3, 30)
insert_first(4, 1)
insert_first(5, 40)
insert_first(6, 56)
#printlist
print("Circular Linked List: ")
print_list()
Output
Circular Linked List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ]
Complete implementation
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
int length(){
int length = 0;
//if list is empty
if(head == NULL) {
return 0;
}
current = head->next;
while(current != head) {
length++;
current = current->next;
}
return length;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//delete first item
struct node * deleteFirst(){
//save reference to first link
struct node *tempLink = head;
if(head->next == head) {
head = NULL;
return tempLink;
}
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Original List: ");
//print list
printList();
while(!isEmpty()) {
struct node *temp = deleteFirst();
printf("\nDeleted value:");
printf("(%d,%d) ",temp->key,temp->data);
}
printf("\nList after deleting all items: ");
printList();
}
Output
Original List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ] Deleted value:(6,56) Deleted value:(5,40) Deleted value:(4,1) Deleted value:(3,30) Deleted value:(2,20) Deleted value:(1,10) List after deleting all items: [ ]
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdbool>
using namespace std;
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
int length(){
int length = 0;
//if list is empty
if(head == NULL) {
return 0;
}
current = head->next;
while(current != head) {
length++;
current = current->next;
}
return length;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//delete first item
struct node * deleteFirst(){
//save reference to first link
struct node *tempLink = head;
if(head->next == head) {
head = NULL;
return tempLink;
}
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
//display the list
void printList(){
struct node *ptr = head;
cout << "\n[ ";
//start from the beginning
if(head != NULL) {
while(ptr->next != ptr) {
cout << "(" << ptr->key << "," << ptr->data << ") ";
ptr = ptr->next;
}
}
cout << " ]";
}
int main(){
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
cout << "Original List: ";
//print list
printList();
while(!isEmpty()) {
struct node *temp = deleteFirst();
cout << "\n Deleted value:";
cout << "(" << temp->key << "," << temp->data << ") ";
}
cout << "\n List after deleting all items: ";
printList();
return 0;
}
Output
Original List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ] Deleted value:(6,56) Deleted value:(5,40) Deleted value:(4,1) Deleted value:(3,30) Deleted value:(2,20) Deleted value:(1,10) List after deleting all items: [ ]
class Node {
int data;
int key;
Node next;
Node(int key, int data) {
this.key = key;
this.data = data;
this.next = null;
}
}
public class LinkedList {
private Node head;
private Node current;
boolean isEmpty() {
return head == null;
}
int length() {
int length = 0;
//if list is empty
if (head == null) {
return 0;
}
current = head.next;
while (current != head) {
length++;
current = current.next;
}
return length;
}
//insert link at the first location
void insertFirst(int key, int data) {
//create a link
Node link = new Node(key, data);
if (isEmpty()) {
head = link;
head.next = head;
} else {
//point it to old first node
link.next = head;
//point first to new first node
head = link;
}
}
//delete first item
Node deleteFirst() {
if (head.next == head) {
//save reference to first link
Node tempLink = head;
head = null;
return tempLink;
}
Node tempLink = head;
//mark next to first link as first
head = head.next;
//return the deleted link
return tempLink;
}
//display the list
void printList() {
Node ptr = head;
System.out.print("\n[ ");
//start from the beginning
if (head != null) {
while (ptr.next != ptr) {
System.out.print("(" + ptr.key + "," + ptr.data + ") ");
ptr = ptr.next;
}
}
System.out.print(" ]");
}
public static void main(String[] args) {
LinkedList linkedList = new LinkedList();
linkedList.insertFirst(1, 10);
linkedList.insertFirst(2, 20);
linkedList.insertFirst(3, 30);
linkedList.insertFirst(4, 1);
linkedList.insertFirst(5, 40);
linkedList.insertFirst(6, 56);
System.out.print("Original List: ");
linkedList.printList();
//print list
while (!linkedList.isEmpty()) {
Node temp = linkedList.deleteFirst();
System.out.println("\nDeleted value: (" + temp.key + "," + temp.data + ")");
}
System.out.print("\nList after deleting all items: ");
linkedList.printList();
}
}
Output
Original List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ] Deleted value: (6,56) Deleted value: (5,40) Deleted value: (4,1) Deleted value: (3,30) Deleted value: (2,20) Deleted value: (1,10) List after deleting all items: [ ]
class Node:
def __init__(self, key, data):
self.key = key
self.data = data
self.next = None
class LinkedList:
def __init__(self):
self.head = None
self.current = None
def is_empty(self):
return self.head is None
def length(self):
length = 0
# If list is empty
if self.head is None:
return 0
self.current = self.head.next
while self.current != self.head:
length += 1
self.current = self.current.next
return length
# insert link at the first location
def insert_first(self, key, data):
# create a link
new_node = Node(key, data)
if self.is_empty():
self.head = new_node
self.head.next = self.head
else:
# point it to old first node
new_node.next = self.head
# point first to new first node
self.head = new_node
# delete first item
def delete_first(self):
# save reference to first link
if self.head.next == self.head:
temp_link = self.head
self.head = None
return temp_link
# mark next to first link as first
temp_link = self.head
self.head = self.head.next
# return the deleted link
return temp_link
# Diplay the list
def print_list(self):
ptr = self.head
print("[", end=" ")
# start from the beginning
if self.head is not None:
while ptr.next != ptr:
print("({}, {})".format(ptr.key, ptr.data), end=" ")
ptr = ptr.next
print("]")
# Main function
if __name__ == '__main__':
linked_list = LinkedList()
linked_list.insert_first(1, 10)
linked_list.insert_first(2, 20)
linked_list.insert_first(3, 30)
linked_list.insert_first(4, 1)
linked_list.insert_first(5, 40)
linked_list.insert_first(6, 56)
print("Original List: ", end="")
linked_list.print_list()
while not linked_list.is_empty():
temp = linked_list.delete_first()
print("\nDeleted value: ({}, {})".format(temp.key, temp.data))
# print list
print("List after deleting all items: ", end="")
linked_list.print_list()
Output
Original List: [ (6, 56) (5, 40) (4, 1) (3, 30) (2, 20) ] Deleted value: (6, 56) Deleted value: (5, 40) Deleted value: (4, 1) Deleted value: (3, 30) Deleted value: (2, 20)Deleted value: (1, 10) List after deleting all items: [ ]
Stack Data Structure
A stack is an Abstract Data Type (ADT), that is popularly used in most programming languages. It is named stack because it has the similar operations as the real-world stacks, for example a pack of cards or a pile of plates, etc.

The stack follows the LIFO (Last in - First out) structure where the last element inserted would be the first element deleted.
Stack Representation
A Stack ADT allows all data operations at one end only. At any given time, we can only access the top element of a stack.
The following diagram depicts a stack and its operations −
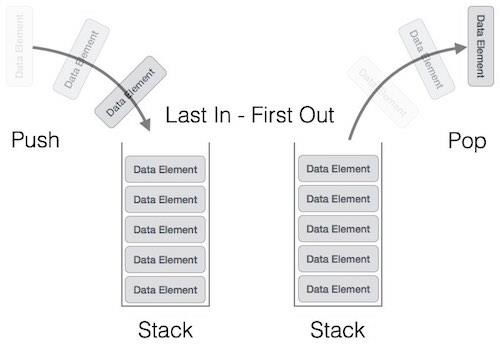
A stack can be implemented by means of Array, Structure, Pointer, and Linked List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays, which makes it a fixed size stack implementation.
Basic Operations on Stacks
Stack operations usually are performed for initialization, usage and, de-initialization of the stack ADT.
The most fundamental operations in the stack ADT include: push(), pop(), peek(), isFull(), isEmpty(). These are all built-in operations to carry out data manipulation and to check the status of the stack.
Stack uses pointers that always point to the topmost element within the stack, hence called as the top pointer.
Insertion: push()
push() is an operation that inserts elements into the stack. The following is an algorithm that describes the push() operation in a simpler way.
Algorithm
1 Checks if the stack is full. 2 If the stack is full, produces an error and exit. 3 If the stack is not full, increments top to point next empty space. 4 Adds data element to the stack location, where top is pointing. 5 Returns success.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full*/
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full*/
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0
import java.io.*;
import java.util.*; // util imports the stack class
public class StackExample {
public static void main (String[] args) {
Stack<Integer> stk = new Stack<Integer>();
// inserting elements into the stack
stk.push(52);
stk.push(19);
stk.push(33);
stk.push(14);
stk.push(6);
System.out.print("The stack is: " + stk);
}
}
Output
The stack is: [52, 19, 33, 14, 6]
class Stack:
def __init__(self):
self.stack = []
def __str__(self):
return str(self.stack)
def push(self, data):
if data not in self.stack:
self.stack.append(data)
return True
else:
return False
stk = Stack()
stk.push(1)
stk.push(2)
stk.push(3)
stk.push(4)
stk.push(5)
print("Stack Elements:")
print(stk)
Output
Stack Elements: [1, 2, 3, 4, 5]
Note − In Java we have used to built-in method push() to perform this operation.
Deletion: pop()
pop() is a data manipulation operation which removes elements from the stack. The following pseudo code describes the pop() operation in a simpler way.
Algorithm
1 Checks if the stack is empty. 2 If the stack is empty, produces an error and exit. 3 If the stack is not empty, accesses the data element at which top is pointing. 4 Decreases the value of top by 1. 5 Returns success.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full*/
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to delete from the stack */
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
/*printf("Element at top of the stack: %d\n" ,peek());*/
printf("\nElements popped: \n");
// print stack data
while(!isempty()) {
int data = pop();
printf("%d ",data);
}
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Elements popped: 15 123 62 10 44
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full*/
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to delete from the stack */
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
/*printf("Element at top of the stack: %d\n" ,peek());*/
printf("\nElements popped: \n");
// print stack data
while(!isempty()) {
int data = pop();
printf("%d ",data);
}
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Elements popped: 15 123 62 10 44
import java.io.*;
import java.util.*;
// util imports the stack class
public class StackExample {
public static void main (String[] args) {
Stack<Integer> stk = new Stack<Integer>();
// Inserting elements into the stack
stk.push(52);
stk.push(19);
stk.push(33);
stk.push(14);
stk.push(6);
System.out.print("The stack is: " + stk);
// Deletion from the stack
System.out.print("\nThe popped element is: ");
Integer n = (Integer) stk.pop();
System.out.print(n);
}
}
Output
The stack is: [52, 19, 33, 14, 6] The popped element is: 6
class Stack:
def __init__(self):
self.stack = []
def __str__(self):
return str(self.stack)
def push(self, data):
if data not in self.stack:
self.stack.append(data)
return True
else:
return False
def remove(self):
if len(self.stack) <= 0:
return ("No element in the Stack")
else:
return self.stack.pop()
stk = Stack()
stk.push(1)
stk.push(2)
stk.push(3)
stk.push(4)
stk.push(5)
print("Stack Elements:")
print(stk)
print("----Deletion operation in stack----")
p = stk.remove()
print("The popped element is: " + str(p))
print("Updated Stack:")
print(stk)
Output
Stack Elements: [1, 2, 3, 4, 5] ----Deletion operation in stack---- The popped element is: 5 Updated Stack: [1, 2, 3, 4]
Note − In Java we are using the built-in method pop().
peek()
The peek() is an operation retrieves the topmost element within the stack, without deleting it. This operation is used to check the status of the stack with the help of the top pointer.
Algorithm
1. START 2. return the element at the top of the stack 3. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
int peek(){
return stack[top];
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
printf("\nElement at top of the stack: %d\n" ,peek());
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Element at top of the stack: 15
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
int peek(){
return stack[top];
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
int i;
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Stack Elements: \n");
// print stack data
for(i = 0; i < 8; i++) {
printf("%d ", stack[i]);
}
printf("\nElement at top of the stack: %d\n" ,peek());
return 0;
}
Output
Stack Elements: 44 10 62 123 15 0 0 0 Element at top of the stack: 15
import java.io.*;
import java.util.*;
// util imports the stack class
public class StackExample {
public static void main (String[] args) {
Stack<Integer> stk = new Stack<Integer>();
// inserting elements into the stack
stk.push(52);
stk.push(19);
stk.push(33);
stk.push(14);
stk.push(6);
System.out.print("The stack is: " + stk);
Integer pos = (Integer) stk.peek();
System.out.print("\nThe element found is " + pos);
}
}
Output
The stack is: [52, 19, 33, 14, 6] The element found is 6
class Stack:
def __init__(self):
self.stack = []
def __str__(self):
return str(self.stack)
def push(self, data):
if data not in self.stack:
self.stack.append(data)
return True
else:
return False
# Use peek to look at the top of the stack
def peek(self):
return self.stack[-1]
stk = Stack()
stk.push(1)
stk.push(2)
stk.push(3)
stk.push(4)
stk.push(5)
print("Stack Elements:")
print(stk)
print("topmost element: ",stk.peek())
Output
Stack Elements: [1, 2, 3, 4, 5] topmost element: 5
isFull()
isFull() operation checks whether the stack is full. This operation is used to check the status of the stack with the help of top pointer.
Algorithm
1. START 2. If the size of the stack is equal to the top position of the stack, the stack is full. Return 1. 3. Otherwise, return 0. 4. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Main function */
int main(){
printf("Stack full: %s\n" , isfull()?"true":"false");
return 0;
}
Output
Stack full: false
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Main function */
int main(){
printf("Stack full: %s\n" , isfull()?"true":"false");
return 0;
}
Output
Stack full: false
import java.io.*;
public class StackExample {
private int arr[];
private int top;
private int capacity;
StackExample(int size) {
arr = new int[size];
capacity = size;
top = -1;
}
public boolean isEmpty() {
return top == -1;
}
public boolean isFull() {
return top == capacity - 1;
}
public void push(int key) {
if (isFull()) {
System.out.println("Stack is Full\n");
return;
}
arr[++top] = key;
}
public static void main (String[] args) {
StackExample stk = new StackExample(5);
stk.push(1); // inserting 1 in the stack
stk.push(2);
stk.push(3);
stk.push(4);
stk.push(5);
System.out.println("Stack Full? " + stk.isFull());
}
}
Output
Stack Full? true
#python code for stack(IsFull)
MAXSIZE = 8
stack = [None] * MAXSIZE
top = -1
#Check if the stack is empty
def isfull():
if top == MAXSIZE - 1:
return True
else:
return False
#main function
print("Stack full:", isfull())
Output
Stack full: False
isEmpty()
The isEmpty() operation verifies whether the stack is empty. This operation is used to check the status of the stack with the help of top pointer.
Algorithm
1. START 2. If the top value is -1, the stack is empty. Return 1. 3. Otherwise, return 0. 4. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty() {
if(top == -1)
return 1;
else
return 0;
}
/* Main function */
int main() {
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
Output
Stack empty: true
#include <iostream>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Main function */
int main(){
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
Output
Stack empty: true
import java.io.*;
import java.util.*; // util imports the stack class
public class StackExample {
public static void main (String[] args) {
Stack<Integer> stk = new Stack<Integer>();
// Inserting elements into the stack
stk.push(52);
stk.push(19);
stk.push(33);
stk.push(14);
stk.push(6);
System.out.println("Stack empty? "+ stk.isEmpty());
}
}
Output
Stack empty? false
#python code for stack(IsFull)
MAXSIZE = 8
stack = [None] * MAXSIZE
top = -1
#Check if the stack is empty
def isempty():
if top == -1:
return True
else:
return False
#main function
print("Stack empty:", isempty())
Output
Stack empty: True
Complete implementation
#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
int peek(){
return stack[top];
}
/* Function to delete from the stack */
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data, Stack is empty.\n");
}
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data, Stack is full.\n");
}
}
/* Main function */
int main(){
push(44);
push(10);
push(62);
push(123);
push(15);
printf("Element at top of the stack: %d\n" ,peek());
printf("Elements: \n");
// print stack data
while(!isempty()) {
int data = pop();
printf("%d\n",data);
}
printf("Stack full: %s\n" , isfull()?"true":"false");
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
Output
Element at top of the stack: 15 Elements: 15123 62 10 44 Stack full: false Stack empty: true
#include <iostream>
using namespace std;
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the topmost element in the stack */
int peek(){
return stack[top];
}
/* Function to delete from the stack */
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else
cout << "Could not retrieve data, Stack is empty." << endl;
}
/* Function to insert into the stack */
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else
cout << "Could not insert data, Stack is full." << endl;
}
/* Main function */
int main(){
push(44);
push(10);
push(62);
push(123);
push(15);
cout << "Element at top of the stack: " << peek() << endl;
printf("Elements: \n");
// print stack data
while(!isempty()) {
int data = pop();
cout << data <<endl;
}
printf("Stack full: %s\n" , isfull()?"true":"false");
printf("Stack empty: %s\n" , isempty()?"true":"false");
return 0;
}
Output
Element at top of the stack: 15 Elements: 15 123 62 10 44 Stack full: false Stack empty: true
import java.io.*;
import java.util.*; // util imports the stack class
public class StackExample {
public static void main (String[] args) {
Stack<Integer> stk = new Stack<Integer>();
// inserting elements into the stack
stk.push(52);
stk.push(19);
stk.push(33);
stk.push(14);
stk.push(6);
System.out.print("The stack is: " + stk);
// deletion from the stack
System.out.print("\nThe popped element is: ");
Integer n = (Integer) stk.pop();
System.out.print(n);
// searching for an element in the stack
Integer pos = (Integer) stk.search(19);
if(pos == -1)
System.out.print("\nThe element 19 not found in stack");
else
System.out.print("\nThe element 19 is found at " + pos);
}
}
Output
The stack is: [52, 19, 33, 14, 6] The popped element is: 6 The element 19 is found at 3
class Stack:
def __init__(self):
self.stack = []
def add(self, data):
if data not in self.stack:
self.stack.append(data)
return True
else:
return False
# Use peek to look at the top of the stack
def peek(self):
return self.stack[-1]
# Use list pop method to remove element
def remove(self):
if len(self.stack) <= 0:
return ("No element in the Stack")
else:
return self.stack.pop()
stk = Stack()
stk.add(1)
stk.add(2)
stk.add(3)
stk.add(4)
stk.add(5)
print("topmost element: ",stk.peek())
print("----Deletion operation in stack----")
stk.remove()
stk.peek()
print("topmost element after deletion: ",stk.peek())
Output
topmost element: 5 ----Deletion operation in stack---- topmost element after deletion: 4
Expression Parsing
The way to write arithmetic expression is known as a notation. An arithmetic expression can be written in three different but equivalent notations, i.e., without changing the essence or output of an expression. These notations are −
- Infix Notation
- Prefix (Polish) Notation
- Postfix (Reverse-Polish) Notation
These notations are named as how they use operator in expression. We shall learn the same here in this chapter.
Infix Notation
We write expression in infix notation, e.g. a - b + c, where operators are used in-between operands. It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices. An algorithm to process infix notation could be difficult and costly in terms of time and space consumption.
Prefix Notation
In this notation, operator is prefixed to operands, i.e. operator is written ahead of operands. For example, +ab. This is equivalent to its infix notation a + b. Prefix notation is also known as Polish Notation.
Postfix Notation
This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands i.e., the operator is written after the operands. For example, ab+. This is equivalent to its infix notation a + b.
The following table briefly tries to show the difference in all three notations −
| Sr.No. | Infix Notation | Prefix Notation | Postfix Notation |
|---|---|---|---|
| 1 | a + b | + a b | a b + |
| 2 | (a + b) ∗ c | ∗ + a b c | a b + c ∗ |
| 3 | a ∗ (b + c) | ∗ a + b c | a b c + ∗ |
| 4 | a / b + c / d | + / a b / c d | a b / c d / + |
| 5 | (a + b) ∗ (c + d) | ∗ + a b + c d | a b + c d + ∗ |
| 6 | ((a + b) ∗ c) - d | - ∗ + a b c d | a b + c ∗ d - |
Parsing Expressions
As we have discussed, it is not a very efficient way to design an algorithm or program to parse infix notations. Instead, these infix notations are first converted into either postfix or prefix notations and then computed.
To parse any arithmetic expression, we need to take care of operator precedence and associativity also.
Precedence
When an operand is in between two different operators, which operator will take the operand first, is decided by the precedence of an operator over others. For example −

As multiplication operation has precedence over addition, b * c will be evaluated first. A table of operator precedence is provided later.
Associativity
Associativity describes the rule where operators with the same precedence appear in an expression. For example, in expression a + b c, both + and have the same precedence, then which part of the expression will be evaluated first, is determined by associativity of those operators. Here, both + and are left associative, so the expression will be evaluated as (a + b) c.
Precedence and associativity determines the order of evaluation of an expression. Following is an operator precedence and associativity table (highest to lowest) −
| Sr.No. | Operator | Precedence | Associativity |
|---|---|---|---|
| 1 | Exponentiation ^ | Highest | Right Associative |
| 2 | Multiplication ( ∗ ) & Division ( / ) | Second Highest | Left Associative |
| 3 | Addition ( + ) & Subtraction ( − ) | Lowest | Left Associative |
The above table shows the default behavior of operators. At any point of time in expression evaluation, the order can be altered by using parenthesis. For example −
In a + b*c, the expression part b*c will be evaluated first, with multiplication as precedence over addition. We here use parenthesis for a + b to be evaluated first, like (a + b)*c.
Postfix Evaluation Algorithm
We shall now look at the algorithm on how to evaluate postfix notation −
Step 1 scan the expression from left to right Step 2 if it is an operand push it to stack Step 3 if it is an operator pull operand from stack and perform operation Step 4 store the output of step 3, back to stack Step 5 scan the expression until all operands are consumed Step 6 pop the stack and perform operation
Complete implementation
#include<stdio.h>
#include<string.h>
#include<ctype.h>
//char stack
char stack[25];
int top = -1;
void push(char item) {
stack[++top] = item;
}
char pop() {
return stack[top--];
}
//returns precedence of operators
int precedence(char symbol) {
switch(symbol) {
case '+':
case '-':
return 2;
break;
case '*':
case '/':
return 3;
break;
case '^':
return 4;
break;
case '(':
case ')':
case '#':
return 1;
break;
}
}
//check whether the symbol is operator?
int isOperator(char symbol) {
switch(symbol) {
case '+':
case '-':
case '*':
case '/':
case '^':
case '(':
case ')':
return 1;
break;
default:
return 0;
}
}
//converts infix expression to postfix
void convert(char infix[],char postfix[]) {
int i,symbol,j = 0;
stack[++top] = '#';
for(i = 0;i<strlen(infix);i++) {
symbol = infix[i];
if(isOperator(symbol) == 0) {
postfix[j] = symbol;
j++;
} else {
if(symbol == '(') {
push(symbol);
} else {
if(symbol == ')') {
while(stack[top] != '(') {
postfix[j] = pop();
j++;
}
pop(); //pop out (.
} else {
if(precedence(symbol)>precedence(stack[top])) {
push(symbol);
} else {
while(precedence(symbol)<=precedence(stack[top])) {
postfix[j] = pop();
j++;
}
push(symbol);
}
}
}
}
}
while(stack[top] != '#') {
postfix[j] = pop();
j++;
}
postfix[j]='\0'; //null terminate string.
}
//int stack
int stack_int[25];
int top_int = -1;
void push_int(int item) {
stack_int[++top_int] = item;
}
char pop_int() {
return stack_int[top_int--];
}
//evaluates postfix expression
int evaluate(char *postfix){
char ch;
int i = 0,operand1,operand2;
while( (ch = postfix[i++]) != '\0') {
if(isdigit(ch)) {
push_int(ch-'0'); // Push the operand
} else {
//Operator,pop two operands
operand2 = pop_int();
operand1 = pop_int();
switch(ch) {
case '+':
push_int(operand1+operand2);
break;
case '-':
push_int(operand1-operand2);
break;
case '*':
push_int(operand1*operand2);
break;
case '/':
push_int(operand1/operand2);
break;
}
}
}
return stack_int[top_int];
}
void main() {
char infix[25] = "1*(2+3)",postfix[25];
convert(infix,postfix);
printf("Infix expression is: %s\n" , infix);
printf("Postfix expression is: %s\n" , postfix);
printf("Evaluated expression is: %d\n" , evaluate(postfix));
}
Output
Infix expression is: 1*(2+3) Postfix expression is: 123+* Evaluated expression is: 5
// C++ Code for Expression Parsing Using Stack
#include <iostream>
#include <string>
#include <cctype>
#include <stack>
// char stack
std::stack<char> stack;
void push(char item) {
stack.push(item);
}
char pop() {
char top = stack.top();
stack.pop();
return top;
}
// returns precedence of operators
int precedence(char symbol) {
switch(symbol) {
case '+':
case '-':
return 2;
case '*':
case '/':
return 3;
case '^':
return 4;
case '(':
case ')':
case '#':
return 1;
}
return 0;
}
// check whether the symbol is an operator
int isOperator(char symbol) {
switch(symbol) {
case '+':
case '-':
case '*':
case '/':
case '^':
case '(':
case ')':
return 1;
default:
return 0;
}
}
// converts infix expression to postfix
void convert(const std::string& infix, std::string& postfix) {
int j = 0;
stack.push('#');
for (char symbol : infix) {
if (isOperator(symbol) == 0) {
postfix += symbol;
j++;
} else {
if (symbol == '(') {
push(symbol);
} else {
if (symbol == ')') {
while (stack.top() != '(') {
postfix += pop();
j++;
}
stack.pop(); // pop out '('
} else {
if (precedence(symbol) > precedence(stack.top())) {
push(symbol);
} else {
while (precedence(symbol) <= precedence(stack.top())) {
postfix += pop();
j++;
}
push(symbol);
}
}
}
}
}
while (stack.top() != '#') {
postfix += pop();
j++;
}
postfix[j] = '\0'; // null terminate string
}
// evaluates postfix expression
int evaluate(const std::string& postfix) {
std::stack<int> stack_int;
int operand1, operand2;
for (char ch : postfix) {
if (std::isdigit(ch)) {
stack_int.push(ch - '0'); // Push the operand
} else {
// Operator, pop two operands
operand2 = stack_int.top();
stack_int.pop();
operand1 = stack_int.top();
stack_int.pop();
switch (ch) {
case '+':
stack_int.push(operand1 + operand2);
break;
case '-':
stack_int.push(operand1 - operand2);
break;
case '*':
stack_int.push(operand1 * operand2);
break;
case '/':
stack_int.push(operand1 / operand2);
break;
}
}
}
return stack_int.top();
}
int main() {
std::string infix = "1*(2+3)", postfix;
convert(infix, postfix);
std::cout << "Infix expression is: " << infix << std::endl;
std::cout << "Postfix expression is: " << postfix << std::endl;
std::cout << "Evaluated expression is: " << evaluate(postfix) << std::endl;
return 0;
}
Output
Infix expression is: 1*(2+3) Postfix expression is: 123+* Evaluated expression is: 5
// Java Code for Expression Parsing Using Stack
import java.util.Stack;
public class Main {
// char stack
static Stack<Character> stack = new Stack<>();
static void push(char item) {
stack.push(item);
}
static char pop() {
return stack.pop();
}
// returns precedence of operators
static int precedence(char symbol) {
switch (symbol) {
case '+':
case '-':
return 2;
case '*':
case '/':
return 3;
case '^':
return 4;
case '(':
case ')':
case '#':
return 1;
}
return 0;
}
// check whether the symbol is an operator
static int isOperator(char symbol) {
switch (symbol) {
case '+':
case '-':
case '*':
case '/':
case '^':
case '(':
case ')':
return 1;
default:
return 0;
}
}
// converts infix expression to postfix
static void convert(String infix, StringBuilder postfix) {
int j = 0;
stack.push('#');
for (char symbol : infix.toCharArray()) {
if (isOperator(symbol) == 0) {
postfix.append(symbol);
j++;
} else {
if (symbol == '(') {
push(symbol);
} else {
if (symbol == ')') {
while (stack.peek() != '(') {
postfix.append(pop());
j++;
}
stack.pop(); // pop out '('
} else {
if (precedence(symbol) > precedence(stack.peek())) {
push(symbol);
} else {
while (precedence(symbol) <= precedence(stack.peek())) {
postfix.append(pop());
j++;
}
push(symbol);
}
}
}
}
}
while (stack.peek() != '#') {
postfix.append(pop());
j++;
}
}
// evaluates postfix expression
static int evaluate(String postfix) {
Stack<Integer> stackInt = new Stack<>();
int operand1, operand2;
for (char ch : postfix.toCharArray()) {
if (Character.isDigit(ch)) {
stackInt.push(ch - '0'); // Push the operand
} else {
// Operator, pop two operands
operand2 = stackInt.pop();
operand1 = stackInt.pop();
switch (ch) {
case '+':
stackInt.push(operand1 + operand2);
break;
case '-':
stackInt.push(operand1 - operand2);
break;
case '*':
stackInt.push(operand1 * operand2);
break;
case '/':
stackInt.push(operand1 / operand2);
break;
}
}
}
return stackInt.peek();
}
public static void main(String[] args) {
String infix = "1*(2+3)";
StringBuilder postfix = new StringBuilder();
convert(infix, postfix);
System.out.println("Infix expression is: " + infix);
System.out.println("Postfix expression is: " + postfix);
System.out.println("Evaluated expression is: " + evaluate(postfix.toString()));
}
}
Output
Infix expression is: 1*(2+3) Postfix expression is: 123+* Evaluated expression is: 5
class Main:
stack = []
@staticmethod
def push(item):
Main.stack.append(item)
@staticmethod
def pop():
return Main.stack.pop()
#returns precedence of operators
@staticmethod
def precedence(symbol):
if symbol in ['+', '-']:
return 2
elif symbol in ['*', '/']:
return 3
elif symbol == '^':
return 4
elif symbol in ['(', ')', '#']:
return 1
return 0
#check whether the symbol is an operator
@staticmethod
def is_operator(symbol):
return symbol in ['+', '-', '*', '/', '^', '(', ')']
@staticmethod
def convert(infix):
postfix = ""
j = 0
Main.push('#')
for symbol in infix:
if not Main.is_operator(symbol):
postfix += symbol
j += 1
else:
if symbol == '(':
Main.push(symbol)
else:
if symbol == ')':
while Main.stack[-1] != '(':
postfix += Main.pop()
j += 1
Main.pop() # pop out '('
else:
if Main.precedence(symbol) > Main.precedence(Main.stack[-1]):
Main.push(symbol)
else:
while Main.precedence(symbol) <= Main.precedence(Main.stack[-1]):
postfix += Main.pop()
j += 1
Main.push(symbol)
while Main.stack[-1] != '#':
postfix += Main.pop()
j += 1
return postfix
@staticmethod
def evaluate(postfix):
stack_int = []
for ch in postfix:
if ch.isdigit():
stack_int.append(int(ch))
else:
operand2 = stack_int.pop()
operand1 = stack_int.pop()
if ch == '+':
stack_int.append(operand1 + operand2)
elif ch == '-':
stack_int.append(operand1 - operand2)
elif ch == '*':
stack_int.append(operand1 * operand2)
elif ch == '/':
stack_int.append(operand1 / operand2)
return stack_int[0]
@staticmethod
def main():
infix = "1*(2+3)"
postfix = Main.convert(infix)
print("Infix expression is:", infix)
print("Postfix expression is:", postfix)
print("Evaluated expression is:", Main.evaluate(postfix))
Main.main()
Output
Infix expression is: 1*(2+3) Postfix expression is: 123+* Evaluated expression is: 5
Queue Data Structure
Queue, like Stack, is also an abstract data structure. The thing that makes queue different from stack is that a queue is open at both its ends. Hence, it follows FIFO (First-In-First-Out) structure, i.e. the data item inserted first will also be accessed first. The data is inserted into the queue through one end and deleted from it using the other end.
A real-world example of queue can be a single-lane one-way road, where the vehicle enters first, exits first. More real-world examples can be seen as queues at the ticket windows and bus-stops.
Representation of Queues
Similar to the stack ADT, a queue ADT can also be implemented using arrays, linked lists, or pointers. As a small example in this tutorial, we implement queues using a one-dimensional array.
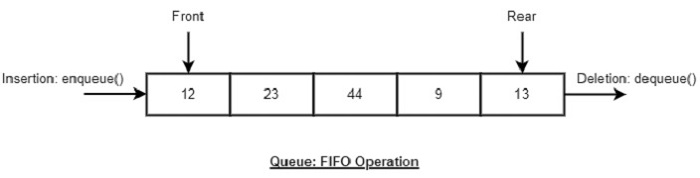
Basic Operations
Queue operations also include initialization of a queue, usage and permanently deleting the data from the memory.
The most fundamental operations in the queue ADT include: enqueue(), dequeue(), peek(), isFull(), isEmpty(). These are all built-in operations to carry out data manipulation and to check the status of the queue.
Queue uses two pointers − front and rear. The front pointer accesses the data from the front end (helping in enqueueing) while the rear pointer accesses data from the rear end (helping in dequeuing).
Insertion operation: enqueue()
The enqueue() is a data manipulation operation that is used to insert elements into the stack. The following algorithm describes the enqueue() operation in a simpler way.
Algorithm
1 START 2 Check if the queue is full. 3 If the queue is full, produce overflow error and exit. 4 If the queue is not full, increment rear pointer to point the next empty space. 5 Add data element to the queue location, where the rear is pointing. 6 return success. 7 END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
bool isEmpty(){
return itemCount == 0;
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue: 3 5 9 1 12 15
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
bool isEmpty(){
return itemCount == 0;
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue: 3 5 9 1 12 15
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.add(6);
q.add(1);
q.add(8);
q.add(4);
q.add(7);
System.out.println("The queue is: " + q);
}
}
Output
The queue is: [6, 1, 8, 4, 7]
class Queue:
def __init__(self):
self.queue = list()
def __str__(self):
return str(self.queue)
def addtoqueue(self,data):
# Insert method to add element
if data not in self.queue:
self.queue.insert(0,data)
return True
return False
q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
Output
Queue: ['66', '12', '48', '24', '36']
Deletion Operation: dequeue()
The dequeue() is a data manipulation operation that is used to remove elements from the stack. The following algorithm describes the dequeue() operation in a simpler way.
Algorithm
1 START 2 Check if the queue is empty. 3 If the queue is empty, produce underflow error and exit. 4 If the queue is not empty, access the data where front is pointing. 5 Increment front pointer to point to the next available data element. 6 Return success. 7 END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
bool isEmpty(){
return itemCount == 0;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
// remove one item
int num = removeData();
printf("\nElement removed: %d\n",num);
printf("Updated Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue: 3 5 9 1 12 15 Element removed: 3 Updated Queue: 5 9 1 12 15
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
bool isEmpty(){
return itemCount == 0;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
// remove one item
int num = removeData();
printf("\nElement removed: %d\n",num);
printf("Updated Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue: 3 5 9 1 12 15 Element removed: 3 Updated Queue: 5 9 1 12 15
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.add(6);
q.add(1);
q.add(8);
q.add(4);
q.add(7);
System.out.println("The queue is: " + q);
int n = q.remove();
System.out.println("The element deleted is: " + n);
System.out.println("Queue after deletion: " + q);
}
}
Output
The queue is: [6, 1, 8, 4, 7] The element deleted is: 6 Queue after deletion: [1, 8, 4, 7]
class Queue:
def __init__(self):
self.queue = list()
def __str__(self):
return str(self.queue)
def addtoqueue(self,data):
# Insert method to add element
if data not in self.queue:
self.queue.insert(0,data)
return True
return False
def removefromqueue(self):
if len(self.queue)>0:
return self.queue.pop()
return ("Queue is empty")
q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
print("Element deleted from queue: ",q.removefromqueue())
Output
Queue: ['66', '12', '48', '24', '36'] Element deleted from queue: 36
The peek() Operation
The peek() is an operation which is used to retrieve the frontmost element in the queue, without deleting it. This operation is used to check the status of the queue with the help of the pointer.
Algorithm
1 START 2 Return the element at the front of the queue 3 END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isFull(){
return itemCount == MAX;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\nElement at front: %d\n",peek());
}
Output
Queue: 3 5 9 1 12 15 Element at front: 3
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isFull(){
return itemCount == MAX;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\nElement at front: %d\n",peek());
}
Output
Queue: 3 5 9 1 12 15 Element at front: 3
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.add(6);
q.add(1);
q.add(8);
q.add(4);
q.add(7);
System.out.println("The queue is: " + q);
}
}
Output
The queue is: [6, 1, 8, 4, 7]
class Queue:
def __init__(self):
self.queue = list()
def __str__(self):
return str(self.queue)
def addtoqueue(self,data):
# Insert method to add element
if data not in self.queue:
self.queue.insert(0,data)
return True
return False
def peek(self):
return self.queue[-1]
q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("Queue:")
print(q)
print("The frontmost element of the queue: ",q.peek())
Output
Queue: ['66', '12', '48', '24', '36'] The frontmost element of the queue: 36
The isFull() Operation
The isFull() operation verifies whether the stack is full.
Algorithm
1 START 2 If the count of queue elements equals the queue size, return true 3 Otherwise, return false 4 END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\n");
if(isFull()) {
printf("Queue is full!\n");
}
}
Output
Queue: 3 5 9 1 12 15 Queue is full!
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isFull(){
return itemCount == MAX;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int main(){
int i;
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
insert(15);
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\n");
if(isFull()) {
printf("Queue is full!\n");
}
}
Output
Queue: 3 5 9 1 12 15 Queue is full!
import java.io.*;
public class QueueExample {
private int intArray[];
private int front;
private int rear;
private int itemCount;
private int MAX;
QueueExample(int size) {
intArray = new int[size];
front = 0;
rear = -1;
MAX = size;
itemCount = 0;
}
public boolean isFull() {
return itemCount == MAX;
}
public void insert(int key) {
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = key;
itemCount++;
}
}
public static void main (String[] args) {
QueueExample q = new QueueExample(5);
q.insert(1); // inserting 1 in the stack
q.insert(2);
q.insert(3);
q.insert(4);
q.insert(5);
System.out.println("Stack Full? " + q.isFull());
}
}
Output
Stack Full? true
#python code for isFull in Queue
MAX = 6
intArray = [None] * MAX
front = 0
rear = -1
itemCount = 0
def isFull():
return itemCount == MAX
def insert(data):
global rear, itemCount
if not isFull():
if rear == MAX-1:
rear = -1
rear += 1
intArray[rear] = data
itemCount += 1
#inserting 5 items into the Queue
insert(3)
insert(5)
insert(9)
insert(1)
insert(12)
insert(15)
print("Queue: ", end="")
for i in range(MAX):
print(intArray[i], end=" ")
print()
if isFull():
print("Queue is full!")
Output
Queue: 3 5 9 1 12 15 Queue is full!
The isEmpty() operation
The isEmpty() operation verifies whether the stack is empty. This operation is used to check the status of the stack with the help of top pointer.
Algorithm
1 START 2 If the count of queue elements equals zero, return true 3 Otherwise, return false 4 END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
return itemCount == 0;
}
int main(){
int i;
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\n");
if(isEmpty()) {
printf("Queue is Empty!\n");
}
}
Output
Queue: 0 0 0 0 0 0 Queue is Empty!
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
bool isEmpty(){
return itemCount == 0;
}
int main(){
int i;
printf("Queue: ");
for(i = 0; i < MAX; i++)
printf("%d ", intArray[i]);
printf("\n");
if(isEmpty()) {
printf("Queue is Empty!\n");
}
}
Output
Queue: 0 0 0 0 0 0 Queue is Empty!
import java.io.*;
public class QueueExample {
private int intArray[];
private int front;
private int rear;
private int itemCount;
private int MAX;
QueueExample(int size) {
intArray = new int[size];
front = 0;
rear = -1;
MAX = size;
itemCount = 0;
}
public boolean isEmpty() {
return itemCount == 0;
}
public static void main (String[] args) {
QueueExample q = new QueueExample(5);
System.out.println("Stack Empty? " + q.isEmpty());
}
}
Output
Stack Empty? true
#python code for isFull in Queue
MAX = 6
intArray = [None] * MAX
front = 0
rear = -1
itemCount = 0
def isEmpty():
return itemCount == 0
print("Queue: ", end="")
for i in range(MAX):
print(intArray[i], end=" ")
print()
if isEmpty():
print("Queue is empty!")
Output
Queue: None None None None None None Queue is empty!
Implementation of Queue
In this chapter, the algorithm implementation of the Queue data structure is performed in four programming languages.
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isEmpty(){
return itemCount == 0;
}
bool isFull(){
return itemCount == MAX;
}
int size(){
return itemCount;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main(){
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// front : 0
// rear : 4
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 3 5 9 1 12
insert(15);
// front : 0
// rear : 5
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 3 5 9 1 12 15
if(isFull()) {
printf("Queue is full!\n");
}
// remove one item
int num = removeData();
printf("Element removed: %d\n",num);
// front : 1
// rear : 5
// -------------------
// index : 1 2 3 4 5
// -------------------
// queue : 5 9 1 12 15
// insert more items
insert(16);
// front : 1
// rear : -1
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
// As queue is full, elements will not be inserted.
insert(17);
insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
printf("Element at front: %d\n",peek());
printf("----------------------\n");
printf("index : 5 4 3 2 1 0\n");
printf("----------------------\n");
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue is full! Element removed: 3 Element at front: 5 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 5 9 1 12 15 16
#include <iostream>
#include <string>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isEmpty(){
return itemCount == 0;
}
bool isFull(){
return itemCount == MAX;
}
int size(){
return itemCount;
}
void insert(int data){
if(!isFull()) {
if(rear == MAX-1) {
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX) {
front = 0;
}
itemCount--;
return data;
}
int main(){
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// front : 0
// rear : 4
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 3 5 9 1 12
insert(15);
// front : 0
// rear : 5
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 3 5 9 1 12 15
if(isFull()) {
printf("Queue is full!\n");
}
// remove one item
int num = removeData();
printf("Element removed: %d\n",num);
// front : 1
// rear : 5
// -------------------
// index : 1 2 3 4 5
// -------------------
// queue : 5 9 1 12 15
// insert more items
insert(16);
// front : 1
// rear : -1
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
// As queue is full, elements will not be inserted.
insert(17);
insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
printf("Element at front: %d\n",peek());
printf("----------------------\n");
printf("index : 5 4 3 2 1 0\n");
printf("----------------------\n");
printf("Queue: ");
while(!isEmpty()) {
int n = removeData();
printf("%d ",n);
}
}
Output
Queue is full! Element removed: 3 Element at front: 5 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 5 9 1 12 15 16
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<Integer> q = new LinkedList<>();
q.add(6);
q.add(1);
q.add(8);
q.add(4);
q.add(7);
System.out.println("The queue is: " + q);
int n = q.remove();
System.out.println("The element deleted is: " + n);
System.out.println("Queue after deletion: " + q);
int size = q.size();
System.out.println("Size of the queue is: " + size);
}
}
Output
The queue is: [6, 1, 8, 4, 7]The element deleted is: 6 Queue after deletion: [1, 8, 4, 7] Size of the queue is: 4
class Queue:
def __init__(self):
self.queue = list()
def addtoqueue(self,data):
# Insert method to add element
if data not in self.queue:
self.queue.insert(0,data)
return True
return False
def size(self):
return len(self.queue)
def removefromqueue(self):
if len(self.queue)>0:
return self.queue.pop()
return ("Queue is empty")
q = Queue()
q.addtoqueue("36")
q.addtoqueue("24")
q.addtoqueue("48")
q.addtoqueue("12")
q.addtoqueue("66")
print("size of the queue: ",q.size())
print("Element deleted from queue: ",q.removefromqueue())
print("size of the queue after deletion: ",q.size())
Output
size of the queue: 5 Element deleted from queue: 36 size of the queue after deletion: 4
Graph Data Structure
A graph is an abstract data type (ADT) that consists of a set of objects that are connected to each other via links. These objects are called vertices and the links are called edges.
Usually, a graph is represented as G = {V, E}, where G is the graph space, V is the set of vertices and E is the set of edges. If E is empty, the graph is known as a forest.
Before we proceed further, let's familiarize ourselves with some important terms −
Vertex − Each node of the graph is represented as a vertex. In the following example, the labelled circle represents vertices. Thus, A to G are vertices. We can represent them using an array as shown in the following image. Here A can be identified by index 0. B can be identified using index 1 and so on.
Edge − Edge represents a path between two vertices or a line between two vertices. In the following example, the lines from A to B, B to C, and so on represents edges. We can use a two-dimensional array to represent an array as shown in the following image. Here AB can be represented as 1 at row 0, column 1, BC as 1 at row 1, column 2 and so on, keeping other combinations as 0.
Adjacency − Two node or vertices are adjacent if they are connected to each other through an edge. In the following example, B is adjacent to A, C is adjacent to B, and so on.
Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.
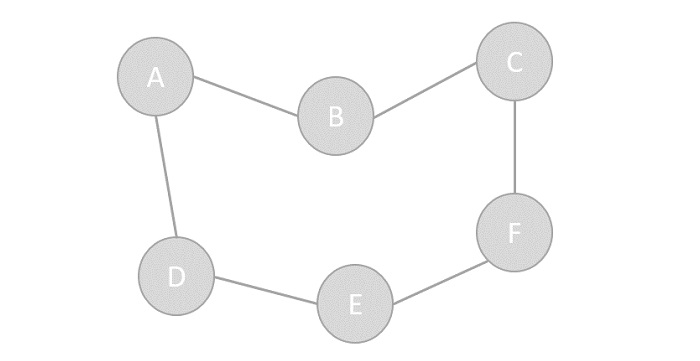
Operations of Graphs
The primary operations of a graph include creating a graph with vertices and edges, and displaying the said graph. However, one of the most common and popular operation performed using graphs are Traversal, i.e. visiting every vertex of the graph in a specific order.
There are two types of traversals in Graphs −
Depth First Search Traversal
Breadth First Search Traversal
Depth First Search Traversal
Depth First Search is a traversal algorithm that visits all the vertices of a graph in the decreasing order of its depth. In this algorithm, an arbitrary node is chosen as the starting point and the graph is traversed back and forth by marking unvisited adjacent nodes until all the vertices are marked.
The DFS traversal uses the stack data structure to keep track of the unvisited nodes.
Breadth First Search Traversal
Breadth First Search is a traversal algorithm that visits all the vertices of a graph present at one level of the depth before moving to the next level of depth. In this algorithm, an arbitrary node is chosen as the starting point and the graph is traversed by visiting the adjacent vertices on the same depth level and marking them until there is no vertex left.
The DFS traversal uses the queue data structure to keep track of the unvisited nodes.
Representation of Graphs
While representing graphs, we must carefully depict the elements (vertices and edges) present in the graph and the relationship between them. Pictorially, a graph is represented with a finite set of nodes and connecting links between them. However, we can also represent the graph in other most commonly used ways, like −
Adjacency Matrix
Adjacency List
Adjacency Matrix
The Adjacency Matrix is a VV matrix where the values are filled with either 0 or 1. If the link exists between Vi and Vj, it is recorded 1; otherwise, 0.
For the given graph below, let us construct an adjacency matrix −
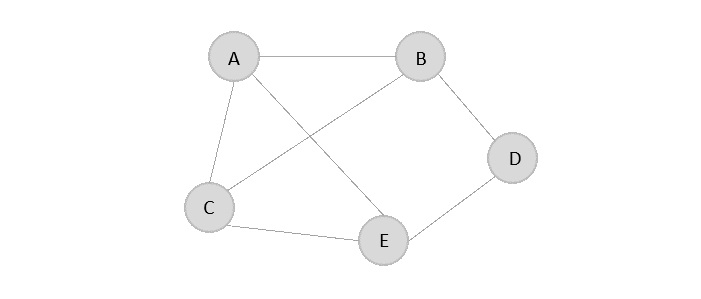
The adjacency matrix is −
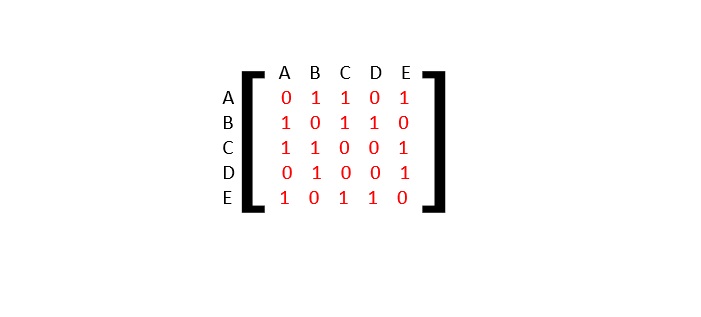
Adjacency List
The adjacency list is a list of the vertices directly connected to the other vertices in the graph.

The adjacency list is −
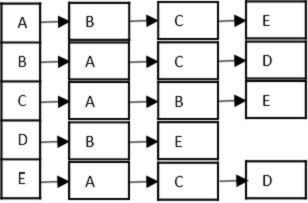
Types of graph
There are two basic types of graph −
Directed Graph
Undirected Graph
Directed graph, as the name suggests, consists of edges that possess a direction that goes either away from a vertex or towards the vertex. Undirected graphs have edges that are not directed at all.
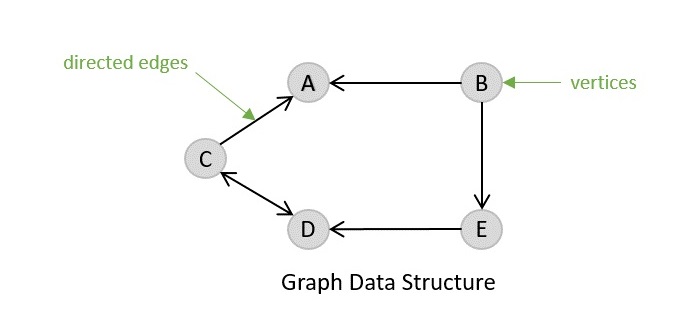
Directed Graph
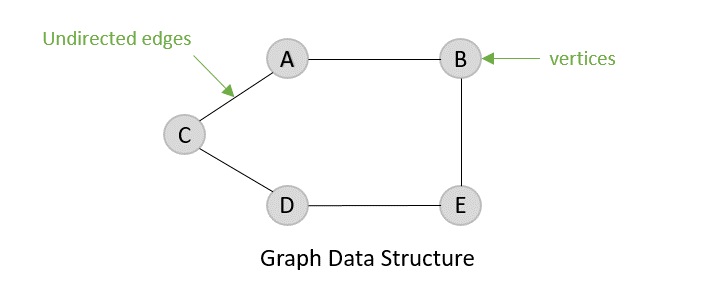
Undirected Graph
Spanning Tree
A spanning tree is a subset of an undirected graph that contains all the vertices of the graph connected with the minimum number of edges in the graph. Precisely, the edges of the spanning tree is a subset of the edges in the original graph.
If all the vertices are connected in a graph, then there exists at least one spanning tree. In a graph, there may exist more than one spanning tree.
Properties
A spanning tree does not have any cycle.
Any vertex can be reached from any other vertex.
Example
In the following graph, the highlighted edges form a spanning tree.
Minimum Spanning Tree
A Minimum Spanning Tree (MST) is a subset of edges of a connected weighted undirected graph that connects all the vertices together with the minimum possible total edge weight. To derive an MST, Prims algorithm or Kruskals algorithm can be used. Hence, we will discuss Prims algorithm in this chapter.
As we have discussed, one graph may have more than one spanning tree. If there are n number of vertices, the spanning tree should have number of edges. In this context, if each edge of the graph is associated with a weight and there exists more than one spanning tree, we need to find the minimum spanning tree of the graph.
Moreover, if there exist any duplicate weighted edges, the graph may have multiple minimum spanning tree.
In the above graph, we have shown a spanning tree though its not the minimum spanning tree. The cost of this spanning tree is (5+7+3+3+5+8+3+4)=38.
Shortest Path
The shortest path in a graph is defined as the minimum cost route from one vertex to another. This is most commonly seen in weighted directed graphs but are also applicable to undirected graphs.
A popular real-world application of finding the shortest path in a graph is a map. Navigation is made easier and simpler with the various shortest path algorithms where destinations are considered vertices of the graph and routes are the edges. The two common shortest path algorithms are −
Dijkstras Shortest Path Algorithm
Bellman Fords Shortest Path Algorithm
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include<stdlib.h>
#include <stdlib.h>
#define V 5
// Maximum number of vertices in the graph
struct graph {
// declaring graph data structure
struct vertex *point[V];
};
struct vertex {
// declaring vertices
int end;
struct vertex *next;
};
struct Edge {
// declaring edges
int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
int i;
struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
for (i = 0; i < V; i++) {
graph->point[i] = NULL;
}
for (i = 0; i < x; i++) {
int start = edges[i].start;
int end = edges[i].end;
struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
v->end = end;
v->next = graph->point[start];
graph->point[start] = v;
}
return graph;
}
int main (){
struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
int n = sizeof (edges) / sizeof (edges[0]);
struct graph *graph = create_graph (edges, n);
int i;
for (i = 0; i < V; i++) {
struct vertex *ptr = graph->point[i];
while (ptr != NULL) {
printf ("(%d -> %d)\t", i, ptr->end);
ptr = ptr->next;
}
printf ("\n");
}
return 0;
}
Output
(1 -> 3) (1 -> 0) (2 -> 1) (2 -> 0) (3 -> 2) (3 -> 0) (4 -> 2) (4 -> 1)
#include <bits/stdc++.h>
using namespace std;
#define V 5
// Maximum number of vertices in the graph
struct graph {
// declaring graph data structure
struct vertex *point[V];
};
struct vertex {
// declaring vertices
int end;
struct vertex *next;
};
struct Edge {
// declaring edges
int end, start;
};
struct graph *create_graph (struct Edge edges[], int x){
int i;
struct graph *graph = (struct graph *) malloc (sizeof (struct graph));
for (i = 0; i < V; i++) {
graph->point[i] = NULL;
}
for (i = 0; i < x; i++) {
int start = edges[i].start;
int end = edges[i].end;
struct vertex *v = (struct vertex *) malloc (sizeof (struct vertex));
v->end = end;
v->next = graph->point[start];
graph->point[start] = v;
}
return graph;
}
int main (){
struct Edge edges[] = { {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 4}, {2, 4}, {2, 3}, {3, 1} };
int n = sizeof (edges) / sizeof (edges[0]);
struct graph *graph = create_graph (edges, n);
int i;
for (i = 0; i < V; i++) {
struct vertex *ptr = graph->point[i];
while (ptr != NULL) {
cout << "(" << i << " -> " << ptr->end << ")\t";
ptr = ptr->next;
}
cout << endl;
}
return 0;
}
Output
(1 -> 3) (1 -> 0) (2 -> 1) (2 -> 0) (3 -> 2) (3 -> 0) (4 -> 2) (4 -> 1)
import java.util.*;
//class to store edges of the graph
class Edge {
int src, dest;
Edge(int src, int dest) {
this.src = src;
this.dest = dest;
}
}
// Graph class
public class Graph {
// node of adjacency list
static class vertex {
int v;
vertex(int v) {
this.v = v;
}
};
// define adjacency list to represent the graph
List<List<vertex>> adj_list = new ArrayList<>();
//Graph Constructor
public Graph(List<Edge> edges){
// adjacency list memory allocation
for (int i = 0; i < edges.size(); i++)
adj_list.add(i, new ArrayList<>());
// add edges to the graph
for (Edge e : edges){
// allocate new node in adjacency List from src to dest
adj_list.get(e.src).add(new vertex(e.dest));
}
}
public static void main (String[] args) {
// define edges of the graph
List<Edge> edges = Arrays.asList(new Edge(0, 1),new Edge(0, 2),
new Edge(0, 3),new Edge(1, 2), new Edge(1, 4),
new Edge(2, 4), new Edge(2, 3),new Edge(3, 1));
// call graph class Constructor to construct a graph
Graph graph = new Graph(edges);
// print the graph as an adjacency list
int src = 0;
int lsize = graph.adj_list.size();
System.out.println("The graph created is:");
while (src < lsize) {
//traverse through the adjacency list and print the edges
for (vertex edge : graph.adj_list.get(src)) {
System.out.print(src + " -> " + edge.v + "\t");
}
System.out.println();
src++;
}
}
}
Output
The graph created is: 0 -> 1 0 -> 2 0 -> 3 1 -> 2 1 -> 4 2 -> 4 2 -> 3 3 -> 1
#Python code for Graph Data Struture
V = 5
#Maximum number of vertices in th graph
#Declaring vertices
class Vertex:
def __init__(self, end):
self.end = end
self.next = None
#Declaring Edges
class Edge:
def __init__(self, start, end):
self.start = start
self.end = end
#Declaring graph data structure
class Graph:
def __init__(self):
self.point = [None] * V
def create_graph(edges, x):
graph = Graph()
for i in range(V):
graph.point[i] = None
for i in range(x):
start = edges[i].start
end = edges[i].end
v = Vertex(end)
v.next = graph.point[start]
graph.point[start] = v
return graph
edges = [Edge(0, 1), Edge(0, 2), Edge(0, 3), Edge(1, 2), Edge(1, 4), Edge(2, 4), Edge(2, 3), Edge(3, 1)]
n = len(edges)
graph = create_graph(edges, n)
#Range
for i in range(V):
ptr = graph.point[i]
while ptr is not None:
print("({} -> {})".format(i, ptr.end), end="\t")
ptr = ptr.next
print()
Output
(0 -> 3) (0 -> 2) (0 -> 1) (1 -> 4) (1 -> 2) (2 -> 3) (2 -> 4) (3 -> 1)
Depth First Traversal
Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack to remember to get the next vertex to start a search, when a dead end occurs in any iteration.
As in the example given above, DFS algorithm traverses from S to A to D to G to E to B first, then to F and lastly to C. It employs the following rules.
Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack.
Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the stack, which do not have adjacent vertices.)
Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty.
| Step | Traversal | Description |
|---|---|---|
| 1 | 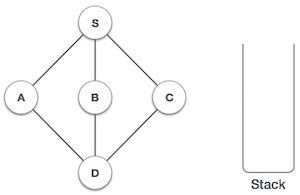 |
Initialize the stack. |
| 2 | 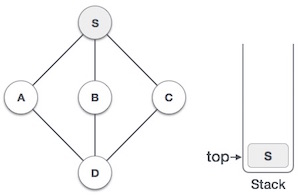 |
Mark S as visited and put it onto the stack. Explore any unvisited adjacent node from S. We have three nodes and we can pick any of them. For this example, we shall take the node in an alphabetical order. |
| 3 | 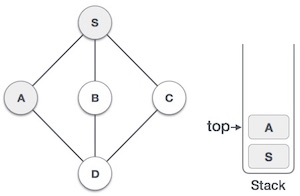 |
Mark A as visited and put it onto the stack. Explore any unvisited adjacent node from A. Both S and D are adjacent to A but we are concerned for unvisited nodes only. |
| 4 | 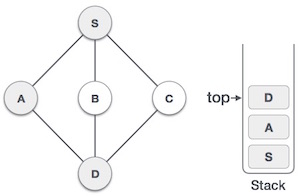 |
Visit D and mark it as visited and put onto the stack. Here, we have B and C nodes, which are adjacent to D and both are unvisited. However, we shall again choose in an alphabetical order. |
| 5 | 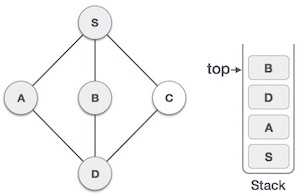 |
We choose B, mark it as visited and put onto the stack. Here B does not have any unvisited adjacent node. So, we pop B from the stack. |
| 6 | 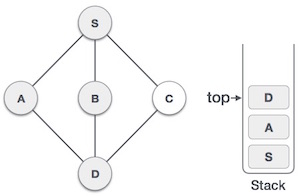 |
We check the stack top for return to the previous node and check if it has any unvisited nodes. Here, we find D to be on the top of the stack. |
| 7 | 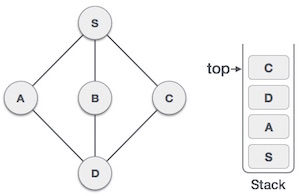 |
Only unvisited adjacent node is from D is C now. So we visit C, mark it as visited and put it onto the stack. |
As C does not have any unvisited adjacent node so we keep popping the stack until we find a node that has an unvisited adjacent node. In this case, there's none and we keep popping until the stack is empty.
Example
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Vertex {
char label;
bool visited;
};
//stack variables
int stack[MAX];
int top = -1;
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//stack functions
void push(int item) {
stack[++top] = item;
}
int pop() {
return stack[top--];
}
int peek() {
return stack[top];
}
bool isStackEmpty() {
return top == -1;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
printf("%c ",lstVertices[vertexIndex]->label);
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
int i;
for(i = 0; i < vertexCount; i++) {
if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false) {
return i;
}
}
return -1;
}
void depthFirstSearch() {
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//push vertex index in stack
push(0);
while(!isStackEmpty()) {
//get the unvisited vertex of vertex which is at top of the stack
int unvisitedVertex = getAdjUnvisitedVertex(peek());
//no adjacent vertex found
if(unvisitedVertex == -1) {
pop();
} else {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
push(unvisitedVertex);
}
}
//stack is empty, search is complete, reset the visited flag
for(i = 0;i < vertexCount;i++) {
lstVertices[i]->visited = false;
}
}
int main() {
int i, j;
for(i = 0; i < MAX; i++) { // set adjacency
for(j = 0; j < MAX; j++) // matrix to 0
adjMatrix[i][j] = 0;
}
addVertex('S'); // 0
addVertex('A'); // 1
addVertex('B'); // 2
addVertex('C'); // 3
addVertex('D'); // 4
addEdge(0, 1); // S - A
addEdge(0, 2); // S - B
addEdge(0, 3); // S - C
addEdge(1, 4); // A - D
addEdge(2, 4); // B - D
addEdge(3, 4); // C - D
printf("Depth First Search: ");
depthFirstSearch();
return 0;
}
Output
Depth First Search: S A D B C
//C++ code for Depth First Traversal
#include <iostream>
#include <array>
#include <vector>
constexpr int MAX = 5;
struct Vertex {
char label;
bool visited;
};
//stack variables
std::array<int, MAX> stack;
int top = -1;
//graph variables
//array of vertices
std::array<Vertex*, MAX> lstVertices;
//adjacency matrix
std::array<std::array<int, MAX>, MAX> adjMatrix;
//vertex count
int vertexCount = 0;
//stack functions
void push(int item) {
stack[++top] = item;
}
int pop() {
return stack[top--];
}
int peek() {
return stack[top];
}
bool isStackEmpty() {
return top == -1;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
Vertex* vertex = new Vertex;
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start, int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
std::cout << lstVertices[vertexIndex]->label << " ";
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
for (int i = 0; i < vertexCount; i++) {
if (adjMatrix[vertexIndex][i] == 1 && !lstVertices[i]->visited) {
return i;
}
}
return -1;
}
//mark first node as visited
void depthFirstSearch() {
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//push vertex index in stack
push(0);
while (!isStackEmpty()) {
//get the unvisited vertex of vertex which is at top of the stack
int unvisitedVertex = getAdjUnvisitedVertex(peek());
//no adjacent vertex found
if (unvisitedVertex == -1) {
pop();
} else {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
push(unvisitedVertex);
}
}
//stack is empty, search is complete, reset the visited flag
for (int i = 0; i < vertexCount; i++) {
lstVertices[i]->visited = false;
}
}
int main() {
for (int i = 0; i < MAX; i++) { //set adjacency
for (int j = 0; j < MAX; j++) { // matrix to 0
adjMatrix[i][j] = 0;
}
}
addVertex('S');
addVertex('A');
addVertex('B');
addVertex('C');
addVertex('D');
addEdge(0, 1);
addEdge(0, 2);
addEdge(0, 3);
addEdge(1, 4);
addEdge(2, 4);
addEdge(3, 4);
std::cout << "Depth First Search: ";
depthFirstSearch();
return 0;
}
Output
Depth First Search: S A D B C
//Java program for Depth First Traversal
public class DepthFirstSearch {
private static final int MAX = 5;
private static class Vertex {
char label;
boolean visited;
}
private static int[] stack = new int[MAX];
private static int top = -1;
private static Vertex[] lstVertices = new Vertex[MAX];
private static int[][] adjMatrix = new int[MAX][MAX];
private static int vertexCount = 0;
private static void push(int item) {
stack[++top] = item;
}
private static int pop() {
return stack[top--];
}
private static int peek() {
return stack[top];
}
private static boolean isStackEmpty() {
return top == -1;
}
private static void addVertex(char label) {
Vertex vertex = new Vertex();
vertex.label = label;
vertex.visited = false;
lstVertices[vertexCount++] = vertex;
}
private static void addEdge(int start, int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
private static void displayVertex(int vertexIndex) {
System.out.print(lstVertices[vertexIndex].label + " ");
}
private static int getAdjUnvisitedVertex(int vertexIndex) {
for (int i = 0; i < vertexCount; i++) {
if (adjMatrix[vertexIndex][i] == 1 && !lstVertices[i].visited) {
return i;
}
}
return -1;
}
private static void depthFirstSearch() {
lstVertices[0].visited = true;
displayVertex(0);
push(0);
while (!isStackEmpty()) {
int unvisitedVertex = getAdjUnvisitedVertex(peek());
if (unvisitedVertex == -1) {
pop();
} else {
lstVertices[unvisitedVertex].visited = true;
displayVertex(unvisitedVertex);
push(unvisitedVertex);
}
}
for (int i = 0; i < vertexCount; i++) {
lstVertices[i].visited = false;
}
}
public static void main(String[] args) {
for (int i = 0; i < MAX; i++) {
for (int j = 0; j < MAX; j++) {
adjMatrix[i][j] = 0;
}
}
addVertex('S'); // 0
addVertex('A'); // 1
addVertex('B'); // 2
addVertex('C'); // 3
addVertex('D'); // 4
addEdge(0, 1); // S - A
addEdge(0, 2); // S - B
addEdge(0, 3); // S - C
addEdge(1, 4); // A - D
addEdge(2, 4); // B - D
addEdge(3, 4); // C - D
System.out.print("Depth First Search: ");
depthFirstSearch();
}
}
Output
Depth First Search: S A D B C
#Python program for Depth First Traversal
MAX = 5
class Vertex:
def __init__(self, label):
self.label = label
self.visited = False
#stack variables
stack = []
top = -1
#graph variables
#array of vertices
lstVertices = [None] * MAX
#adjacency matrix
adjMatrix = [[0] * MAX for _ in range(MAX)]
#vertex count
vertexCount = 0
#stack functions
def push(item):
global top
top += 1
stack.append(item)
def pop():
global top
item = stack[top]
del stack[top]
top -= 1
return item
def peek():
return stack[top]
def isStackEmpty():
return top == -1
#graph functions
#add vertex to the vertex list
def addVertex(label):
global vertexCount
vertex = Vertex(label)
lstVertices[vertexCount] = vertex
vertexCount += 1
#add edge to edge array
def addEdge(start, end):
adjMatrix[start][end] = 1
adjMatrix[end][start] = 1
#Display the Vertex
def displayVertex(vertexIndex):
print(lstVertices[vertexIndex].label, end=' ')
def getAdjUnvisitedVertex(vertexIndex):
for i in range(vertexCount):
if adjMatrix[vertexIndex][i] == 1 and not lstVertices[i].visited:
return i
return -1
def depthFirstSearch():
lstVertices[0].visited = True
displayVertex(0)
push(0)
while not isStackEmpty():
unvisitedVertex = getAdjUnvisitedVertex(peek())
if unvisitedVertex == -1:
pop()
else:
lstVertices[unvisitedVertex].visited = True
displayVertex(unvisitedVertex)
push(unvisitedVertex)
for i in range(vertexCount):
lstVertices[i].visited = False
for i in range(MAX):
for j in range(MAX):
adjMatrix[i][j] = 0
addVertex('S') # 0
addVertex('A') # 1
addVertex('B') # 2
addVertex('C') # 3
addVertex('D') # 4
addEdge(0, 1) # S - A
addEdge(0, 2) # S - B
addEdge(0, 3) # S - C
addEdge(1, 4) # A - D
addEdge(2, 4) # B - D
addEdge(3, 4) # C - D
print("Depth First Search:", end=' ')
depthFirstSearch()
Output
Depth First Search: S A D B C
Breadth First Traversal
Breadth First Search (BFS) algorithm traverses a graph in a breadthward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration.
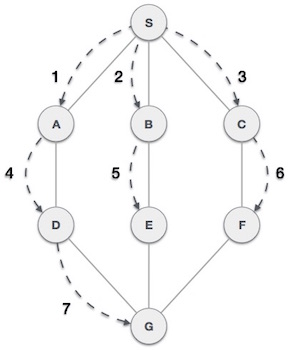
As in the example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs the following rules.
Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue.
Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.
| Step | Traversal | Description |
|---|---|---|
| 1 |  |
Initialize the queue. |
| 2 |  |
We start from visiting S (starting node), and mark it as visited. |
| 3 |  |
We then see an unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A, mark it as visited and enqueue it. |
| 4 |  |
Next, the unvisited adjacent node from S is B. We mark it as visited and enqueue it. |
| 5 | 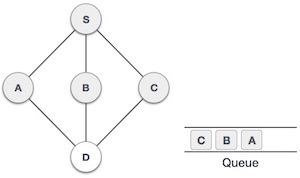 |
Next, the unvisited adjacent node from S is C. We mark it as visited and enqueue it. |
| 6 | 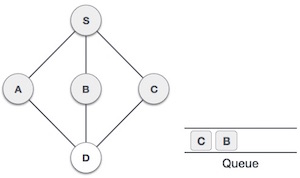 |
Now, S is left with no unvisited adjacent nodes. So, we dequeue and find A. |
| 7 | 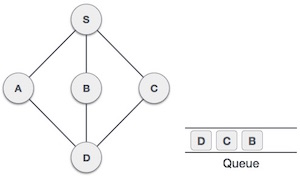 |
From A we have D as unvisited adjacent node. We mark it as visited and enqueue it. |
At this stage, we are left with no unmarked (unvisited) nodes. But as per the algorithm we keep on dequeuing in order to get all unvisited nodes. When the queue gets emptied, the program is over.
Example
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Vertex {
char label;
bool visited;
};
//queue variables
int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//queue functions
void insert(int data) {
queue[++rear] = data;
queueItemCount++;
}
int removeData() {
queueItemCount--;
return queue[front++];
}
bool isQueueEmpty() {
return queueItemCount == 0;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
printf("%c ",lstVertices[vertexIndex]->label);
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
int i;
for(i = 0; i<vertexCount; i++) {
if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
return i;
}
return -1;
}
void breadthFirstSearch() {
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//insert vertex index in queue
insert(0);
int unvisitedVertex;
while(!isQueueEmpty()) {
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = removeData();
//no adjacent vertex found
while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(i = 0;i<vertexCount;i++) {
lstVertices[i]->visited = false;
}
}
int main() {
int i, j;
for(i = 0; i<MAX; i++) { // set adjacency
for(j = 0; j<MAX; j++) // matrix to 0
adjMatrix[i][j] = 0;
}
addVertex('S'); // 0
addVertex('A'); // 1
addVertex('B'); // 2
addVertex('C'); // 3
addVertex('D'); // 4
addEdge(0, 1); // S - A
addEdge(0, 2); // S - B
addEdge(0, 3); // S - C
addEdge(1, 4); // A - D
addEdge(2, 4); // B - D
addEdge(3, 4); // C - D
printf("\nBreadth First Search: ");
breadthFirstSearch();
return 0;
}
Output
Breadth First Search: S A B C D
//C++ code for Breadth First Traversal
#include <iostream>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 5
struct Vertex {
char label;
bool visited;
};
//queue variables
int queue[MAX];
int rear = -1;
int front = 0;
int queueItemCount = 0;
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//queue functions
void insert(int data) {
queue[++rear] = data;
queueItemCount++;
}
int removeData() {
queueItemCount--;
return queue[front++];
}
bool isQueueEmpty() {
return queueItemCount == 0;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label) {
struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex) {
std::cout << lstVertices[vertexIndex]->label << " ";
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex) {
int i;
for(i = 0; i<vertexCount; i++) {
if(adjMatrix[vertexIndex][i] == 1 && lstVertices[i]->visited == false)
return i;
}
return -1;
}
void breadthFirstSearch() {
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//insert vertex index in queue
insert(0);
int unvisitedVertex;
while(!isQueueEmpty()) {
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = removeData();
//no adjacent vertex found
while((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(i = 0;i<vertexCount;i++) {
lstVertices[i]->visited = false;
}
}
int main() {
int i, j;
for(i = 0; i<MAX; i++) { // set adjacency
for(j = 0; j<MAX; j++) // matrix to 0
adjMatrix[i][j] = 0;
}
addVertex('S'); // 0
addVertex('A'); // 1
addVertex('B'); // 2
addVertex('C'); // 3
addVertex('D'); // 4
addEdge(0, 1); // S - A
addEdge(0, 2); // S - B
addEdge(0, 3); // S - C
addEdge(1, 4); // A - D
addEdge(2, 4); // B - D
addEdge(3, 4); // C - D
std::cout << "Breadth First Search: ";
breadthFirstSearch();
return 0;
}
Output
Breadth First Search: S A B C D
//Java code for Breadth First Traversal
import java.util.LinkedList;
import java.util.Queue;
class Vertex {
char label;
boolean visited;
public Vertex(char label) {
this.label = label;
visited = false;
}
}
public class Graph {
private static final int MAX = 5;
private Vertex[] lstVertices;
private int[][] adjMatrix;
private int vertexCount;
public Graph() {
lstVertices = new Vertex[MAX];
adjMatrix = new int[MAX][MAX];
vertexCount = 0;
}
private void addVertex(char label) {
Vertex vertex = new Vertex(label);
lstVertices[vertexCount++] = vertex;
}
private void addEdge(int start, int end) {
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
private void displayVertex(int vertexIndex) {
System.out.print(lstVertices[vertexIndex].label + " ");
}
private int getAdjUnvisitedVertex(int vertexIndex) {
for (int i = 0; i < vertexCount; i++) {
if (adjMatrix[vertexIndex][i] == 1 && !lstVertices[i].visited)
return i;
}
return -1;
}
private void breadthFirstSearch() {
lstVertices[0].visited = true;
displayVertex(0);
Queue<Integer> queue = new LinkedList<>();
queue.add(0);
while (!queue.isEmpty()) {
int tempVertex = queue.poll();
int unvisitedVertex;
while ((unvisitedVertex = getAdjUnvisitedVertex(tempVertex)) != -1) {
lstVertices[unvisitedVertex].visited = true;
displayVertex(unvisitedVertex);
queue.add(unvisitedVertex);
}
}
// Reset the visited flag
for (int i = 0; i < vertexCount; i++) {
lstVertices[i].visited = false;
}
}
public static void main(String[] args) {
Graph graph = new Graph();
for (int i = 0; i < MAX; i++) {
for (int j = 0; j < MAX; j++)
graph.adjMatrix[i][j] = 0;
}
graph.addVertex('S'); // 0
graph.addVertex('A'); // 1
graph.addVertex('B'); // 2
graph.addVertex('C'); // 3
graph.addVertex('D'); // 4
graph.addEdge(0, 1); // S - A
graph.addEdge(0, 2); // S - B
graph.addEdge(0, 3); // S - C
graph.addEdge(1, 4); // A - D
graph.addEdge(2, 4); // B - D
graph.addEdge(3, 4); // C - D
System.out.print("Breadth First Search: ");
graph.breadthFirstSearch();
}
}
Output
Breadth First Search: S A B C D
#Python program for Breadth First Search
# defining MAX 5
MAX = 5
class Vertex:
def __init__(self, label):
self.label = label
self.visited = False
# queue variables
queue = [0] * MAX
rear = -1
front = 0
queueItemCount = 0
# graph variables
#array of vertices
lstVertices = [None] * MAX
#adjacency matrix
adjMatrix = [[0] * MAX for _ in range(MAX)]
#vertex count
vertexCount = 0
# queue functions
def insert(data):
global rear, queueItemCount
rear += 1
queue[rear] = data
queueItemCount += 1
def removeData():
global front, queueItemCount
queueItemCount -= 1
data = queue[front]
front += 1
return data
def isQueueEmpty():
return queueItemCount == 0
# graph functions
#add vertex to the vertex list
def addVertex(label):
global vertexCount
vertex = Vertex(label)
lstVertices[vertexCount] = vertex
vertexCount += 1
#add edge to edge array
def addEdge(start, end):
adjMatrix[start][end] = 1
adjMatrix[end][start] = 1
#Display the vertex
def displayVertex(vertexIndex):
print(lstVertices[vertexIndex].label, end=" ")
#Get the adjacent unvisited vertex
def getAdjUnvisitedVertex(vertexIndex):
for i in range(vertexCount):
if adjMatrix[vertexIndex][i] == 1 and not lstVertices[i].visited:
return i
return -1
def breadthFirstSearch():
#mark first node as visited
lstVertices[0].visited = True
#Display the vertex
displayVertex(0)
#insert vertex index in queue
insert(0)
while not isQueueEmpty():
#get the unvisited vertex of vertex which is at front of the queue
tempVertex = removeData()
#no adjacent vertex found
unvisitedVertex = getAdjUnvisitedVertex(tempVertex)
while unvisitedVertex != -1:
lstVertices[unvisitedVertex].visited = True
displayVertex(unvisitedVertex)
insert(unvisitedVertex)
unvisitedVertex = getAdjUnvisitedVertex(tempVertex)
#queue is empty, search is complete, reset the visited flag
for i in range(vertexCount):
lstVertices[i].visited = False
# main function
if __name__ == "__main__":
#set adjacency
for i in range(MAX):
#matrix to 0
for j in range(MAX):
adjMatrix[i][j] = 0
addVertex('S')
addVertex('A')
addVertex('B')
addVertex('C')
addVertex('D')
addEdge(0, 1)
addEdge(0, 2)
addEdge(0, 3)
addEdge(1, 4)
addEdge(2, 4)
addEdge(3, 4)
print("Breadth First Search: ", end="")
breadthFirstSearch()
Output
Breadth First Search: S A B C D
Spanning Tree
A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected..
By this definition, we can draw a conclusion that every connected and undirected Graph G has at least one spanning tree. A disconnected graph does not have any spanning tree, as it cannot be spanned to all its vertices.
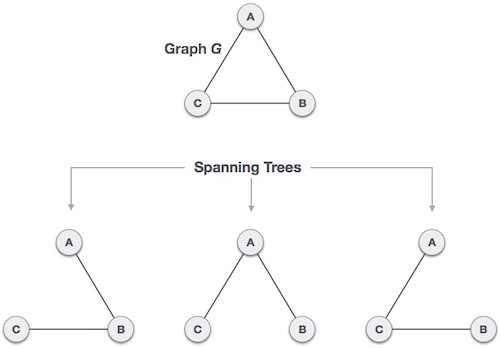
We found three spanning trees off one complete graph. A complete undirected graph can have maximum nn-2 number of spanning trees, where n is the number of nodes. In the above addressed example, n is 3, hence 33−2 = 3 spanning trees are possible.
General Properties of Spanning Tree
We now understand that one graph can have more than one spanning tree. Following are a few properties of the spanning tree connected to graph G −
A connected graph G can have more than one spanning tree.
All possible spanning trees of graph G, have the same number of edges and vertices.
The spanning tree does not have any cycle (loops).
Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected.
Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic.
Mathematical Properties of Spanning Tree
Spanning tree has n-1 edges, where n is the number of nodes (vertices).
From a complete graph, by removing maximum e - n + 1 edges, we can construct a spanning tree.
A complete graph can have maximum nn-2 number of spanning trees.
Thus, we can conclude that spanning trees are a subset of connected Graph G and disconnected graphs do not have spanning tree.
Application of Spanning Tree
Spanning tree is basically used to find a minimum path to connect all nodes in a graph. Common application of spanning trees are −
Civil Network Planning
Computer Network Routing Protocol
Cluster Analysis
Let us understand this through a small example. Consider, city network as a huge graph and now plans to deploy telephone lines in such a way that in minimum lines we can connect to all city nodes. This is where the spanning tree comes into picture.
Minimum Spanning Tree (MST)
In a weighted graph, a minimum spanning tree is a spanning tree that has minimum weight than all other spanning trees of the same graph. In real-world situations, this weight can be measured as distance, congestion, traffic load or any arbitrary value denoted to the edges.
Minimum Spanning-Tree Algorithm
We shall learn about two most important spanning tree algorithms here −
Both are greedy algorithms.
Tree Data Structure
A tree is a non-linear abstract data type with a hierarchy-based structure. It consists of nodes (where the data is stored) that are connected via links. The tree data structure stems from a single node called a root node and has subtrees connected to the root.
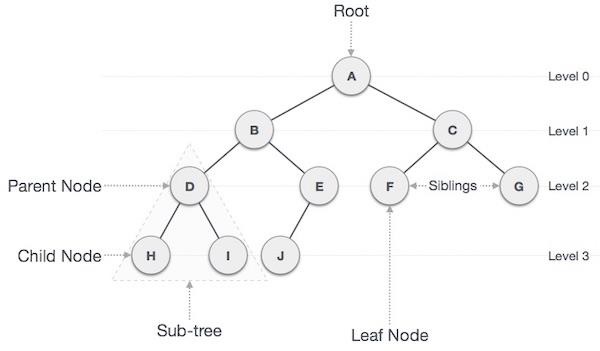
Important Terms
Following are the important terms with respect to tree.
Path − Path refers to the sequence of nodes along the edges of a tree.
Root − The node at the top of the tree is called root. There is only one root per tree and one path from the root node to any node.
Parent − Any node except the root node has one edge upward to a node called parent.
Child − The node below a given node connected by its edge downward is called its child node.
Leaf − The node which does not have any child node is called the leaf node.
Subtree − Subtree represents the descendants of a node.
Visiting − Visiting refers to checking the value of a node when control is on the node.
Traversing − Traversing means passing through nodes in a specific order.
Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
Keys − Key represents a value of a node based on which a search operation is to be carried out for a node.
Types of Trees
There are three types of trees −
General Trees
Binary Trees
Binary Search Trees
General Trees
General trees are unordered tree data structures where the root node has minimum 0 or maximum n subtrees.
The General trees have no constraint placed on their hierarchy. The root node thus acts like the superset of all the other subtrees.
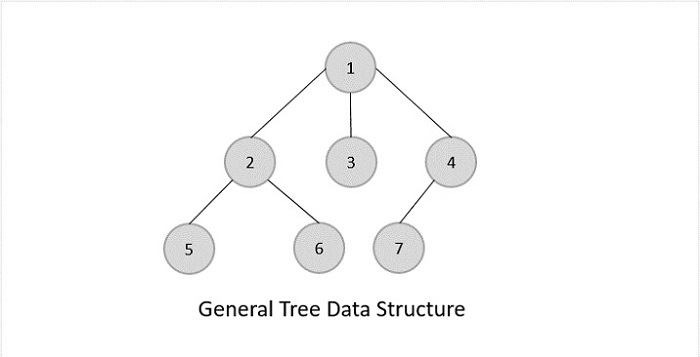
Binary Trees
Binary Trees are general trees in which the root node can only hold up to maximum 2 subtrees: left subtree and right subtree. Based on the number of children, binary trees are divided into three types.
Full Binary Tree
A full binary tree is a binary tree type where every node has either 0 or 2 child nodes.
Complete Binary Tree
A complete binary tree is a binary tree type where all the leaf nodes must be on the same level. However, root and internal nodes in a complete binary tree can either have 0, 1 or 2 child nodes.
Perfect Binary Tree
A perfect binary tree is a binary tree type where all the leaf nodes are on the same level and every node except leaf nodes have 2 children.
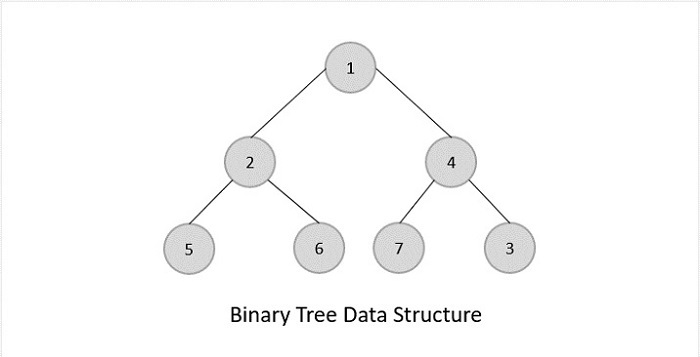
Binary Search Trees
Binary Search Trees possess all the properties of Binary Trees including some extra properties of their own, based on some constraints, making them more efficient than binary trees.
The data in the Binary Search Trees (BST) is always stored in such a way that the values in the left subtree are always less than the values in the root node and the values in the right subtree are always greater than the values in the root node, i.e. left subtree < root node right subtree.
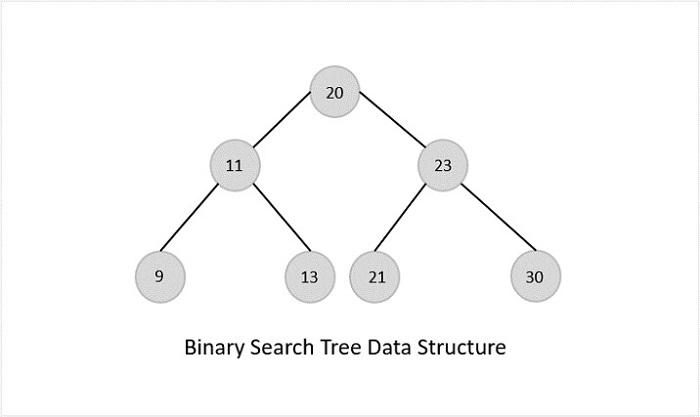
Advantages of BST
Binary Search Trees are more efficient than Binary Trees since time complexity for performing various operations reduces.
Since the order of keys is based on just the parent node, searching operation becomes simpler.
The alignment of BST also favors Range Queries, which are executed to find values existing between two keys. This helps in the Database Management System.
Disadvantages of BST
The main disadvantage of Binary Search Trees is that if all elements in nodes are either greater than or lesser than the root node, the tree becomes skewed. Simply put, the tree becomes slanted to one side completely.
This skewness will make the tree a linked list rather than a BST, since the worst case time complexity for searching operation becomes O(n).
To overcome this issue of skewness in the Binary Search Trees, the concept of Balanced Binary Search Trees was introduced.
Balanced Binary Search Trees
Consider a Binary Search Tree with m as the height of the left subtree and n as the height of the right subtree. If the value of (m-n) is equal to 0,1 or -1, the tree is said to be a Balanced Binary Search Tree.
The trees are designed in a way that they self-balance once the height difference exceeds 1. Binary Search Trees use rotations as self-balancing algorithms. There are four different types of rotations: Left Left, Right Right, Left Right, Right Left.
There are various types of self-balancing binary search trees −
AVL Trees
Red Black Trees
B Trees
B+ Trees
Splay Trees
Priority Search Trees
Tree Traversal
Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −
In-order Traversal
Pre-order Traversal
Post-order Traversal
Generally, we traverse a tree to search or locate a given item or key in the tree or to print all the values it contains.
In-order Traversal
In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.
If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.
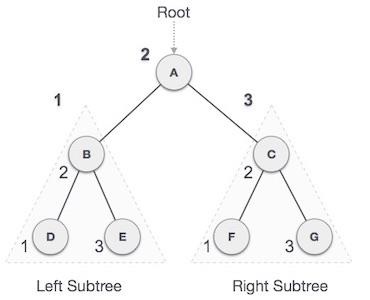
We start from A, and following in-order traversal, we move to its left subtree B.B is also traversed in-order. The process goes on until all the nodes are visited. The output of in-order traversal of this tree will be −
D B E A F C G
Algorithm
Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Visit root node.
Step 3 − Recursively traverse right subtree.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void inorder_traversal(struct node* root){
if(root != NULL) {
inorder_traversal(root->leftChild);
printf("%d ",root->data);
inorder_traversal(root->rightChild);
}
}
int main(){
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
printf("\nInorder traversal: ");
inorder_traversal(root);
return 0;
}
Output
Inorder traversal: 10 14 19 27 31 35 42
#include <iostream>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void inorder_traversal(struct node* root){
if(root != NULL) {
inorder_traversal(root->leftChild);
printf("%d ",root->data);
inorder_traversal(root->rightChild);
}
}
int main(){
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
printf("\nInorder traversal: ");
inorder_traversal(root);
return 0;
}
Output
Inorder traversal: 10 14 19 27 31 35 42
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void inorder_traversal(Node node) {
if(node != null) {
inorder_traversal(node.leftChild);
System.out.print(node.data + " ");
inorder_traversal(node.rightChild);
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(3);
tree.root.leftChild.leftChild = new Node(44);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("\nInorder traversal: ");
tree.inorder_traversal(tree.root);
}
}
Output
Inorder traversal: 44 12 17 27 56 3
class Node:
def __init__(self, key):
self.leftChild = None
self.rightChild = None
self.data = key
# Create a function to perform inorder tree traversal
def InorderTraversal(root):
if root:
InorderTraversal(root.leftChild)
print(root.data)
InorderTraversal(root.rightChild)
# Main class
if __name__ == "__main__":
root = Node(3)
root.leftChild = Node(26)
root.rightChild = Node(42)
root.leftChild.leftChild = Node(54)
root.leftChild.rightChild = Node(65)
root.rightChild.leftChild = Node(12)
# Function call
print("\nInorder traversal of binary tree is")
InorderTraversal(root)
Output
Inorder traversal of binary tree is 54 26 65 3 12 42
Pre-order Traversal
In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.
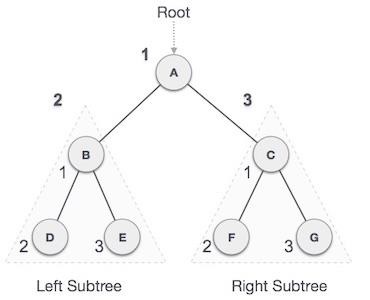
We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of pre-order traversal of this tree will be −
A → B → D → E → C → F → G
Algorithm
Until all nodes are traversed −
Step 1 − Visit root node.
Step 2 − Recursively traverse left subtree.
Step 3 − Recursively traverse right subtree.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void pre_order_traversal(struct node* root){
if(root != NULL) {
printf("%d ",root->data);
pre_order_traversal(root->leftChild);
pre_order_traversal(root->rightChild);
}
}
int main(){
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
printf("\nPreorder traversal: ");
pre_order_traversal(root);
return 0;
}
Output
Preorder traversal: 27 14 10 19 35 31 42
#include <iostream>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void pre_order_traversal(struct node* root){
if(root != NULL) {
printf("%d ",root->data);
pre_order_traversal(root->leftChild);
pre_order_traversal(root->rightChild);
}
}
int main(){
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
printf("\nPreorder traversal: ");
pre_order_traversal(root);
return 0;
}
Output
Preorder traversal: 27 14 10 19 35 31 42
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void pre_order_traversal(Node node) {
if(node != null) {
System.out.print(node.data + " ");
pre_order_traversal(node.leftChild);
pre_order_traversal(node.rightChild);
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(3);
tree.root.leftChild.leftChild = new Node(44);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("\nPreorder traversal: ");
tree.pre_order_traversal(tree.root);
}
}
Output
Preorder traversal: 27 12 44 17 3 56
class Node:
def __init__(self, key):
self.leftChild = None
self.rightChild = None
self.data = key
# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
if root:
print(root.data)
PreorderTraversal(root.leftChild)
PreorderTraversal(root.rightChild)
# Main class
if __name__ == "__main__":
root = Node(3)
root.leftChild = Node(26)
root.rightChild = Node(42)
root.leftChild.leftChild = Node(54)
root.leftChild.rightChild = Node(65)
root.rightChild.leftChild = Node(12)
print("\nPreorder traversal of binary tree is")
PreorderTraversal(root)
Output
Preorder traversal of binary tree is 3 26 54 65 42 12
Post-order Traversal
In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.
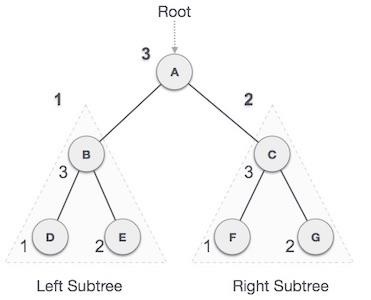
We start from A, and following pre-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of post-order traversal of this tree will be
D → E → B → F → G → C → A
Algorithm
Until all nodes are traversed −
Step 1 − Recursively traverse left subtree.
Step 2 − Recursively traverse right subtree.
Step 3 − Visit root node.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void post_order_traversal(struct node* root){
if(root != NULL) {
post_order_traversal(root->leftChild);
post_order_traversal(root->rightChild);
printf("%d ", root->data);
}
}
int main(){
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
printf("\nPost order traversal: ");
post_order_traversal(root);
return 0;
}
Output
Post order traversal: 10 19 14 31 42 35 27
#include <iostream>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void post_order_traversal(struct node* root){
if(root != NULL) {
post_order_traversal(root->leftChild);
post_order_traversal(root->rightChild);
printf("%d ", root->data);
}
}
int main(){
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
printf("\nPost order traversal: ");
post_order_traversal(root);
return 0;
}
Output
Post order traversal: 10 19 14 31 42 35 27
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void post_order_traversal(Node node) {
if(node != null) {
post_order_traversal(node.leftChild);
post_order_traversal(node.rightChild);
System.out.print(node.data + " ");
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(3);
tree.root.leftChild.leftChild = new Node(44);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("\nPost order traversal: ");
tree.post_order_traversal(tree.root);
}
}
Output
Post order traversal: 44 17 12 56 3 27
class Node:
def __init__(self, key):
self.leftChild = None
self.rightChild = None
self.data = key
# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
if root:
PostorderTraversal(root.leftChild)
PostorderTraversal(root.rightChild)
print(root.data)
# Main class
if __name__ == "__main__":
root = Node(3)
root.leftChild = Node(26)
root.rightChild = Node(42)
root.leftChild.leftChild = Node(54)
root.leftChild.rightChild = Node(65)
root.rightChild.leftChild = Node(12)
print("\nPostorder traversal of binary tree is")
PostorderTraversal(root)
Output
Postorder traversal of binary tree is 54 65 26 12 42 3
To check the C implementation of tree traversing, please click here
Implementation
Traversal is a process to visit all the nodes of a tree and may print their values too. Because, all nodes are connected via edges (links) we always start from the root (head) node. That is, we cannot randomly access a node in a tree. There are three ways which we use to traverse a tree −
In-order Traversal
Pre-order Traversal
Post-order Traversal
We shall now see the implementation of tree traversal in C programming language here using the following binary tree −
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void pre_order_traversal(struct node* root){
if(root != NULL) {
printf("%d ",root->data);
pre_order_traversal(root->leftChild);
pre_order_traversal(root->rightChild);
}
}
void inorder_traversal(struct node* root){
if(root != NULL) {
inorder_traversal(root->leftChild);
printf("%d ",root->data);
inorder_traversal(root->rightChild);
}
}
void post_order_traversal(struct node* root){
if(root != NULL) {
post_order_traversal(root->leftChild);
post_order_traversal(root->rightChild);
printf("%d ", root->data);
}
}
int main(){
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
printf("\nPreorder traversal: ");
pre_order_traversal(root);
printf("\nInorder traversal: ");
inorder_traversal(root);
printf("\nPost order traversal: ");
post_order_traversal(root);
return 0;
}
Output
Preorder traversal: 27 14 10 19 35 31 42 Inorder traversal: 10 14 19 27 31 35 42 Post order traversal: 10 19 14 31 42 35 27
#include <iostream>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void pre_order_traversal(struct node* root){
if(root != NULL) {
printf("%d ",root->data);
pre_order_traversal(root->leftChild);
pre_order_traversal(root->rightChild);
}
}
void inorder_traversal(struct node* root){
if(root != NULL) {
inorder_traversal(root->leftChild);
printf("%d ",root->data);
inorder_traversal(root->rightChild);
}
}
void post_order_traversal(struct node* root){
if(root != NULL) {
post_order_traversal(root->leftChild);
post_order_traversal(root->rightChild);
printf("%d ", root->data);
}
}
int main(){
int i;
int array[7] = { 27, 14, 35, 10, 19, 31, 42 };
for(i = 0; i < 7; i++)
insert(array[i]);
printf("\nPreorder traversal: ");
pre_order_traversal(root);
printf("\nInorder traversal: ");
inorder_traversal(root);
printf("\nPost order traversal: ");
post_order_traversal(root);
return 0;
}
Output
Preorder traversal: 27 14 10 19 35 31 42 Inorder traversal: 10 14 19 27 31 35 42 Post order traversal: 10 19 14 31 42 35 27
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void inorder_traversal(Node node) {
if(node != null) {
inorder_traversal(node.leftChild);
System.out.print(node.data + " ");
inorder_traversal(node.rightChild);
}
}
void pre_order_traversal(Node node) {
if(node != null) {
System.out.print(node.data + " ");
pre_order_traversal(node.leftChild);
pre_order_traversal(node.rightChild);
}
}
void post_order_traversal(Node node) {
if(node != null) {
post_order_traversal(node.leftChild);
post_order_traversal(node.rightChild);
System.out.print(node.data + " ");
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(3);
tree.root.leftChild.leftChild = new Node(44);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("\nInorder traversal: ");
tree.inorder_traversal(tree.root);
System.out.println("\nPreorder traversal: ");
tree.pre_order_traversal(tree.root);
System.out.println("\nPost order traversal: ");
tree.post_order_traversal(tree.root);
}
}
Output
Inorder traversal: 44 12 17 27 56 3 Preorder traversal: 27 12 44 17 3 56 Post order traversal: 44 17 12 56 3 27
class Node:
def __init__(self, key):
self.leftChild = None
self.rightChild = None
self.data = key
# Create a function to perform inorder tree traversal
def InorderTraversal(root):
if root:
InorderTraversal(root.leftChild)
print(root.data)
InorderTraversal(root.rightChild)
# Create a function to perform preorder tree traversal
def PostorderTraversal(root):
if root:
PostorderTraversal(root.leftChild)
PostorderTraversal(root.rightChild)
print(root.data)
# Create a function to perform postorder tree traversal
def PreorderTraversal(root):
if root:
print(root.data)
PreorderTraversal(root.leftChild)
PreorderTraversal(root.rightChild)
# Main class
if __name__ == "__main__":
root = Node(3)
root.leftChild = Node(26)
root.rightChild = Node(42)
root.leftChild.leftChild = Node(54)
root.leftChild.rightChild = Node(65)
root.rightChild.leftChild = Node(12)
# Function call
print("\nInorder traversal of binary tree is")
InorderTraversal(root)
print("\nPreorder traversal of binary tree is")
PreorderTraversal(root)
print("\nPostorder traversal of binary tree is")
PostorderTraversal(root)
Output
Inorder traversal of binary tree is 54 26 65 3 12 42 Preorder traversal of binary tree is 3 26 54 65 42 12 Postorder traversal of binary tree is 54 65 26 12 42 3
Binary Search Tree
A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −
The left sub-tree of a node has a key less than or equal to its parent node's key.
The right sub-tree of a node has a key greater than or equal to its parent node's key.
Thus, BST divides all its sub-trees into two segments; the left sub-tree and the right sub-tree and can be defined as −
left_subtree (keys) node (key) right_subtree (keys)
Representation
BST is a collection of nodes arranged in a way where they maintain BST properties. Each node has a key and an associated value. While searching, the desired key is compared to the keys in BST and if found, the associated value is retrieved.
Following is a pictorial representation of BST −

We observe that the root node key (27) has all less-valued keys on the left sub-tree and the higher valued keys on the right sub-tree.
Basic Operations
Following are the basic operations of a tree −
Search − Searches an element in a tree.
Insert − Inserts an element in a tree.
Pre-order Traversal − Traverses a tree in a pre-order manner.
In-order Traversal − Traverses a tree in an in-order manner.
Post-order Traversal − Traverses a tree in a post-order manner.
Defining a Node
Define a node that stores some data, and references to its left and right child nodes.
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
Search Operation
Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.
Algorithm
1. START 2. Check whether the tree is empty or not 3. If the tree is empty, search is not possible 4. Otherwise, first search the root of the tree. 5. If the key does not match with the value in the root, search its subtrees. 6. If the value of the key is less than the root value, search the left subtree 7. If the value of the key is greater than the root value, search the right subtree. 8. If the key is not found in the tree, return unsuccessful search. 9. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
printf("\nVisiting elements: ");
while(current->data != data) {
if(current != NULL) {
printf("%d ",current->data);
//go to left tree
if(current->data > data) {
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
}
}
return current;
}
void printTree(struct node* Node){
if(Node == NULL)
return;
printTree(Node->leftChild);
printf(" --%d", Node->data);
printTree(Node->rightChild);
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done\n");
printTree(root);
struct node* k;
k = search(35);
if(k != NULL)
printf("\nElement %d found", k->data);
else
printf("\nElement not found");
return 0;
}
Output
Insertion done --15 --20 --35 --50 --55 --65 --90 Visiting elements: 55 20 50 Element 35 found
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
printf("\nVisiting elements: ");
while(current->data != data) {
if(current != NULL) {
printf("%d ",current->data);
//go to left tree
if(current->data > data) {
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
}
}
return current;
}
void printTree(struct node* Node){
if(Node == NULL)
return;
printTree(Node->leftChild);
printf(" --%d", Node->data);
printTree(Node->rightChild);
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done\n");
printTree(root);
struct node* k;
k = search(35);
if(k != NULL)
printf("\nElement %d found", k->data);
else
printf("\nElement not found");
return 0;
}
Output
Insertion done --15 --20 --35 --50 --55 --65 --90 Visiting elements: 55 20 50 Element 35 found
import java.util.Scanner;
class BSTNode {
BSTNode left, right;
int data;
public BSTNode(int n) {
left = null;
right = null;
data = n;
}
}
public class BST {
static BSTNode root;
public BST() {
root = null;
}
private BSTNode insert(BSTNode node, int data) {
if(node == null)
node = new BSTNode(data);
else {
if(data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
}
return node;
}
private boolean search(BSTNode r, int val) {
boolean found = false;
while ((r != null) && !found) {
int rval = r.data;
if(val < rval)
r = r.left;
else if (val > rval)
r = r.right;
else {
found = true;
break;
}
found = search(r, val);
}
return found;
}
void printTree(BSTNode node, String prefix) {
if(node == null)
return;
printTree(node.left , " " + prefix);
System.out.println(prefix + "--" + node.data);
printTree(node.right , prefix + " ");
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
BST bst = new BST();
root = bst.insert(root, 55);
root = bst.insert(root, 20);
root = bst.insert(root, 90);
root = bst.insert(root, 80);
root = bst.insert(root, 50);
root = bst.insert(root, 35);
root = bst.insert(root, 15);
root = bst.insert(root, 65);
bst.printTree(root, " ");
System.out.println("Element found = " + bst.search(root, 80));
}
}
Output
--15
--20--35
--50
--55
--65
--80
--90
Element found = true
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# search method to compare the value with nodes
def search(self, key):
if key < self.data:
if self.left is None:
return str(key)+" Not Found"
return self.left.search(key)
elif key > self.data:
if self.right is None:
return str(key)+" Not Found"
return self.right.search(key)
else:
print(str(self.data) + ' is found')
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print(root.search(17))
print(root.search(12))
Output
17 Not Found 12 is found None
Insert Operation
Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.
Algorithm
1 START 2 If the tree is empty, insert the first element as the root node of the tree. The following elements are added as the leaf nodes. 3 If an element is less than the root value, it is added into the left subtree as a leaf node. 4 If an element is greater than the root value, it is added into the right subtree as a leaf node. 5 The final leaf nodes of the tree point to NULL values as their child nodes. 6 END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void printTree(struct node* Node){
if(Node == NULL)
return;
printTree(Node->leftChild);
printf(" --%d", Node->data);
printTree(Node->rightChild);
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done\n");
printTree(root);
return 0;
}
Output
Insertion done --15 --20 --35 --50 --55 --65 --90
#include <iostream>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
void printTree(struct node* Node){
if(Node == NULL)
return;
printTree(Node->leftChild);
printf(" --%d", Node->data);
printTree(Node->rightChild);
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done\n");
printTree(root);
return 0;
}
Output
Insertion done --15 --20 --35 --50 --55 --65 --90
import java.util.Scanner;
class BSTNode {
BSTNode left, right;
int data;
public BSTNode(int n) {
left = null;
right = null;
data = n;
}
}
public class BST {
static BSTNode root;
public BST() {
root = null;
}
private BSTNode insert(BSTNode node, int data) {
if(node == null)
node = new BSTNode(data);
else {
if(data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
}
return node;
}
void printTree(BSTNode node, String prefix) {
if(node == null)
return;
printTree(node.left , " " + prefix);
System.out.println(prefix + "--" + node.data);
printTree(node.right , prefix + " ");
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
BST bst = new BST();
root = bst.insert(root, 55);
root = bst.insert(root, 20);
root = bst.insert(root, 90);
root = bst.insert(root, 80);
root = bst.insert(root, 50);
root = bst.insert(root, 35);
root = bst.insert(root, 15);
root = bst.insert(root, 65);
bst.printTree(root, " ");
}
}
Output
--15
--20
--35
--50
--55
--65
--80
--90
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Insertion Done")
Output
Insertion Done
Inorder Traversal
The inorder traversal operation in a Binary Search Tree visits all its nodes in the following order −
Firstly, we traverse the left child of the root node/current node, if any.
Next, traverse the current node.
Lastly, traverse the right child of the current node, if any.
Algorithm
1. START 2. Traverse the left subtree, recursively 3. Then, traverse the root node 4. Traverse the right subtree, recursively. 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Inorder Traversal
void inorder(struct node *root){
if (root != NULL) {
inorder(root->left);
printf("%d -> ", root->key);
inorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Inorder traversal: ");
inorder(root);
}
Output
Inorder traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 ->
#include <iostream>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Inorder Traversal
void inorder(struct node *root){
if (root != NULL) {
inorder(root->left);
printf("%d -> ", root->key);
inorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Inorder traversal: ");
inorder(root);
}
Output
Inorder traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 ->
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void inorder_traversal(Node node) {
if(node != null) {
inorder_traversal(node.leftChild);
System.out.print(node.data + " ");
inorder_traversal(node.rightChild);
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(30);
tree.root.leftChild.leftChild = new Node(4);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("\nInorder traversal: ");
tree.inorder_traversal(tree.root);
}
}
Output
Inorder traversal: 4 12 17 27 56 30
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def Inorder(self):
if self.left:
self.left.Inorder()
print(self.data)
if self.right:
self.right.Inorder()
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Inorder Traversal of Binary Search Tree: ")
root.Inorder()
Output
Inorder Traversal of Binary Search Tree: 12 34 54
Preorder Traversal
The preorder traversal operation in a Binary Search Tree visits all its nodes. However, the root node in it is first printed, followed by its left subtree and then its right subtree.
Algorithm
1. START 2. Traverse the root node first. 3. Then traverse the left subtree, recursively 4. Later, traverse the right subtree, recursively. 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Preorder Traversal
void preorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->key);
preorder(root->left);
preorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Preorder traversal: ");
preorder(root);
}
Output
Preorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->
#include <iostream>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Preorder Traversal
void preorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->key);
preorder(root->left);
preorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Preorder traversal: ");
preorder(root);
}
Output
Preorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void preorder_traversal(Node node) {
if(node != null) {
System.out.print(node.data + " ");
preorder_traversal(node.leftChild);
preorder_traversal(node.rightChild);
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(30);
tree.root.leftChild.leftChild = new Node(4);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("\nPreorder traversal: ");
tree.preorder_traversal(tree.root);
}
}
Output
Preorder traversal: 27 12 4 17 30 56
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def Preorder(self):
print(self.data)
if self.left:
self.left.Preorder()
if self.right:
self.right.Preorder()
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Preorder Traversal of Binary Search Tree: ")
root.Preorder()
Output
Preorder Traversal of Binary Search Tree: 54 34 12 5 23 46
Postorder Traversal
Like the other traversals, postorder traversal also visits all the nodes in a Binary Search Tree and displays them. However, the left subtree is printed first, followed by the right subtree and lastly, the root node.
Algorithm
1. START 2. Traverse the left subtree, recursively 3. Traverse the right subtree, recursively. 4. Then, traverse the root node 5. END
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Postorder Traversal
void postorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->key);
postorder(root->left);
postorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Postorder traversal: ");
postorder(root);
}
Output
Postorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 > 65 ->
#include <iostream>
struct node {
int key;
struct node *left, *right;
};
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Postorder Traversal
void postorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->key);
postorder(root->left);
postorder(root->right);
}
}
// Insertion operation
struct node *insert(struct node *node, int key){
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
int main(){
struct node *root = NULL;
root = insert(root, 55);
root = insert(root, 20);
root = insert(root, 90);
root = insert(root, 50);
root = insert(root, 35);
root = insert(root, 15);
root = insert(root, 65);
printf("Postorder traversal: ");
postorder(root);
}
Output
Postorder traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 ->
class Node {
int data;
Node leftChild;
Node rightChild;
public Node(int key) {
data = key;
leftChild = rightChild = null;
}
}
public class TreeDataStructure {
Node root = null;
void postorder_traversal(Node node) {
if(node != null) {
postorder_traversal(node.leftChild);
postorder_traversal(node.rightChild);
System.out.print(node.data + " ");
}
}
public static void main(String args[]) {
TreeDataStructure tree = new TreeDataStructure();
tree.root = new Node(27);
tree.root.leftChild = new Node(12);
tree.root.rightChild = new Node(30);
tree.root.leftChild.leftChild = new Node(4);
tree.root.leftChild.rightChild = new Node(17);
tree.root.rightChild.leftChild = new Node(56);
System.out.println("\nPostorder traversal: ");
tree.postorder_traversal(tree.root);
}
}
Output
Postorder traversal: 4 17 12 56 30 27
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# Print the tree
def Postorder(self):
if self.left:
self.left.Postorder()
if self.right:
self.right.Postorder()
print(self.data)
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Postorder Traversal of Binary Search Tree: ")
root.Postorder()
Output
Postorder Traversal of Binary Search Tree: 5 23 12 46 34 54
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
printf("\n\nVisiting elements: ");
while(current->data != data) {
if(current != NULL) {
printf("%d ",current->data);
//go to left tree
if(current->data > data) {
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
}
}
return current;
}
// Inorder Traversal
void inorder(struct node *root){
if (root != NULL) {
inorder(root->leftChild);
printf("%d -> ", root->data);
inorder(root->rightChild);
}
}
// Preorder Traversal
void preorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->data);
preorder(root->leftChild);
preorder(root->rightChild);
}
}
// Postorder Traversal
void postorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->data);
postorder(root->leftChild);
postorder(root->rightChild);
}
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done\n");
printf("\nPreorder Traversal: ");
preorder(root);
printf("\nInorder Traversal: ");
inorder(root);
printf("\nPostorder Traversal: ");
postorder(root);
struct node* k;
k = search(35);
if(k != NULL)
printf("\nElement %d found", k->data);
else
printf("\nElement not found");
return 0;
}
Output
Insertion done Preorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> Inorder Traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 -> Postorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> Visiting elements: 55 20 50 Element 35 found
#include <iostream>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node *root = NULL;
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->data = item;
temp->leftChild = temp->rightChild = NULL;
return temp;
}
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL) {
root = tempNode;
} else {
current = root;
parent = NULL;
while(1) {
parent = current;
//go to left of the tree
if(data < parent->data) {
current = current->leftChild;
//insert to the left
if(current == NULL) {
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else {
current = current->rightChild;
//insert to the right
if(current == NULL) {
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
printf("\n\nVisiting elements: ");
while(current->data != data) {
if(current != NULL) {
printf("%d ",current->data);
//go to left tree
if(current->data > data) {
current = current->leftChild;
}//else go to right tree
else {
current = current->rightChild;
}
//not found
if(current == NULL) {
return NULL;
}
}
}
return current;
}
// Inorder Traversal
void inorder(struct node *root){
if (root != NULL) {
inorder(root->leftChild);
printf("%d -> ", root->data);
inorder(root->rightChild);
}
}
// Preorder Traversal
void preorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->data);
preorder(root->leftChild);
preorder(root->rightChild);
}
}
// Postorder Traversal
void postorder(struct node *root){
if (root != NULL) {
printf("%d -> ", root->data);
postorder(root->leftChild);
postorder(root->rightChild);
}
}
int main(){
insert(55);
insert(20);
insert(90);
insert(50);
insert(35);
insert(15);
insert(65);
printf("Insertion done\n");
printf("\nPreorder Traversal: ");
preorder(root);
printf("\nInorder Traversal: ");
inorder(root);
printf("\nPostorder Traversal: ");
postorder(root);
struct node* k;
k = search(35);
if(k != NULL)
printf("\nElement %d found", k->data);
else
printf("\nElement not found");
return 0;
}
Output
Insertion done Preorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> Inorder Traversal: 15 -> 20 -> 35 -> 50 -> 55 -> 65 -> 90 -> Postorder Traversal: 55 -> 20 -> 15 -> 50 -> 35 -> 90 -> 65 -> Visiting elements: 55 20 50 Element 35 found
import java.util.Scanner;
class BSTNode {
BSTNode left, right;
int data;
public BSTNode(int n) {
left = null;
right = null;
data = n;
}
}
public class BST {
static BSTNode root;
public BST() {
root = null;
}
public boolean isEmpty() {
return root == null;
}
private BSTNode insert(BSTNode node, int data) {
if(node == null)
node = new BSTNode(data);
else {
if(data <= node.data)
node.left = insert(node.left, data);
else
node.right = insert(node.right, data);
}
return node;
}
public void delete(int k) {
if(isEmpty ())
System.out.println("TREE EMPTY");
else if(search (k) == false)
System.out.println("SORRY " + k + " IS NOT PRESENT");
else {
root=delete(root,k);
System.out.println(k + " DELETED FROM THE TREE");
}
}
public BSTNode delete(BSTNode root, int k) {
BSTNode p, p2, n;
if(root.data == k) {
BSTNode lt, rt;
lt = root.left;
rt = root.right;
if(lt == null && rt == null) {
return null;
} else if(lt == null) {
p = rt;
return p;
} else if(rt == null) {
p = lt;
return p;
} else {
p2 = rt;
p = rt;
while(p.left != null)
p = p.left;
p.left = lt;
return p2;
}
}
if (k < root.data) {
n = delete(root.left, k);
root.left = n;
} else {
n = delete(root.right, k);
root.right = n;
}
return root;
}
public boolean search(int val) {
return search(root, val);
}
private boolean search(BSTNode r, int val) {
boolean found = false;
while ((r != null) && !found) {
int rval = r.data;
if(val < rval)
r = r.left;
else if (val > rval)
r = r.right;
else {
found = true;
break;
}
found = search(r, val);
}
return found;
}
void printTree(BSTNode node, String prefix) {
if(node == null)
return;
printTree(node.left , " " + prefix);
System.out.println(prefix + "--" + node.data);
printTree(node.right , prefix + " ");
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
BST bst = new BST();
root = bst.insert(root, 55);
root = bst.insert(root, 20);
root = bst.insert(root, 90);
root = bst.insert(root, 80);
root = bst.insert(root, 50);
root = bst.insert(root, 35);
root = bst.insert(root, 15);
root = bst.insert(root, 65);
bst.printTree(root, " ");
bst.delete(55);
System.out.println("Element found = " + bst.search(80));
System.out.println("Is Tree Empty? " + bst.isEmpty());
}
}
Output
--15
--20--35
--50
--55
--65
--80
--90
55 DELETED FROM THE TREE
Element found = true
Is Tree Empty? false
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# Insert method to create nodes
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# search method to compare the value with nodes
def search(self, key):
if key < self.data:
if self.left is None:
return str(key)+" Not Found"
return self.left.search(key)
elif key > self.data:
if self.right is None:
return str(key)+" Not Found"
return self.right.search(key)
else:
print(str(self.data) + ' is found')
# Print the tree
def Inorder(self):
if self.left:
self.left.Inorder()
print(self.data)
if self.right:
self.right.Inorder()
# Print the tree
def Preorder(self):
print(self.data)
if self.left:
self.left.Preorder()
if self.right:
self.right.Preorder()
# Print the tree
def Postorder(self):
if self.left:
self.left.Postorder()
if self.right:
self.right.Postorder()
print(self.data)
root = Node(54)
root.insert(34)
root.insert(46)
root.insert(12)
root.insert(23)
root.insert(5)
print("Preorder Traversal of Binary Search Tree: ")
root.Preorder()
print("Inorder Traversal of Binary Search Tree: ")
root.Inorder()
print("Postorder Traversal of Binary Search Tree: ")
root.Postorder()
print(root.search(17))
print(root.search(12))
Output
Preorder Traversal of Binary Search Tree: 54 34 12 5 23 46 Inorder Traversal of Binary Search Tree: 5 12 23 34 46 54 Postorder Traversal of Binary Search Tree: 5 23 12 46 34 54 17 Not Found 12 is found None
AVL Trees
The first type of self-balancing binary search tree to be invented is the AVL tree. The name AVL tree is coined after its inventor's names − Adelson-Velsky and Landis.
In AVL trees, the difference between the heights of left and right subtrees, known as the Balance Factor, must be at most one. Once the difference exceeds one, the tree automatically executes the balancing algorithm until the difference becomes one again.
BALANCE FACTOR = HEIGHT(LEFT SUBTREE) HEIGHT(RIGHT SUBTREE)
There are usually four cases of rotation in the balancing algorithm of AVL trees: LL, RR, LR, RL.
LL Rotations
LL rotation is performed when the node is inserted into the right subtree leading to an unbalanced tree. This is a single left rotation to make the tree balanced again −
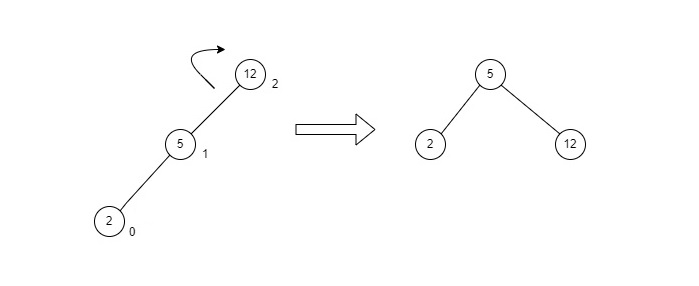
Fig : LL Rotation
The node where the unbalance occurs becomes the left child and the newly added node becomes the right child with the middle node as the parent node.
RR Rotations
RR rotation is performed when the node is inserted into the left subtree leading to an unbalanced tree. This is a single right rotation to make the tree balanced again −
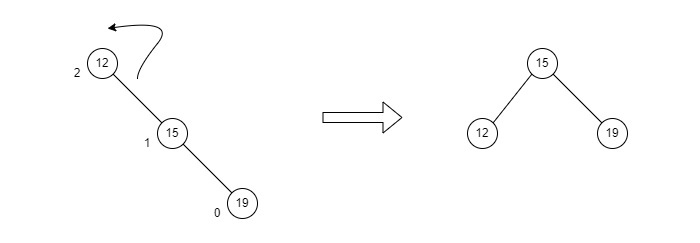
Fig : RR Rotation
The node where the unbalance occurs becomes the right child and the newly added node becomes the left child with the middle node as the parent node.
LR Rotations
LR rotation is the extended version of the previous single rotations, also called a double rotation. It is performed when a node is inserted into the right subtree of the left subtree. The LR rotation is a combination of the left rotation followed by the right rotation. There are multiple steps to be followed to carry this out.
Consider an example with A as the root node, B as the left child of A and C as the right child of B.
Since the unbalance occurs at A, a left rotation is applied on the child nodes of A, i.e. B and C.
After the rotation, the C node becomes the left child of A and B becomes the left child of C.
The unbalance still persists, therefore a right rotation is applied at the root node A and the left child C.
After the final right rotation, C becomes the root node, A becomes the right child and B is the left child.
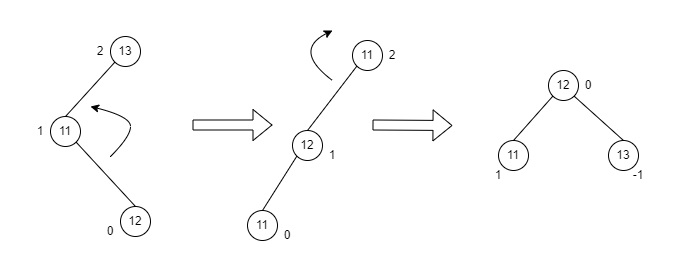
Fig : LR Rotation
RL Rotations
RL rotation is also the extended version of the previous single rotations, hence it is called a double rotation and it is performed if a node is inserted into the left subtree of the right subtree. The RL rotation is a combination of the right rotation followed by the left rotation. There are multiple steps to be followed to carry this out.
Consider an example with A as the root node, B as the right child of A and C as the left child of B.
Since the unbalance occurs at A, a right rotation is applied on the child nodes of A, i.e. B and C.
After the rotation, the C node becomes the right child of A and B becomes the right child of C.
The unbalance still persists, therefore a left rotation is applied at the root node A and the right child C.
After the final left rotation, C becomes the root node, A becomes the left child and B is the right child.
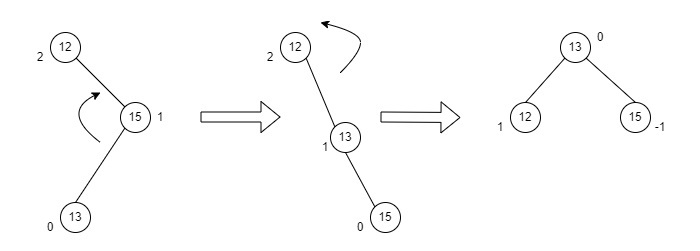
Fig : RL Rotation
Basic Operations of AVL Trees
The basic operations performed on the AVL Tree structures include all the operations performed on a binary search tree, since the AVL Tree at its core is actually just a binary search tree holding all its properties. Therefore, basic operations performed on an AVL Tree are − Insertion and Deletion.
Insertion
The data is inserted into the AVL Tree by following the Binary Search Tree property of insertion, i.e. the left subtree must contain elements less than the root value and right subtree must contain all the greater elements. However, in AVL Trees, after the insertion of each element, the balance factor of the tree is checked; if it does not exceed 1, the tree is left as it is. But if the balance factor exceeds 1, a balancing algorithm is applied to readjust the tree such that balance factor becomes less than or equal to 1 again.
Algorithm
The following steps are involved in performing the insertion operation of an AVL Tree −
Step 1 − Create a node
Step 2 − Check if the tree is empty
Step 3 − If the tree is empty, the new node created will become the root node of the AVL Tree.
Step 4 − If the tree is not empty, we perform the Binary Search Tree insertion operation and check the balancing factor of the node in the tree.
Step 5 − Suppose the balancing factor exceeds 1, we apply suitable rotations on the said node and resume the insertion from Step 4.
START
if node == null then:
return new node
if key < node.key then:
node.left = insert (node.left, key)
else if (key > node.key) then:
node.right = insert (node.right, key)
else
return node
node.height = 1 + max (height (node.left), height (node.right))
balance = getBalance (node)
if balance > 1 and key < node.left.key then:
rightRotate
if balance < -1 and key > node.right.key then:
leftRotate
if balance > 1 and key > node.left.key then:
node.left = leftRotate (node.left)
rightRotate
if balance < -1 and key < node.right.key then:
node.right = rightRotate (node.right)
leftRotate (node)
return node
END
Insertion Example
Let us understand the insertion operation by constructing an example AVL tree with 1 to 7 integers.
Starting with the first element 1, we create a node and measure the balance, i.e., 0.
Since both the binary search property and the balance factor are satisfied, we insert another element into the tree.
The balance factor for the two nodes are calculated and is found to be -1 (Height of left subtree is 0 and height of the right subtree is 1). Since it does not exceed 1, we add another element to the tree.
Now, after adding the third element, the balance factor exceeds 1 and becomes 2. Therefore, rotations are applied. In this case, the RR rotation is applied since the imbalance occurs at two right nodes.
The tree is rearranged as −
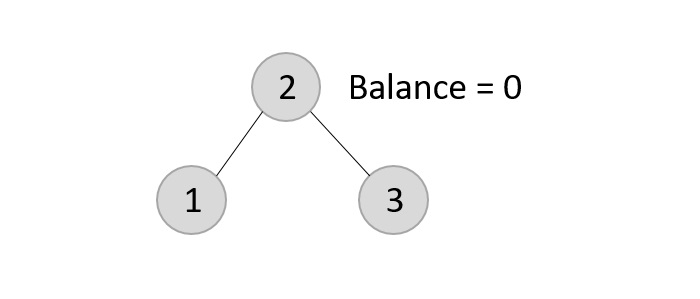
Similarly, the next elements are inserted and rearranged using these rotations. After rearrangement, we achieve the tree as −
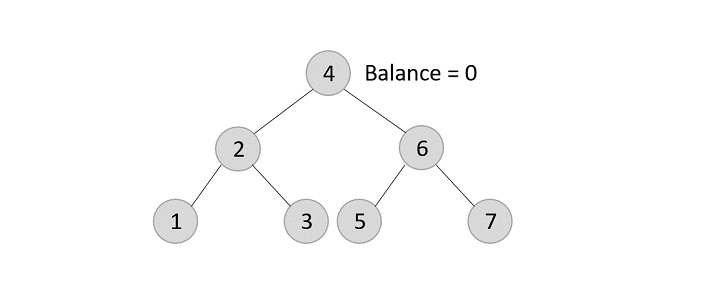
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node *leftChild;
struct Node *rightChild;
int height;
};
int max(int a, int b);
int height(struct Node *N){
if (N == NULL)
return 0;
return N->height;
}
int max(int a, int b){
return (a > b) ? a : b;
}
struct Node *newNode(int data){
struct Node *node = (struct Node *) malloc(sizeof(struct Node));
node->data = data;
node->leftChild = NULL;
node->rightChild = NULL;
node->height = 1;
return (node);
}
struct Node *rightRotate(struct Node *y){
struct Node *x = y->leftChild;
struct Node *T2 = x->rightChild;
x->rightChild = y;
y->leftChild = T2;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
return x;
}
struct Node *leftRotate(struct Node *x){
struct Node *y = x->rightChild;
struct Node *T2 = y->leftChild;
y->leftChild = x;
x->rightChild = T2;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
return y;
}
int getBalance(struct Node *N){
if (N == NULL)
return 0;
return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
if (node == NULL)
return (newNode(data));
if (data < node->data)
node->leftChild = insertNode(node->leftChild, data);
else if (data > node->data)
node->rightChild = insertNode(node->rightChild, data);
else
return node;
node->height = 1 + max(height(node->leftChild),
height(node->rightChild));
int balance = getBalance(node);
if (balance > 1 && data < node->leftChild->data)
return rightRotate(node);
if (balance < -1 && data > node->rightChild->data)
return leftRotate(node);
if (balance > 1 && data > node->leftChild->data) {
node->leftChild = leftRotate(node->leftChild);
return rightRotate(node);
}
if (balance < -1 && data < node->rightChild->data) {
node->rightChild = rightRotate(node->rightChild);
return leftRotate(node);
}
return node;
}
struct Node *minValueNode(struct Node *node){
struct Node *current = node;
while (current->leftChild != NULL)
current = current->leftChild;
return current;
}
void printTree(struct Node *root){
if (root == NULL)
return;
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct Node *root = NULL;
root = insertNode(root, 22);
root = insertNode(root, 14);
root = insertNode(root, 72);
root = insertNode(root, 44);
root = insertNode(root, 25);
root = insertNode(root, 63);
root = insertNode(root, 98);
printf("AVL Tree: ");
printTree(root);
return 0;
}
Output
AVL Tree: 14 22 25 44 63 72 98
#include <iostream>
struct Node {
int data;
struct Node *leftChild;
struct Node *rightChild;
int height;
};
int max(int a, int b);
int height(struct Node *N){
if (N == NULL)
return 0;
return N->height;
}
int max(int a, int b){
return (a > b) ? a : b;
}
struct Node *newNode(int data){
struct Node *node = (struct Node *) malloc(sizeof(struct Node));
node->data = data;
node->leftChild = NULL;
node->rightChild = NULL;
node->height = 1;
return (node);
}
struct Node *rightRotate(struct Node *y){
struct Node *x = y->leftChild;
struct Node *T2 = x->rightChild;
x->rightChild = y;
y->leftChild = T2;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
return x;
}
struct Node *leftRotate(struct Node *x){
struct Node *y = x->rightChild;
struct Node *T2 = y->leftChild;
y->leftChild = x;
x->rightChild = T2;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
return y;
}
int getBalance(struct Node *N){
if (N == NULL)
return 0;
return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
if (node == NULL)
return (newNode(data));
if (data < node->data)
node->leftChild = insertNode(node->leftChild, data);
else if (data > node->data)
node->rightChild = insertNode(node->rightChild, data);
else
return node;
node->height = 1 + max(height(node->leftChild),
height(node->rightChild));
int balance = getBalance(node);
if (balance > 1 && data < node->leftChild->data)
return rightRotate(node);
if (balance < -1 && data > node->rightChild->data)
return leftRotate(node);
if (balance > 1 && data > node->leftChild->data) {
node->leftChild = leftRotate(node->leftChild);
return rightRotate(node);
}
if (balance < -1 && data < node->rightChild->data) {
node->rightChild = rightRotate(node->rightChild);
return leftRotate(node);
}
return node;
}
struct Node *minValueNode(struct Node *node){
struct Node *current = node;
while (current->leftChild != NULL)
current = current->leftChild;
return current;
}
void printTree(struct Node *root){
if (root == NULL)
return;
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->leftChild);
}
}
int main(){
struct Node *root = NULL;
root = insertNode(root, 22);
root = insertNode(root, 14);
root = insertNode(root, 72);
root = insertNode(root, 44);
root = insertNode(root, 25);
root = insertNode(root, 63);
root = insertNode(root, 98);
printf("AVL Tree: ");
printTree(root);
return 0;
}
Output
AVL Tree: 14 22 14 44 14 22 14
import java.util.*;
import java.io.*;
class Node {
int key, height;
Node left, right;
Node (int d) {
key = d;
height = 1;
}
}
public class AVLTree {
Node root;
int height (Node N) {
if (N == null)
return 0;
return N.height;
}
int max (int a, int b) {
return (a > b) ? a : b;
}
Node rightRotate (Node y) {
Node x = y.left;
Node T2 = x.right;
x.right = y;
y.left = T2;
y.height = max (height (y.left), height (y.right)) + 1;
x.height = max (height (x.left), height (x.right)) + 1;
return x;
}
Node leftRotate (Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = max (height (x.left), height (x.right)) + 1;
y.height = max (height (y.left), height (y.right)) + 1;
return y;
}
int getBalance (Node N) {
if (N == null)
return 0;
return height (N.left) - height (N.right);
}
Node insert (Node node, int key) {
if (node == null)
return (new Node (key));
if (key < node.key)
node.left = insert (node.left, key);
else if (key > node.key)
node.right = insert (node.right, key);
else
return node;
node.height = 1 + max (height (node.left), height (node.right));
int balance = getBalance (node);
if (balance > 1 && key < node.left.key)
return rightRotate (node);
if (balance < -1 && key > node.right.key)
return leftRotate (node);
if (balance > 1 && key > node.left.key) {
node.left = leftRotate (node.left);
return rightRotate (node);
}
if (balance < -1 && key < node.right.key) {
node.right = rightRotate (node.right);
return leftRotate (node);
}
return node;
}
void printTree(Node root){
if (root == null)
return;
if (root != null) {
printTree(root.left);
System.out.print(root.key + " ");
printTree(root.left);
}
}
public static void main(String args[]) {
AVLTree tree = new AVLTree();
tree.root = tree.insert(tree.root, 10);
tree.root = tree.insert(tree.root, 11);
tree.root = tree.insert(tree.root, 12);
tree.root = tree.insert(tree.root, 13);
tree.root = tree.insert(tree.root, 14);
tree.root = tree.insert(tree.root, 15);
System.out.println("AVL Tree: ");
tree.printTree(tree.root);
}
}
Output
AVL Tree: 10 11 10 13 10 11 10
class Node(object):
def __init__(self, data):
self.data = data
self.left = None
self.right = None
self.height = 1
class AVLTree(object):
def insert(self, root, key):
if not root:
return Node(key)
elif key < root.data:
root.left = self.insert(root.left, key)
else:
root.right = self.insert(root.right, key)
root.h = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
b = self.getBalance(root)
if b > 1 and key < root.left.data:
return self.rightRotate(root)
if b < -1 and key > root.right.data:
return self.leftRotate(root)
if b > 1 and key > root.left.data:
root.left = self.lefttRotate(root.left)
return self.rightRotate(root)
if b < -1 and key < root.right.data:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def rightRotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def getHeight(self, root):
if not root:
return 0
return root.height
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def Inorder(self, root):
if root.left:
self.Inorder(root.left)
print(root.data)
if root.right:
self.Inorder(root.right)
Tree = AVLTree()
root = None
root = Tree.insert(root, 10)
root = Tree.insert(root, 13)
root = Tree.insert(root, 11)
root = Tree.insert(root, 14)
root = Tree.insert(root, 12)
root = Tree.insert(root, 15)
# Inorder Traversal
print("Inorder traversal of the AVL tree is")
Tree.Inorder(root)
Output
Inorder traversal of the AVL tree is 10 11 12 13 14 15
Deletion
Deletion in the AVL Trees take place in three different scenarios −
Scenario 1 (Deletion of a leaf node) − If the node to be deleted is a leaf node, then it is deleted without any replacement as it does not disturb the binary search tree property. However, the balance factor may get disturbed, so rotations are applied to restore it.
Scenario 2 (Deletion of a node with one child) − If the node to be deleted has one child, replace the value in that node with the value in its child node. Then delete the child node. If the balance factor is disturbed, rotations are applied.
Scenario 3 (Deletion of a node with two child nodes) − If the node to be deleted has two child nodes, find the inorder successor of that node and replace its value with the inorder successor value. Then try to delete the inorder successor node. If the balance factor exceeds 1 after deletion, apply balance algorithms.
START
if root == null: return root
if key < root.key:
root.left = delete Node
else if key > root.key:
root.right = delete Node
else:
if root.left == null or root.right == null then:
Node temp = null
if (temp == root.left)
temp = root.right
else
temp = root.left
if temp == null then:
temp = root
root = null
else
root = temp
else:
temp = minimum valued node
root.key = temp.key
root.right = delete Node
if (root == null) then:
return root
root.height = max (height (root.left), height (root.right)) + 1
balance = getBalance
if balance > 1 and getBalance (root.left) >= 0:
rightRotate
if balance > 1 and getBalance (root.left) < 0:
root.left = leftRotate (root.left);
rightRotate
if balance < -1 and getBalance (root.right) <= 0:
leftRotate
if balance < -1 and getBalance (root.right) > 0:
root.right = rightRotate (root.right);
leftRotate
return root
END
Deletion Example
Using the same tree given above, let us perform deletion in three scenarios −
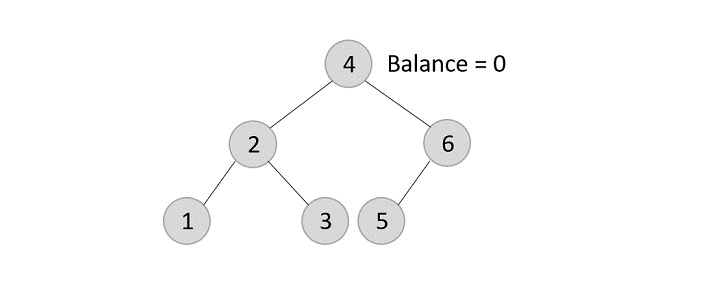
Deleting element 7 from the tree above −
Since the element 7 is a leaf, we normally remove the element without disturbing any other node in the tree
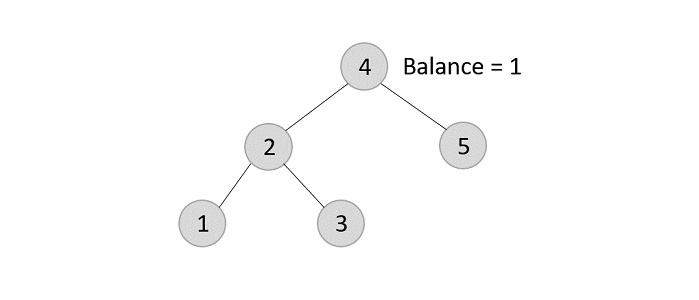
Deleting element 6 from the output tree achieved −
However, element 6 is not a leaf node and has one child node attached to it. In this case, we replace node 6 with its child node: node 5.
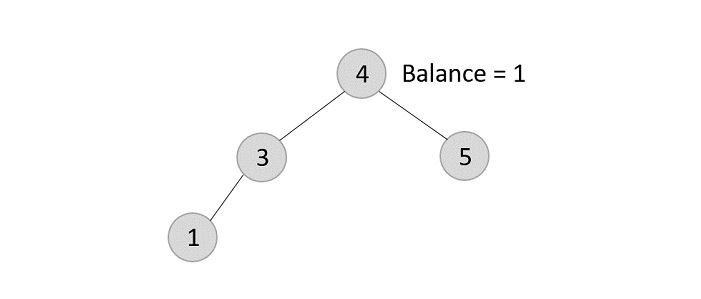
The balance of the tree becomes 1, and since it does not exceed 1 the tree is left as it is. If we delete the element 5 further, we would have to apply the left rotations; either LL or LR since the imbalance occurs at both 1-2-4 and 3-2-4.
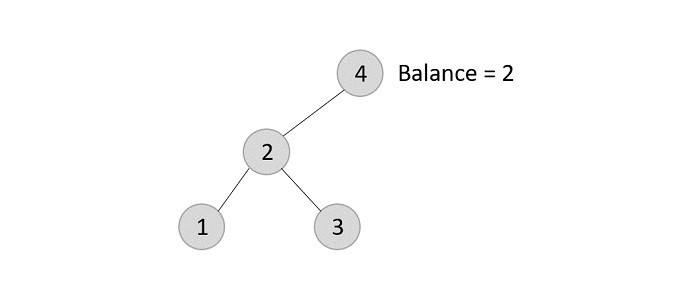
The balance factor is disturbed after deleting the element 5, therefore we apply LL rotation (we can also apply the LR rotation here).
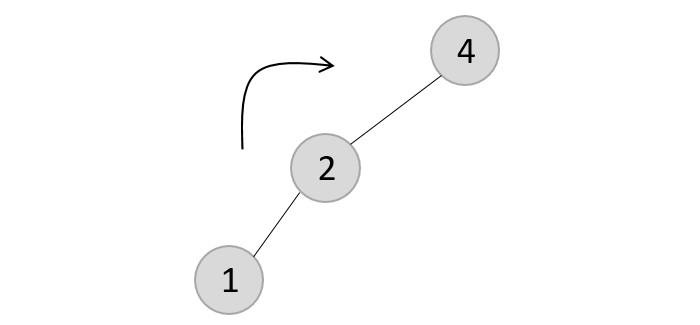
Once the LL rotation is applied on path 1-2-4, the node 3 remains as it was supposed to be the right child of node 2 (which is now occupied by node 4). Hence, the node is added to the right subtree of the node 2 and as the left child of the node 4.
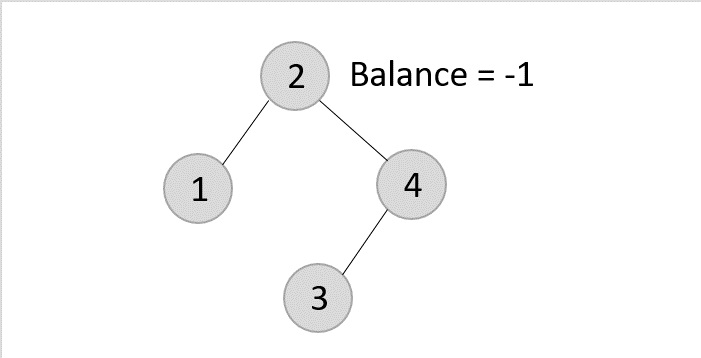
Deleting element 2 from the remaining tree −
As mentioned in scenario 3, this node has two children. Therefore, we find its inorder successor that is a leaf node (say, 3) and replace its value with the inorder successor.
The balance of the tree still remains 1, therefore we leave the tree as it is without performing any rotations.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node *leftChild;
struct Node *rightChild;
int height;
};
int max(int a, int b);
int height(struct Node *N){
if (N == NULL)
return 0;
return N->height;
}
int max(int a, int b){
return (a > b) ? a : b;
}
struct Node *newNode(int data){
struct Node *node = (struct Node *) malloc(sizeof(struct Node));
node->data = data;
node->leftChild = NULL;
node->rightChild = NULL;
node->height = 1;
return (node);
}
struct Node *rightRotate(struct Node *y){
struct Node *x = y->leftChild;
struct Node *T2 = x->rightChild;
x->rightChild = y;
y->leftChild = T2;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
return x;
}
struct Node *leftRotate(struct Node *x){
struct Node *y = x->rightChild;
struct Node *T2 = y->leftChild;
y->leftChild = x;
x->rightChild = T2;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
return y;
}
int getBalance(struct Node *N){
if (N == NULL)
return 0;
return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
if (node == NULL)
return (newNode(data));
if (data < node->data)
node->leftChild = insertNode(node->leftChild, data);
else if (data > node->data)
node->rightChild = insertNode(node->rightChild, data);
else
return node;
node->height = 1 + max(height(node->leftChild),
height(node->rightChild));
int balance = getBalance(node);
if (balance > 1 && data < node->leftChild->data)
return rightRotate(node);
if (balance < -1 && data > node->rightChild->data)
return leftRotate(node);
if (balance > 1 && data > node->leftChild->data) {
node->leftChild = leftRotate(node->leftChild);
return rightRotate(node);
}
if (balance < -1 && data < node->rightChild->data) {
node->rightChild = rightRotate(node->rightChild);
return leftRotate(node);
}
return node;
}
struct Node *minValueNode(struct Node *node){
struct Node *current = node;
while (current->leftChild != NULL)
current = current->leftChild;
return current;
}
struct Node *deleteNode(struct Node *root, int data){
if (root == NULL)
return root;
if (data < root->data)
root->leftChild = deleteNode(root->leftChild, data);
else if (data > root->data)
root->rightChild = deleteNode(root->rightChild, data);
else {
if ((root->leftChild == NULL) || (root->rightChild == NULL)) {
struct Node *temp = root->leftChild ? root->leftChild : root->rightChild;
if (temp == NULL) {
temp = root;
root = NULL;
} else
*root = *temp;
free(temp);
} else {
struct Node *temp = minValueNode(root->rightChild);
root->data = temp->data;
root->rightChild = deleteNode(root->rightChild, temp->data);
}
}
if (root == NULL)
return root;
root->height = 1 + max(height(root->leftChild),
height(root->rightChild));
int balance = getBalance(root);
if (balance > 1 && getBalance(root->leftChild) >= 0)
return rightRotate(root);
if (balance > 1 && getBalance(root->leftChild) < 0) {
root->leftChild = leftRotate(root->leftChild);
return rightRotate(root);
}
if (balance < -1 && getBalance(root->rightChild) <= 0)
return leftRotate(root);
if (balance < -1 && getBalance(root->rightChild) > 0) {
root->rightChild = rightRotate(root->rightChild);
return leftRotate(root);
}
return root;
}
// Print the tree
void printTree(struct Node *root){
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct Node *root = NULL;
root = insertNode(root, 22);
root = insertNode(root, 14);
root = insertNode(root, 72);
root = insertNode(root, 44);
root = insertNode(root, 25);
root = insertNode(root, 63);
root = insertNode(root, 98);
printf("AVL Tree: ");
printTree(root);
root = deleteNode(root, 25);
printf("\nAfter deletion: ");
printTree(root);
return 0;
}
Output
AVL Tree: 14 22 25 44 63 72 98 After deletion: 14 22 44 63 72 98
#include <iostream>
struct Node {
int data;
struct Node *leftChild;
struct Node *rightChild;
int height;
};
int max(int a, int b);
int height(struct Node *N){
if (N == NULL)
return 0;
return N->height;
}
int max(int a, int b){
return (a > b) ? a : b;
}
struct Node *newNode(int data){
struct Node *node = (struct Node *) malloc(sizeof(struct Node));
node->data = data;
node->leftChild = NULL;
node->rightChild = NULL;
node->height = 1;
return (node);
}
struct Node *rightRotate(struct Node *y){
struct Node *x = y->leftChild;
struct Node *T2 = x->rightChild;
x->rightChild = y;
y->leftChild = T2;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
return x;
}
struct Node *leftRotate(struct Node *x){
struct Node *y = x->rightChild;
struct Node *T2 = y->leftChild;
y->leftChild = x;
x->rightChild = T2;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
return y;
}
int getBalance(struct Node *N){
if (N == NULL)
return 0;
return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
if (node == NULL)
return (newNode(data));
if (data < node->data)
node->leftChild = insertNode(node->leftChild, data);
else if (data > node->data)
node->rightChild = insertNode(node->rightChild, data);
else
return node;
node->height = 1 + max(height(node->leftChild),
height(node->rightChild));
int balance = getBalance(node);
if (balance > 1 && data < node->leftChild->data)
return rightRotate(node);
if (balance < -1 && data > node->rightChild->data)
return leftRotate(node);
if (balance > 1 && data > node->leftChild->data) {
node->leftChild = leftRotate(node->leftChild);
return rightRotate(node);
}
if (balance < -1 && data < node->rightChild->data) {
node->rightChild = rightRotate(node->rightChild);
return leftRotate(node);
}
return node;
}
struct Node *minValueNode(struct Node *node){
struct Node *current = node;
while (current->leftChild != NULL)
current = current->leftChild;
return current;
}
struct Node *deleteNode(struct Node *root, int data){
if (root == NULL)
return root;
if (data < root->data)
root->leftChild = deleteNode(root->leftChild, data);
else if (data > root->data)
root->rightChild = deleteNode(root->rightChild, data);
else {
if ((root->leftChild == NULL) || (root->rightChild == NULL)) {
struct Node *temp = root->leftChild ? root->leftChild : root->rightChild;
if (temp == NULL) {
temp = root;
root = NULL;
} else
*root = *temp;
free(temp);
} else {
struct Node *temp = minValueNode(root->rightChild);
root->data = temp->data;
root->rightChild = deleteNode(root->rightChild, temp->data);
}
}
if (root == NULL)
return root;
root->height = 1 + max(height(root->leftChild),
height(root->rightChild));
int balance = getBalance(root);
if (balance > 1 && getBalance(root->leftChild) >= 0)
return rightRotate(root);
if (balance > 1 && getBalance(root->leftChild) < 0) {
root->leftChild = leftRotate(root->leftChild);
return rightRotate(root);
}
if (balance < -1 && getBalance(root->rightChild) <= 0)
return leftRotate(root);
if (balance < -1 && getBalance(root->rightChild) > 0) {
root->rightChild = rightRotate(root->rightChild);
return leftRotate(root);
}
return root;
}
// Print the tree
void printTree(struct Node *root){
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct Node *root = NULL;
root = insertNode(root, 22);
root = insertNode(root, 14);
root = insertNode(root, 72);
root = insertNode(root, 44);
root = insertNode(root, 25);
root = insertNode(root, 63);
root = insertNode(root, 98);
printf("AVL Tree: ");
printTree(root);
root = deleteNode(root, 25);
printf("\nAfter deletion: ");
printTree(root);
return 0;
}
Output
AVL Tree: 14 22 25 44 63 72 98 After deletion: 14 22 44 63 72 98
import java.util.*;
import java.io.*;
class Node {
int key, height;
Node left, right;
Node (int d) {
key = d;
height = 1;
}
}
public class AVLTree {
Node root;
int height (Node N) {
if (N == null)
return 0;
return N.height;
}
int max (int a, int b) {
return (a > b) ? a : b;
}
Node rightRotate (Node y) {
Node x = y.left;
Node T2 = x.right;
x.right = y;
y.left = T2;
y.height = max (height (y.left), height (y.right)) + 1;
x.height = max (height (x.left), height (x.right)) + 1;
return x;
}
Node leftRotate (Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = max (height (x.left), height (x.right)) + 1;
y.height = max (height (y.left), height (y.right)) + 1;
return y;
}
int getBalance (Node N) {
if (N == null)
return 0;
return height (N.left) - height (N.right);
}
Node minValueNode (Node node) {
Node current = node;
while (current.left != null)
current = current.left;
return current;
}
Node deleteNode (Node root, int key) {
if (root == null)
return root;
if (key < root.key)
root.left = deleteNode (root.left, key);
else if (key > root.key)
root.right = deleteNode (root.right, key);
else {
if ((root.left == null) || (root.right == null)) {
Node temp = null;
if (temp == root.left)
temp = root.right;
else
temp = root.left;
if (temp == null) {
temp = root;
root = null;
} else
root = temp;
} else {
Node temp = minValueNode (root.right);
root.key = temp.key;
root.right = deleteNode (root.right, temp.key);
}
}
if (root == null)
return root;
root.height = max (height (root.left), height (root.right)) + 1;
int balance = getBalance (root);
if (balance > 1 && getBalance (root.left) >= 0)
return rightRotate (root);
if (balance > 1 && getBalance (root.left) < 0) {
root.left = leftRotate (root.left);
return rightRotate (root);
}
if (balance < -1 && getBalance (root.right) <= 0)
return leftRotate (root);
if (balance < -1 && getBalance (root.right) > 0) {
root.right = rightRotate (root.right);
return leftRotate (root);
}
return root;
}
public void printTree(Node root) {
if (root == null) return;
printTree(root.left);
System.out.print(root.key + " ");
printTree(root.right);
}
public static void main (String[]args) {
AVLTree tree = new AVLTree();
tree.root = new Node(13);
tree.root.left = new Node(12);
tree.root.left.left = new Node(11);
tree.root.left.left.left = new Node(10);
tree.root.right = new Node(14);
tree.root.right.right = new Node(15);
System.out.println("The AVL Tree is: ");
tree.printTree(tree.root);
tree.root = tree.deleteNode (tree.root, 10);
System.out.println("\n----------------------------------------------\n");
System.out.println("The AVL Tree after deleting 10 is: ");
tree.printTree(tree.root);
System.out.println ("");
}
}
Output
The AVL Tree is: 10 11 12 13 14 15 ---------------------------------------------- The AVL Tree after deleting 10 is: 11 12 13 14 15
class Node(object):
def __init__(self, data):
self.data = data
self.left = None
self.right = None
self.height = 1
class AVLTree(object):
def insert(self, root, key):
if not root:
return Node(key)
elif key < root.data:
root.left = self.insert(root.left, key)
else:
root.right = self.insert(root.right, key)
root.h = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
b = self.getBalance(root)
if b > 1 and key < root.left.data:
return self.rightRotate(root)
if b < -1 and key > root.right.data:
return self.leftRotate(root)
if b > 1 and key > root.left.data:
root.left = self.lefttRotate(root.left)
return self.rightRotate(root)
if b < -1 and key < root.right.data:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
def delete(self, root, key):
if not root:
return root
elif key < root.data:
root.left = self.delete(root.left, key)
elif key > root.data:
root.right = self.delete(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
temp = self.getMindataueNode(root.right)
root.data = temp.data
root.right = self.delete(root.right, temp.data)
if root is None:
return root
root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right))
balance = self.getBalance(root)
if balance > 1 and self.getBalance(root.left) >= 0:
return self.rightRotate(root)
if balance < -1 and self.getBalance(root.right) <= 0:
return self.leftRotate(root)
if balance > 1 and self.getBalance(root.left) < 0:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balance < -1 and self.getBalance(root.right) > 0:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def rightRotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def getHeight(self, root):
if not root:
return 0
return root.height
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def Inorder(self, root):
if root.left:
self.Inorder(root.left)
print(root.data)
if root.right:
self.Inorder(root.right)
Tree = AVLTree()
root = None
root = Tree.insert(root, 10)
root = Tree.insert(root, 13)
root = Tree.insert(root, 11)
root = Tree.insert(root, 14)
root = Tree.insert(root, 12)
root = Tree.insert(root, 15)
# Inorder Traversal
print("Inorder traversal of the AVL tree is")
Tree.Inorder(root)
root = Tree.delete(root, 14)
print("Inorder traversal of the modified AVL tree is")
Tree.Inorder(root)
Output
Inorder traversal of the AVL tree is 10 11 12 13 14 15 Inorder traversal of the modified AVL tree is 10 11 12 13 15
Implementation of AVL Trees
In the following implementation, we consider the inputs in ascending order and store them in AVL Trees by calculating the balance factor and applying rotations.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct Node {
int data;
struct Node *leftChild;
struct Node *rightChild;
int height;
};
int max(int a, int b);
int height(struct Node *N){
if (N == NULL)
return 0;
return N->height;
}
int max(int a, int b){
return (a > b) ? a : b;
}
struct Node *newNode(int data){
struct Node *node = (struct Node *) malloc(sizeof(struct Node));
node->data = data;
node->leftChild = NULL;
node->rightChild = NULL;
node->height = 1;
return (node);
}
struct Node *rightRotate(struct Node *y){
struct Node *x = y->leftChild;
struct Node *T2 = x->rightChild;
x->rightChild = y;
y->leftChild = T2;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
return x;
}
struct Node *leftRotate(struct Node *x){
struct Node *y = x->rightChild;
struct Node *T2 = y->leftChild;
y->leftChild = x;
x->rightChild = T2;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
return y;
}
int getBalance(struct Node *N){
if (N == NULL)
return 0;
return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
if (node == NULL)
return (newNode(data));
if (data < node->data)
node->leftChild = insertNode(node->leftChild, data);
else if (data > node->data)
node->rightChild = insertNode(node->rightChild, data);
else
return node;
node->height = 1 + max(height(node->leftChild),
height(node->rightChild));
int balance = getBalance(node);
if (balance > 1 && data < node->leftChild->data)
return rightRotate(node);
if (balance < -1 && data > node->rightChild->data)
return leftRotate(node);
if (balance > 1 && data > node->leftChild->data) {
node->leftChild = leftRotate(node->leftChild);
return rightRotate(node);
}
if (balance < -1 && data < node->rightChild->data) {
node->rightChild = rightRotate(node->rightChild);
return leftRotate(node);
}
return node;
}
struct Node *minValueNode(struct Node *node){
struct Node *current = node;
while (current->leftChild != NULL)
current = current->leftChild;
return current;
}
struct Node *deleteNode(struct Node *root, int data){
if (root == NULL)
return root;
if (data < root->data)
root->leftChild = deleteNode(root->leftChild, data);
else if (data > root->data)
root->rightChild = deleteNode(root->rightChild, data);
else {
if ((root->leftChild == NULL) || (root->rightChild == NULL)) {
struct Node *temp = root->leftChild ? root->leftChild : root->rightChild;
if (temp == NULL) {
temp = root;
root = NULL;
} else
*root = *temp;
free(temp);
} else {
struct Node *temp = minValueNode(root->rightChild);
root->data = temp->data;
root->rightChild = deleteNode(root->rightChild, temp->data);
}
}
if (root == NULL)
return root;
root->height = 1 + max(height(root->leftChild),
height(root->rightChild));
int balance = getBalance(root);
if (balance > 1 && getBalance(root->leftChild) >= 0)
return rightRotate(root);
if (balance > 1 && getBalance(root->leftChild) < 0) {
root->leftChild = leftRotate(root->leftChild);
return rightRotate(root);
}
if (balance < -1 && getBalance(root->rightChild) <= 0)
return leftRotate(root);
if (balance < -1 && getBalance(root->rightChild) > 0) {
root->rightChild = rightRotate(root->rightChild);
return leftRotate(root);
}
return root;
}
// Print the tree
void printTree(struct Node *root){
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct Node *root = NULL;
root = insertNode(root, 22);
root = insertNode(root, 14);
root = insertNode(root, 72);
root = insertNode(root, 44);
root = insertNode(root, 25);
root = insertNode(root, 63);
root = insertNode(root, 98);
printf("AVL Tree: ");
printTree(root);
root = deleteNode(root, 25);
printf("\nAfter deletion: ");
printTree(root);
return 0;
}
Output
AVL Tree: 14 22 25 44 63 72 98 After deletion: 14 22 44 63 72 98
#include <iostream>
struct Node {
int data;
struct Node *leftChild;
struct Node *rightChild;
int height;
};
int max(int a, int b);
int height(struct Node *N){
if (N == NULL)
return 0;
return N->height;
}
int max(int a, int b){
return (a > b) ? a : b;
}
struct Node *newNode(int data){
struct Node *node = (struct Node *) malloc(sizeof(struct Node));
node->data = data;
node->leftChild = NULL;
node->rightChild = NULL;
node->height = 1;
return (node);
}
struct Node *rightRotate(struct Node *y){
struct Node *x = y->leftChild;
struct Node *T2 = x->rightChild;
x->rightChild = y;
y->leftChild = T2;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
return x;
}
struct Node *leftRotate(struct Node *x){
struct Node *y = x->rightChild;
struct Node *T2 = y->leftChild;
y->leftChild = x;
x->rightChild = T2;
x->height = max(height(x->leftChild), height(x->rightChild)) + 1;
y->height = max(height(y->leftChild), height(y->rightChild)) + 1;
return y;
}
int getBalance(struct Node *N){
if (N == NULL)
return 0;
return height(N->leftChild) - height(N->rightChild);
}
struct Node *insertNode(struct Node *node, int data){
if (node == NULL)
return (newNode(data));
if (data < node->data)
node->leftChild = insertNode(node->leftChild, data);
else if (data > node->data)
node->rightChild = insertNode(node->rightChild, data);
else
return node;
node->height = 1 + max(height(node->leftChild),
height(node->rightChild));
int balance = getBalance(node);
if (balance > 1 && data < node->leftChild->data)
return rightRotate(node);
if (balance < -1 && data > node->rightChild->data)
return leftRotate(node);
if (balance > 1 && data > node->leftChild->data) {
node->leftChild = leftRotate(node->leftChild);
return rightRotate(node);
}
if (balance < -1 && data < node->rightChild->data) {
node->rightChild = rightRotate(node->rightChild);
return leftRotate(node);
}
return node;
}
struct Node *minValueNode(struct Node *node){
struct Node *current = node;
while (current->leftChild != NULL)
current = current->leftChild;
return current;
}
struct Node *deleteNode(struct Node *root, int data){
if (root == NULL)
return root;
if (data < root->data)
root->leftChild = deleteNode(root->leftChild, data);
else if (data > root->data)
root->rightChild = deleteNode(root->rightChild, data);
else {
if ((root->leftChild == NULL) || (root->rightChild == NULL)) {
struct Node *temp = root->leftChild ? root->leftChild : root->rightChild;
if (temp == NULL) {
temp = root;
root = NULL;
} else
*root = *temp;
free(temp);
} else {
struct Node *temp = minValueNode(root->rightChild);
root->data = temp->data;
root->rightChild = deleteNode(root->rightChild, temp->data);
}
}
if (root == NULL)
return root;
root->height = 1 + max(height(root->leftChild),
height(root->rightChild));
int balance = getBalance(root);
if (balance > 1 && getBalance(root->leftChild) >= 0)
return rightRotate(root);
if (balance > 1 && getBalance(root->leftChild) < 0) {
root->leftChild = leftRotate(root->leftChild);
return rightRotate(root);
}
if (balance < -1 && getBalance(root->rightChild) <= 0)
return leftRotate(root);
if (balance < -1 && getBalance(root->rightChild) > 0) {
root->rightChild = rightRotate(root->rightChild);
return leftRotate(root);
}
return root;
}
// Print the tree
void printTree(struct Node *root){
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct Node *root = NULL;
root = insertNode(root, 22);
root = insertNode(root, 14);
root = insertNode(root, 72);
root = insertNode(root, 44);
root = insertNode(root, 25);
root = insertNode(root, 63);
root = insertNode(root, 98);
printf("AVL Tree: ");
printTree(root);
root = deleteNode(root, 25);
printf("\nAfter deletion: ");
printTree(root);
return 0;
}
Output
AVL Tree: 14 22 25 44 63 72 98 After deletion: 14 22 44 63 72 98
import java.util.*;
import java.io.*;
class Node {
int key, height;
Node left, right;
Node (int d) {
key = d;
height = 1;
}
}
public class AVLTree {
Node root;
int height (Node N) {
if (N == null)
return 0;
return N.height;
}
int max (int a, int b) {
return (a > b) ? a : b;
}
Node rightRotate (Node y) {
Node x = y.left;
Node T2 = x.right;
x.right = y;
y.left = T2;
y.height = max (height (y.left), height (y.right)) + 1;
x.height = max (height (x.left), height (x.right)) + 1;
return x;
}
Node leftRotate (Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = max (height (x.left), height (x.right)) + 1;
y.height = max (height (y.left), height (y.right)) + 1;
return y;
}
int getBalance (Node N) {
if (N == null)
return 0;
return height (N.left) - height (N.right);
}
Node insert (Node node, int key) {
if (node == null)
return (new Node (key));
if (key < node.key)
node.left = insert (node.left, key);
else if (key > node.key)
node.right = insert (node.right, key);
else
return node;
node.height = 1 + max (height (node.left), height (node.right));
int balance = getBalance (node);
if (balance > 1 && key < node.left.key)
return rightRotate (node);
if (balance < -1 && key > node.right.key)
return leftRotate (node);
if (balance > 1 && key > node.left.key) {
node.left = leftRotate (node.left);
return rightRotate (node);
}
if (balance < -1 && key < node.right.key) {
node.right = rightRotate (node.right);
return leftRotate (node);
}
return node;
}
Node minValueNode (Node node) {
Node current = node;
while (current.left != null)
current = current.left;
return current;
}
Node deleteNode (Node root, int key) {
if (root == null)
return root;
if (key < root.key)
root.left = deleteNode (root.left, key);
else if (key > root.key)
root.right = deleteNode (root.right, key);
else {
if ((root.left == null) || (root.right == null)) {
Node temp = null;
if (temp == root.left)
temp = root.right;
else
temp = root.left;
if (temp == null) {
temp = root;
root = null;
} else
root = temp;
} else {
Node temp = minValueNode (root.right);
root.key = temp.key;
root.right = deleteNode (root.right, temp.key);
}
}
if (root == null)
return root;
root.height = max (height (root.left), height (root.right)) + 1;
int balance = getBalance (root);
if (balance > 1 && getBalance (root.left) >= 0)
return rightRotate (root);
if (balance > 1 && getBalance (root.left) < 0) {
root.left = leftRotate (root.left);
return rightRotate (root);
}
if (balance < -1 && getBalance (root.right) <= 0)
return leftRotate (root);
if (balance < -1 && getBalance (root.right) > 0) {
root.right = rightRotate (root.right);
return leftRotate (root);
}
return root;
}
public void printTree(Node root) {
if (root == null) return;
printTree(root.left);
System.out.println(root.key);
printTree(root.right);
}
public static void main (String[]args) {
AVLTree tree = new AVLTree();
tree.root = tree.insert (tree.root, 10);
tree.root = tree.insert (tree.root, 11);
tree.root = tree.insert (tree.root, 12);
tree.root = tree.insert (tree.root, 13);
tree.root = tree.insert (tree.root, 14);
tree.root = tree.insert (tree.root, 15);
System.out.println("The AVL Tree is: ");
tree.printTree(tree.root);
tree.root = tree.deleteNode (tree.root, 10);
System.out.println("\n----------------------------------------------\n");
System.out.println("The AVL Tree after deleting 10 is: ");
tree.printTree(tree.root);
System.out.println ("");
}
}
Output
The AVL Tree is: 10 11 12 13 14 15 ---------------------------------------------- The AVL Tree after deleting 10 is: 11 12 13 14 15
class Node(object):
def __init__(self, data):
self.data = data
self.left = None
self.right = None
self.height = 1
class AVLTree(object):
def insert(self, root, key):
if not root:
return Node(key)
elif key < root.data:
root.left = self.insert(root.left, key)
else:
root.right = self.insert(root.right, key)
root.h = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
b = self.getBalance(root)
if b > 1 and key < root.left.data:
return self.rightRotate(root)
if b < -1 and key > root.right.data:
return self.leftRotate(root)
if b > 1 and key > root.left.data:
root.left = self.lefttRotate(root.left)
return self.rightRotate(root)
if b < -1 and key < root.right.data:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
def delete(self, root, key):
if not root:
return root
elif key < root.data:
root.left = self.delete(root.left, key)
elif key > root.data:
root.right = self.delete(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
temp = self.getMindataueNode(root.right)
root.data = temp.data
root.right = self.delete(root.right, temp.data)
if root is None:
return root
root.height = 1 + max(self.getHeight(root.left), self.getHeight(root.right))
balance = self.getBalance(root)
if balance > 1 and self.getBalance(root.left) >= 0:
return self.rightRotate(root)
if balance < -1 and self.getBalance(root.right) <= 0:
return self.leftRotate(root)
if balance > 1 and self.getBalance(root.left) < 0:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balance < -1 and self.getBalance(root.right) > 0:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def rightRotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
def getHeight(self, root):
if not root:
return 0
return root.height
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def Inorder(self, root):
if root.left:
self.Inorder(root.left)
print(root.data)
if root.right:
self.Inorder(root.right)
Tree = AVLTree()
root = None
root = Tree.insert(root, 10)
root = Tree.insert(root, 13)
root = Tree.insert(root, 11)
root = Tree.insert(root, 14)
root = Tree.insert(root, 12)
root = Tree.insert(root, 15)
# Inorder Traversal
print("Inorder traversal of the AVL tree is")
Tree.Inorder(root)
root = Tree.delete(root, 14)
print("Inorder traversal of the modified AVL tree is")
Tree.Inorder(root)
Output
Inorder traversal of the AVL tree is 10 11 12 13 14 15 Inorder traversal of the modified AVL tree is 10 11 12 13 15
Red Black Trees
Red-Black Trees are another type of the Balanced Binary Search Trees with two coloured nodes: Red and Black. It is a self-balancing binary search tree that makes use of these colours to maintain the balance factor during the insertion and deletion operations. Hence, during the Red-Black Tree operations, the memory uses 1 bit of storage to accommodate the colour information of each node
In Red-Black trees, also known as RB trees, there are different conditions to follow while assigning the colours to the nodes.
The root node is always black in colour.
No two adjacent nodes must be red in colour.
Every path in the tree (from the root node to the leaf node) must have the same amount of black coloured nodes.
Even though AVL trees are more balanced than RB trees, with the balancing algorithm in AVL trees being stricter than that of RB trees, multiple and faster insertion and deletion operations are made more efficient through RB trees.
Fig: RB trees
Basic Operations of Red-Black Trees
The operations on Red-Black Trees include all the basic operations usually performed on a Binary Search Tree. Some of the basic operations of an RB Tree include −
Insertion
Deletion
Search
Insertion operation of a Red-Black tree follows the same insertion algorithm of a binary search tree. The elements are inserted following the binary search property and as an addition, the nodes are color coded as red and black to balance the tree according to the red-black tree properties.
Follow the procedure given below to insert an element into a red-black tree by maintaining both binary search tree and red black tree properties.
Case 1 − Check whether the tree is empty; make the current node as the root and color the node black if it is empty.
Case 2 − But if the tree is not empty, we create a new node and color it red. Here we face two different cases −
If the parent of the new node is a black colored node, we exit the operation and tree is left as it is.
If the parent of this new node is red and the color of the parents sibling is either black or if it does not exist, we apply a suitable rotation and recolor accordingly.
If the parent of this new node is red and color of the parents sibling is red, recolor the parent, the sibling and grandparent nodes to black. The grandparent is recolored only if it is not the root node; if it is the root node recolor only the parent and the sibling.
Insertion Example
Let us construct an RB Tree for the first 7 integer numbers to understand the insertion operation in detail −
The tree is checked to be empty so the first node added is a root and is colored black.

Now, the tree is not empty so we create a new node and add the next integer with color red,
The nodes do not violate the binary search tree and RB tree properties, hence we move ahead to add another node.
The tree is not empty; we create a new red node with the next integer to it. But the parent of the new node is not a black colored node,
The tree right now violates both the binary search tree and RB tree properties; since parents sibling is NULL, we apply a suitable rotation and recolor the nodes.
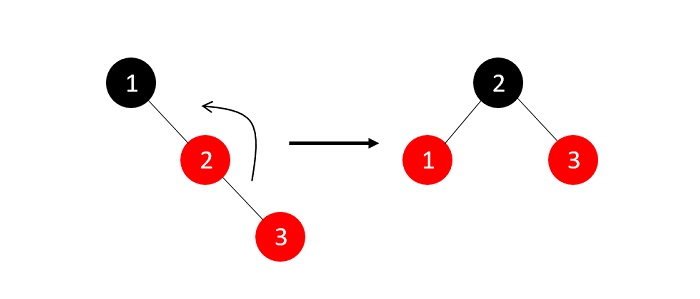
Now that the RB Tree property is restored, we add another node to the tree −
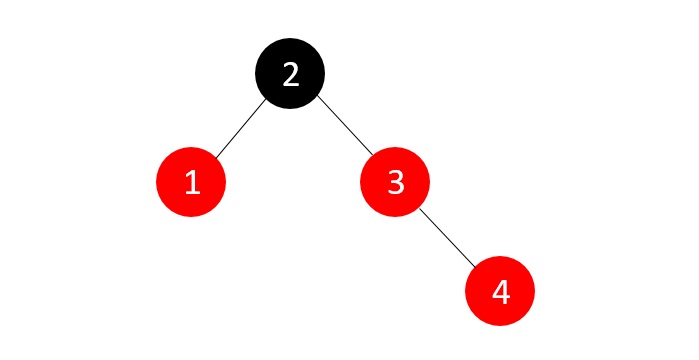
The tree once again violates the RB Tree balance property, so we check for the parents sibling node color, red in this case, so we just recolor the parent and the sibling.
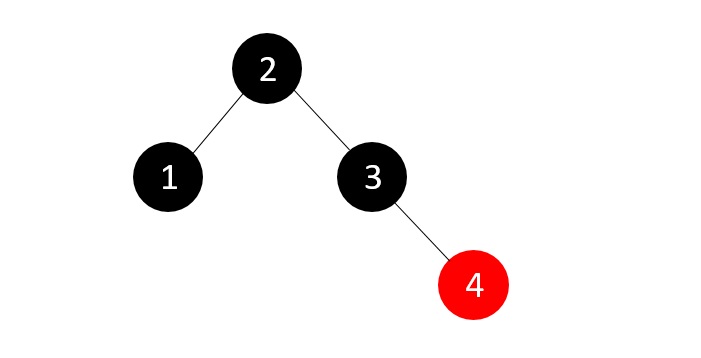
We next insert the element 5, which makes the tree violate the RB Tree balance property once again.
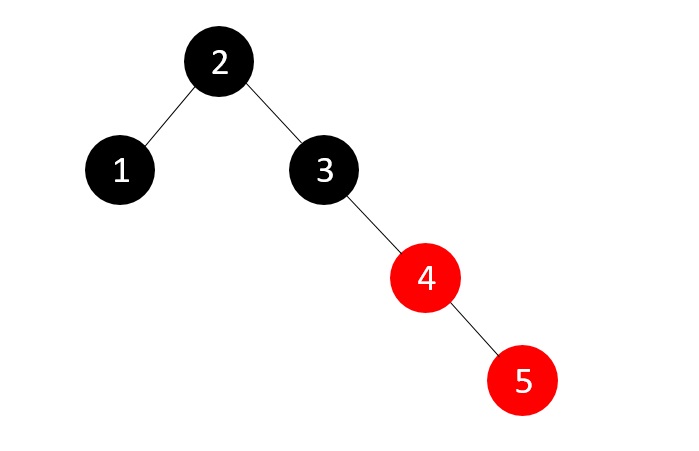
And since the sibling is NULL, we apply suitable rotation and recolor.
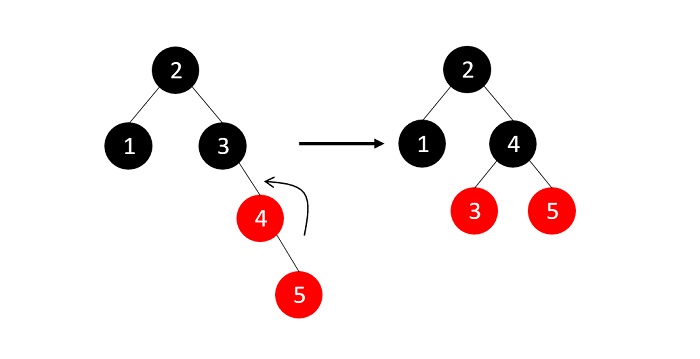
Now, we insert element 6, but the RB Tree property is violated and one of the insertion cases need to be applied −
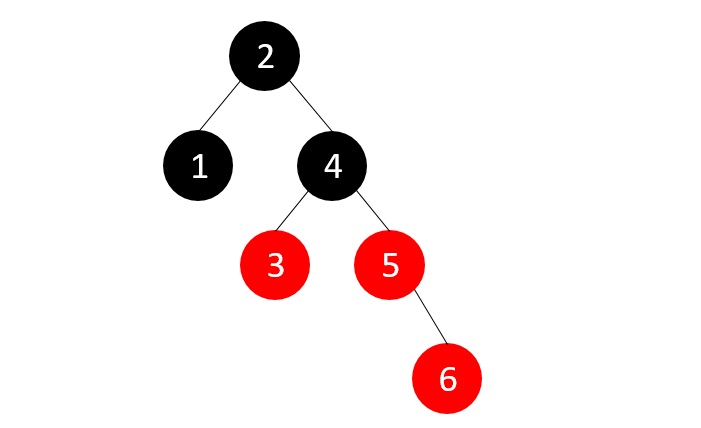
The parents sibling is red, so we recolor the parent, parents sibling and the grandparent nodes since the grandparent is not the root node.
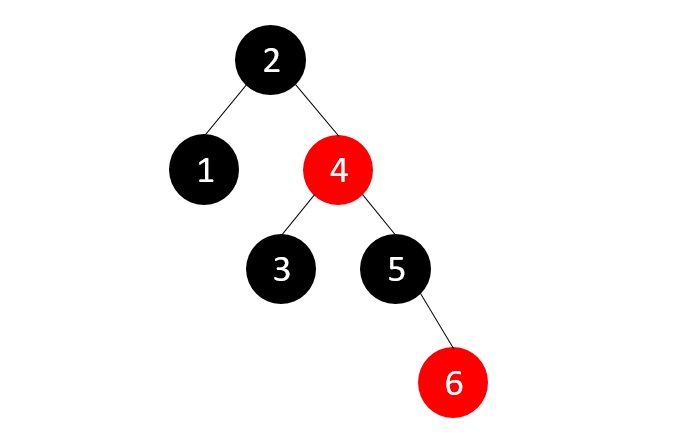
Now, we add the last element, 7, but the parent node of this new node is red.
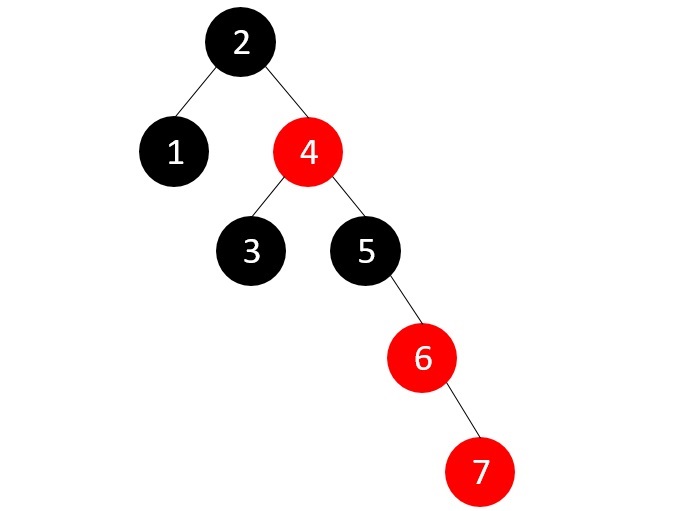
Since the parents sibling is NULL, we apply suitable rotations (RR rotation)
The final RB Tree is achieved.
Deletion
The deletion operation on red black tree must be performed in such a way that it must restore all the properties of a binary search tree and a red black tree. Follow the steps below to perform the deletion operation on the red black tree −
Firstly, we perform deletion based on the binary search tree properties.
Case 1 − If either the node to be deleted or the nodes parent is red, just delete it.
Case 2 − If the node is a double black, just remove the double black (double black occurs when the node to be deleted is a black colored leaf node, as it adds up the NULL nodes which are considered black colored nodes too)
Case 3 − If the double blacks sibling node is also a black node and its child nodes are also black in color, follow the steps below −
Remove double black
Recolor its parent to black (if the parent is a red node, it becomes black; if the parent is already a black node, it becomes double black)
Recolor the parents sibling with red
If double black node still exists, we apply other cases.
Case 4 − If the double black nodes sibling is red, we perform the following steps −
Swap the colors of the parent node and the parents sibling node.
Rotate parent node in the double blacks direction
Reapply other cases that are suitable.
Case 5 − If the double blacks sibling is a black node but the siblings child node that is closest to the double black is red, follows the steps below −
Swap the colors of double blacks sibling and the siblings child in question
Rotate the sibling node is the opposite direction of double black (i.e. if the double black is a right child apply left rotations and vice versa)
Apply case 6.
Case 6 − If the double blacks sibling is a black node but the siblings child node that is farther to the double black is red, follows the steps below −
Swap the colors of double blacks parent and sibling nodes
Rotate the parent in double blacks direction (i.e. if the double black is a right child apply right rotations and vice versa)
Remove double black
Change the color of red child node to black.
Deletion Example
Considering the same constructed Red-Black Tree above, let us delete few elements from the tree.

Delete elements 4, 5, 3 from the tree.
To delete the element 4, let us perform the binary search deletion first.
After performing the binary search deletion, the RB Tree property is not disturbed, therefore the tree is left as it is.
Then, we delete the element 5 using the binary search deletion
But the RB property is violated after performing the binary search deletion, i.e., all the paths in the tree do not hold same number of black nodes; so we swap the colors to balance the tree.
Then, we delete the node 3 from the tree obtained −
Applying binary search deletion, we delete node 3 normally as it is a leaf node. And we get a double node as 3 is a black colored node.
We apply case 3 deletion as double blacks sibling node is black and its child nodes are also black. Here, we remove the double black, recolor the double blacks parent and sibling.
All the desired nodes are deleted and the RB Tree property is maintained.
Search
The search operation in red-black tree follows the same algorithm as that of a binary search tree. The tree is traversed and each node is compared with the key element to be searched; if found it returns a successful search. Otherwise, it returns an unsuccessful search.
Complete implementation
Output
// C++ program for Red black trees algorithmn
#include <iostream>
using namespace std;
struct Node {
int data;
Node *parent;
Node *left;
Node *right;
int color;
};
typedef Node *NodePtr;
class RedBlackTree {
private:
NodePtr root;
NodePtr TNULL;
void initializeNULLNode(NodePtr node, NodePtr parent) {
node->data = 0;
node->parent = parent;
node->left = nullptr;
node->right = nullptr;
node->color = 0;
}
// Preorder
void preOrderHelper(NodePtr node) {
if (node != TNULL) {
cout << node->data << " ";
preOrderHelper(node->left);
preOrderHelper(node->right);
}
}
// Inorder
void inOrderHelper(NodePtr node) {
if (node != TNULL) {
inOrderHelper(node->left);
cout << node->data << " ";
inOrderHelper(node->right);
}
}
// Post order
void postOrderHelper(NodePtr node) {
if (node != TNULL) {
postOrderHelper(node->left);
postOrderHelper(node->right);
cout << node->data << " ";
}
}
NodePtr searchTreeHelper(NodePtr node, int key) {
if (node == TNULL || key == node->data) {
return node;
}
if (key < node->data) {
return searchTreeHelper(node->left, key);
}
return searchTreeHelper(node->right, key);
}
// For balancing the tree after deletion
void deleteFix(NodePtr x) {
NodePtr s;
while (x != root && x->color == 0) {
if (x == x->parent->left) {
s = x->parent->right;
if (s->color == 1) {
s->color = 0;
x->parent->color = 1;
leftRotate(x->parent);
s = x->parent->right;
}
if (s->left->color == 0 && s->right->color == 0) {
s->color = 1;
x = x->parent;
} else {
if (s->right->color == 0) {
s->left->color = 0;
s->color = 1;
rightRotate(s);
s = x->parent->right;
}
s->color = x->parent->color;
x->parent->color = 0;
s->right->color = 0;
leftRotate(x->parent);
x = root;
}
} else {
s = x->parent->left;
if (s->color == 1) {
s->color = 0;
x->parent->color = 1;
rightRotate(x->parent);
s = x->parent->left;
}
if (s->right->color == 0 && s->right->color == 0) {
s->color = 1;
x = x->parent;
} else {
if (s->left->color == 0) {
s->right->color = 0;
s->color = 1;
leftRotate(s);
s = x->parent->left;
}
s->color = x->parent->color;
x->parent->color = 0;
s->left->color = 0;
rightRotate(x->parent);
x = root;
}
}
}
x->color = 0;
}
void rbTransplant(NodePtr u, NodePtr v) {
if (u->parent == nullptr) {
root = v;
} else if (u == u->parent->left) {
u->parent->left = v;
} else {
u->parent->right = v;
}
v->parent = u->parent;
}
void deleteNodeHelper(NodePtr node, int key) {
NodePtr z = TNULL;
NodePtr x, y;
while (node != TNULL) {
if (node->data == key) {
z = node;
}
if (node->data <= key) {
node = node->right;
} else {
node = node->left;
}
}
if (z == TNULL) {
cout << "Key not found in the tree" << endl;
return;
}
y = z;
int y_original_color = y->color;
if (z->left == TNULL) {
x = z->right;
rbTransplant(z, z->right);
} else if (z->right == TNULL) {
x = z->left;
rbTransplant(z, z->left);
} else {
y = minimum(z->right);
y_original_color = y->color;
x = y->right;
if (y->parent == z) {
x->parent = y;
} else {
rbTransplant(y, y->right);
y->right = z->right;
y->right->parent = y;
}
rbTransplant(z, y);
y->left = z->left;
y->left->parent = y;
y->color = z->color;
}
delete z;
if (y_original_color == 0) {
deleteFix(x);
}
}
// For balancing the tree after insertion
void insertFix(NodePtr k) {
NodePtr u;
while (k->parent->color == 1) {
if (k->parent == k->parent->parent->right) {
u = k->parent->parent->left;
if (u->color == 1) {
u->color = 0;
k->parent->color = 0;
k->parent->parent->color = 1;
k = k->parent->parent;
} else {
if (k == k->parent->left) {
k = k->parent;
rightRotate(k);
}
k->parent->color = 0;
k->parent->parent->color = 1;
leftRotate(k->parent->parent);
}
} else {
u = k->parent->parent->right;
if (u->color == 1) {
u->color = 0;
k->parent->color = 0;
k->parent->parent->color = 1;
k = k->parent->parent;
} else {
if (k == k->parent->right) {
k = k->parent;
leftRotate(k);
}
k->parent->color = 0;
k->parent->parent->color = 1;
rightRotate(k->parent->parent);
}
}
if (k == root) {
break;
}
}
root->color = 0;
}
void printHelper(NodePtr root, string indent, bool last) {
if (root != TNULL) {
cout << indent;
if (last) {
cout << "R----";
indent += " ";
} else {
cout << "L----";
indent += "| ";
}
string sColor = root->color ? "RED" : "BLACK";
cout << root->data << "(" << sColor << ")" << endl;
printHelper(root->left, indent, false);
printHelper(root->right, indent, true);
}
}
public:
RedBlackTree() {
TNULL = new Node;
TNULL->color = 0;
TNULL->left = nullptr;
TNULL->right = nullptr;
root = TNULL;
}
void preorder() {
preOrderHelper(this->root);
}
void inorder() {
inOrderHelper(this->root);
}
void postorder() {
postOrderHelper(this->root);
}
NodePtr searchTree(int k) {
return searchTreeHelper(this->root, k);
}
NodePtr minimum(NodePtr node) {
while (node->left != TNULL) {
node = node->left;
}
return node;
}
NodePtr maximum(NodePtr node) {
while (node->right != TNULL) {
node = node->right;
}
return node;
}
NodePtr successor(NodePtr x) {
if (x->right != TNULL) {
return minimum(x->right);
}
NodePtr y = x->parent;
while (y != TNULL && x == y->right) {
x = y;
y = y->parent;
}
return y;
}
NodePtr predecessor(NodePtr x) {
if (x->left != TNULL) {
return maximum(x->left);
}
NodePtr y = x->parent;
while (y != TNULL && x == y->left) {
x = y;
y = y->parent;
}
return y;
}
void leftRotate(NodePtr x) {
NodePtr y = x->right;
x->right = y->left;
if (y->left != TNULL) {
y->left->parent = x;
}
y->parent = x->parent;
if (x->parent == nullptr) {
this->root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
void rightRotate(NodePtr x) {
NodePtr y = x->left;
x->left = y->right;
if (y->right != TNULL) {
y->right->parent = x;
}
y->parent = x->parent;
if (x->parent == nullptr) {
this->root = y;
} else if (x == x->parent->right) {
x->parent->right = y;
} else {
x->parent->left = y;
}
y->right = x;
x->parent = y;
}
// Inserting a node
void insert(int key) {
NodePtr node = new Node;
node->parent = nullptr;
node->data = key;
node->left = TNULL;
node->right = TNULL;
node->color = 1;
NodePtr y = nullptr;
NodePtr x = this->root;
while (x != TNULL) {
y = x;
if (node->data < x->data) {
x = x->left;
} else {
x = x->right;
}
}
node->parent = y;
if (y == nullptr) {
root = node;
} else if (node->data < y->data) {
y->left = node;
} else {
y->right = node;
}
if (node->parent == nullptr) {
node->color = 0;
return;
}
if (node->parent->parent == nullptr) {
return;
}
insertFix(node);
}
NodePtr getRoot() {
return this->root;
}
void deleteNode(int data) {
deleteNodeHelper(this->root, data);
}
void printTree() {
if (root) {
printHelper(this->root, "", true);
}
}
};
int main() {
RedBlackTree V;
V.insert(24);
V.insert(33);
V.insert(42);
V.insert(51);
V.insert(60);
V.insert(40);
V.insert(22);
V.printTree();
cout << endl
<< "After deleting an element" << endl;
V.deleteNode(40);
V.printTree();
}
Output
R----33(BLACK)
L----24(BLACK)
| L----22(RED)
R----51(RED)
L----42(BLACK)
| L----40(RED)
R----60(BLACK)
After deleting an element
R----33(BLACK)
L----24(BLACK)
| L----22(RED)
R----51(RED)
L----42(BLACK)
R----60(BLACK)
// Implementing Red-Black Tree in Java
class Node {
int data;
Node parent;
Node left;
Node right;
int color;
}
public class RedBlackTree {
private Node root;
private Node TNULL;
// Preorder
private void preOrderHelper(Node node) {
if (node != TNULL) {
System.out.print(node.data + " ");
preOrderHelper(node.left);
preOrderHelper(node.right);
}
}
// Inorder
private void inOrderHelper(Node node) {
if (node != TNULL) {
inOrderHelper(node.left);
System.out.print(node.data + " ");
inOrderHelper(node.right);
}
}
// Post order
private void postOrderHelper(Node node) {
if (node != TNULL) {
postOrderHelper(node.left);
postOrderHelper(node.right);
System.out.print(node.data + " ");
}
}
// Search the tree
private Node searchTreeHelper(Node node, int key) {
if (node == TNULL || key == node.data) {
return node;
}
if (key < node.data) {
return searchTreeHelper(node.left, key);
}
return searchTreeHelper(node.right, key);
}
// Balance the tree after deletion of a node
private void fixDelete(Node x) {
Node s;
while (x != root && x.color == 0) {
if (x == x.parent.left) {
s = x.parent.right;
if (s.color == 1) {
s.color = 0;
x.parent.color = 1;
leftRotate(x.parent);
s = x.parent.right;
}
if (s.left.color == 0 && s.right.color == 0) {
s.color = 1;
x = x.parent;
} else {
if (s.right.color == 0) {
s.left.color = 0;
s.color = 1;
rightRotate(s);
s = x.parent.right;
}
s.color = x.parent.color;
x.parent.color = 0;
s.right.color = 0;
leftRotate(x.parent);
x = root;
}
} else {
s = x.parent.left;
if (s.color == 1) {
s.color = 0;
x.parent.color = 1;
rightRotate(x.parent);
s = x.parent.left;
}
if (s.right.color == 0 && s.right.color == 0) {
s.color = 1;
x = x.parent;
} else {
if (s.left.color == 0) {
s.right.color = 0;
s.color = 1;
leftRotate(s);
s = x.parent.left;
}
s.color = x.parent.color;
x.parent.color = 0;
s.left.color = 0;
rightRotate(x.parent);
x = root;
}
}
}
x.color = 0;
}
private void rbTransplant(Node u, Node v) {
if (u.parent == null) {
root = v;
} else if (u == u.parent.left) {
u.parent.left = v;
} else {
u.parent.right = v;
}
v.parent = u.parent;
}
private void deleteNodeHelper(Node node, int key) {
Node z = TNULL;
Node x, y;
while (node != TNULL) {
if (node.data == key) {
z = node;
}
if (node.data <= key) {
node = node.right;
} else {
node = node.left;
}
}
if (z == TNULL) {
System.out.println("Couldn't find key in the tree");
return;
}
y = z;
int yOriginalColor = y.color;
if (z.left == TNULL) {
x = z.right;
rbTransplant(z, z.right);
} else if (z.right == TNULL) {
x = z.left;
rbTransplant(z, z.left);
} else {
y = minimum(z.right);
yOriginalColor = y.color;
x = y.right;
if (y.parent == z) {
x.parent = y;
} else {
rbTransplant(y, y.right);
y.right = z.right;
y.right.parent = y;
}
rbTransplant(z, y);
y.left = z.left;
y.left.parent = y;
y.color = z.color;
}
if (yOriginalColor == 0) {
fixDelete(x);
}
}
// Balance the node after insertion
private void fixInsert(Node k) {
Node u;
while (k.parent.color == 1) {
if (k.parent == k.parent.parent.right) {
u = k.parent.parent.left;
if (u.color == 1) {
u.color = 0;
k.parent.color = 0;
k.parent.parent.color = 1;
k = k.parent.parent;
} else {
if (k == k.parent.left) {
k = k.parent;
rightRotate(k);
}
k.parent.color = 0;
k.parent.parent.color = 1;
leftRotate(k.parent.parent);
}
} else {
u = k.parent.parent.right;
if (u.color == 1) {
u.color = 0;
k.parent.color = 0;
k.parent.parent.color = 1;
k = k.parent.parent;
} else {
if (k == k.parent.right) {
k = k.parent;
leftRotate(k);
}
k.parent.color = 0;
k.parent.parent.color = 1;
rightRotate(k.parent.parent);
}
}
if (k == root) {
break;
}
}
root.color = 0;
}
private void printHelper(Node root, String indent, boolean last) {
if (root != TNULL) {
System.out.print(indent);
if (last) {
System.out.print("R----");
indent += " ";
} else {
System.out.print("L----");
indent += "| ";
}
String sColor = root.color == 1 ? "RED" : "BLACK";
System.out.println(root.data + "(" + sColor + ")");
printHelper(root.left, indent, false);
printHelper(root.right, indent, true);
}
}
public RedBlackTree() {
TNULL = new Node();
TNULL.color = 0;
TNULL.left = null;
TNULL.right = null;
root = TNULL;
}
public void preorder() {
preOrderHelper(this.root);
}
public void inorder() {
inOrderHelper(this.root);
}
public void postorder() {
postOrderHelper(this.root);
}
public Node searchTree(int k) {
return searchTreeHelper(this.root, k);
}
public Node minimum(Node node) {
while (node.left != TNULL) {
node = node.left;
}
return node;
}
public Node maximum(Node node) {
while (node.right != TNULL) {
node = node.right;
}
return node;
}
public Node successor(Node x) {
if (x.right != TNULL) {
return minimum(x.right);
}
Node y = x.parent;
while (y != TNULL && x == y.right) {
x = y;
y = y.parent;
}
return y;
}
public Node predecessor(Node x) {
if (x.left != TNULL) {
return maximum(x.left);
}
Node y = x.parent;
while (y != TNULL && x == y.left) {
x = y;
y = y.parent;
}
return y;
}
public void leftRotate(Node x) {
Node y = x.right;
x.right = y.left;
if (y.left != TNULL) {
y.left.parent = x;
}
y.parent = x.parent;
if (x.parent == null) {
this.root = y;
} else if (x == x.parent.left) {
x.parent.left = y;
} else {
x.parent.right = y;
}
y.left = x;
x.parent = y;
}
public void rightRotate(Node x) {
Node y = x.left;
x.left = y.right;
if (y.right != TNULL) {
y.right.parent = x;
}
y.parent = x.parent;
if (x.parent == null) {
this.root = y;
} else if (x == x.parent.right) {
x.parent.right = y;
} else {
x.parent.left = y;
}
y.right = x;
x.parent = y;
}
public void insert(int key) {
Node node = new Node();
node.parent = null;
node.data = key;
node.left = TNULL;
node.right = TNULL;
node.color = 1;
Node y = null;
Node x = this.root;
while (x != TNULL) {
y = x;
if (node.data < x.data) {
x = x.left;
} else {
x = x.right;
}
}
node.parent = y;
if (y == null) {
root = node;
} else if (node.data < y.data) {
y.left = node;
} else {
y.right = node;
}
if (node.parent == null) {
node.color = 0;
return;
}
if (node.parent.parent == null) {
return;
}
fixInsert(node);
}
public Node getRoot() {
return this.root;
}
public void deleteNode(int data) {
deleteNodeHelper(this.root, data);
}
public void printTree() {
printHelper(this.root, "", true);
}
public static void main(String[] args) {
RedBlackTree V = new RedBlackTree();
V.insert(24);
V.insert(33);
V.insert(42);
V.insert(51);
V.insert(60);
V.insert(40);
V.insert(22);
V.printTree();
System.out.println("\nAfter deleting an element:");
V.deleteNode(40);
V.printTree();
}
}
Output
R----33(BLACK)
L----24(BLACK)
| L----22(RED)
R----51(RED)
L----42(BLACK)
| L----40(RED)
R----60(BLACK)
After deleting an element:
R----33(BLACK)
L----24(BLACK)
| L----22(RED)
R----51(RED)
L----42(BLACK)
R----60(BLACK)
#python program for Red black trees
import sys
# Node creation
class Node():
def __init__(self, item):
self.item = item
self.parent = None
self.left = None
self.right = None
self.color = 1
class RedBlackTree():
def __init__(self):
self.TNULL = Node(0)
self.TNULL.color = 0
self.TNULL.left = None
self.TNULL.right = None
self.root = self.TNULL
# Preorder
def pre_order_helper(self, node):
if node != TNULL:
sys.stdout.write(node.item + " ")
self.pre_order_helper(node.left)
self.pre_order_helper(node.right)
# Inorder
def in_order_helper(self, node):
if node != TNULL:
self.in_order_helper(node.left)
sys.stdout.write(node.item + " ")
self.in_order_helper(node.right)
# Postorder
def post_order_helper(self, node):
if node != TNULL:
self.post_order_helper(node.left)
self.post_order_helper(node.right)
sys.stdout.write(node.item + " ")
# Search the tree
def search_tree_helper(self, node, key):
if node == TNULL or key == node.item:
return node
if key < node.item:
return self.search_tree_helper(node.left, key)
return self.search_tree_helper(node.right, key)
# Balancing the tree after deletion
def delete_fix(self, x):
while x != self.root and x.color == 0:
if x == x.parent.left:
s = x.parent.right
if s.color == 1:
s.color = 0
x.parent.color = 1
self.left_rotate(x.parent)
s = x.parent.right
if s.left.color == 0 and s.right.color == 0:
s.color = 1
x = x.parent
else:
if s.right.color == 0:
s.left.color = 0
s.color = 1
self.right_rotate(s)
s = x.parent.right
s.color = x.parent.color
x.parent.color = 0
s.right.color = 0
self.left_rotate(x.parent)
x = self.root
else:
s = x.parent.left
if s.color == 1:
s.color = 0
x.parent.color = 1
self.right_rotate(x.parent)
s = x.parent.left
if s.right.color == 0 and s.right.color == 0:
s.color = 1
x = x.parent
else:
if s.left.color == 0:
s.right.color = 0
s.color = 1
self.left_rotate(s)
s = x.parent.left
s.color = x.parent.color
x.parent.color = 0
s.left.color = 0
self.right_rotate(x.parent)
x = self.root
x.color = 0
def __rb_transplant(self, u, v):
if u.parent == None:
self.root = v
elif u == u.parent.left:
u.parent.left = v
else:
u.parent.right = v
v.parent = u.parent
# Node deletion
def delete_node_helper(self, node, key):
z = self.TNULL
while node != self.TNULL:
if node.item == key:
z = node
if node.item <= key:
node = node.right
else:
node = node.left
if z == self.TNULL:
print("Cannot find key in the tree")
return
y = z
y_original_color = y.color
if z.left == self.TNULL:
x = z.right
self.__rb_transplant(z, z.right)
elif (z.right == self.TNULL):
x = z.left
self.__rb_transplant(z, z.left)
else:
y = self.minimum(z.right)
y_original_color = y.color
x = y.right
if y.parent == z:
x.parent = y
else:
self.__rb_transplant(y, y.right)
y.right = z.right
y.right.parent = y
self.__rb_transplant(z, y)
y.left = z.left
y.left.parent = y
y.color = z.color
if y_original_color == 0:
self.delete_fix(x)
# Balance the tree after insertion
def fix_insert(self, k):
while k.parent.color == 1:
if k.parent == k.parent.parent.right:
u = k.parent.parent.left
if u.color == 1:
u.color = 0
k.parent.color = 0
k.parent.parent.color = 1
k = k.parent.parent
else:
if k == k.parent.left:
k = k.parent
self.right_rotate(k)
k.parent.color = 0
k.parent.parent.color = 1
self.left_rotate(k.parent.parent)
else:
u = k.parent.parent.right
if u.color == 1:
u.color = 0
k.parent.color = 0
k.parent.parent.color = 1
k = k.parent.parent
else:
if k == k.parent.right:
k = k.parent
self.left_rotate(k)
k.parent.color = 0
k.parent.parent.color = 1
self.right_rotate(k.parent.parent)
if k == self.root:
break
self.root.color = 0
# Printing the tree
def __print_helper(self, node, indent, last):
if node != self.TNULL:
sys.stdout.write(indent)
if last:
sys.stdout.write("R----")
indent += " "
else:
sys.stdout.write("L----")
indent += "| "
s_color = "RED" if node.color == 1 else "BLACK"
print(str(node.item) + "(" + s_color + ")")
self.__print_helper(node.left, indent, False)
self.__print_helper(node.right, indent, True)
def preorder(self):
self.pre_order_helper(self.root)
def inorder(self):
self.in_order_helper(self.root)
def postorder(self):
self.post_order_helper(self.root)
def searchTree(self, k):
return self.search_tree_helper(self.root, k)
def minimum(self, node):
while node.left != self.TNULL:
node = node.left
return node
def maximum(self, node):
while node.right != self.TNULL:
node = node.right
return node
def successor(self, x):
if x.right != self.TNULL:
return self.minimum(x.right)
y = x.parent
while y != self.TNULL and x == y.right:
x = y
y = y.parent
return y
def predecessor(self, x):
if (x.left != self.TNULL):
return self.maximum(x.left)
y = x.parent
while y != self.TNULL and x == y.left:
x = y
y = y.parent
return y
def left_rotate(self, x):
y = x.right
x.right = y.left
if y.left != self.TNULL:
y.left.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.left:
x.parent.left = y
else:
x.parent.right = y
y.left = x
x.parent = y
def right_rotate(self, x):
y = x.left
x.left = y.right
if y.right != self.TNULL:
y.right.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.right:
x.parent.right = y
else:
x.parent.left = y
y.right = x
x.parent = y
def insert(self, key):
node = Node(key)
node.parent = None
node.item = key
node.left = self.TNULL
node.right = self.TNULL
node.color = 1
y = None
x = self.root
while x != self.TNULL:
y = x
if node.item < x.item:
x = x.left
else:
x = x.right
node.parent = y
if y == None:
self.root = node
elif node.item < y.item:
y.left = node
else:
y.right = node
if node.parent == None:
node.color = 0
return
if node.parent.parent == None:
return
self.fix_insert(node)
def get_root(self):
return self.root
def delete_node(self, item):
self.delete_node_helper(self.root, item)
def print_tree(self):
self.__print_helper(self.root, "", True)
if __name__ == "__main__":
V = RedBlackTree()
V.insert(24)
V.insert(33)
V.insert(42)
V.insert(51)
V.insert(60)
V.insert(40)
V.insert(22)
V.print_tree()
print("\nAfter deleting an element")
V.delete_node(40)
V.print_tree()
Output
R----33(BLACK)
L----24(BLACK)
| L----22(RED)
R----51(RED)
L----42(BLACK)
| L----40(RED)
R----60(BLACK)
After deleting an element
R----33(BLACK)
L----24(BLACK)
| L----22(RED)
R----51(RED)
L----42(BLACK)
R----60(BLACK)
B Trees
B trees are extended binary search trees that are specialized in m-way searching, since the order of B trees is m. Order of a tree is defined as the maximum number of children a node can accommodate. Therefore, the height of a b tree is relatively smaller than the height of AVL tree and RB tree.
They are general form of a Binary Search Tree as it holds more than one key and two children.
The various properties of B trees include −
Every node in a B Tree will hold a maximum of m children and (m-1) keys, since the order of the tree is m.
Every node in a B tree, except root and leaf, can hold at least m/2 children
The root node must have no less than two children.
All the paths in a B tree must end at the same level, i.e. the leaf nodes must be at the same level.
A B tree always maintains sorted data.
B trees are also widely used in disk access, minimizing the disk access time since the height of a b tree is low.
Note − A disk access is the memory access to the computer disk where the information is stored and disk access time is the time taken by the system to access the disk memory.
Basic Operations of B Trees
The operations supported in B trees are Insertion, deletion and searching with the time complexity of O(log n) for every operation.
Insertion
The insertion operation for a B Tree is done similar to the Binary Search Tree but the elements are inserted into the same node until the maximum keys are reached. The insertion is done using the following procedure −
Step 1 − Calculate the maximum $\mathrm{\left ( m-1 \right )}$ and minimum $\mathrm{\left ( \left \lceil \frac{m}{2}\right \rceil-1 \right )}$ number of keys a node can hold, where m is denoted by the order of the B Tree.

Step 2 − The data is inserted into the tree using the binary search insertion and once the keys reach the maximum number, the node is split into half and the median key becomes the internal node while the left and right keys become its children.
Step 3 − All the leaf nodes must be on the same level.
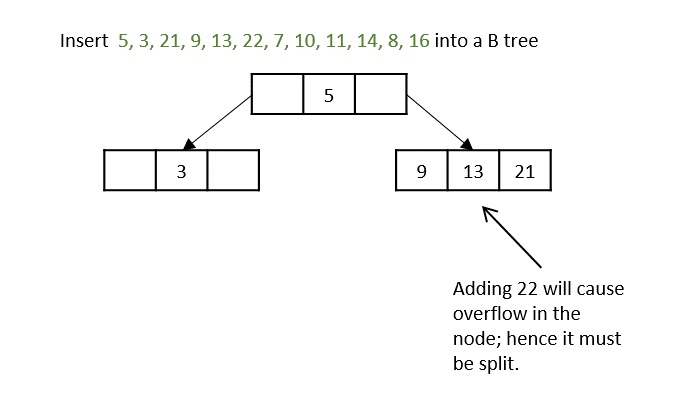
The keys, 5, 3, 21, 9, 13 are all added into the node according to the binary search property but if we add the key 22, it will violate the maximum key property. Hence, the node is split in half, the median key is shifted to the parent node and the insertion is then continued.
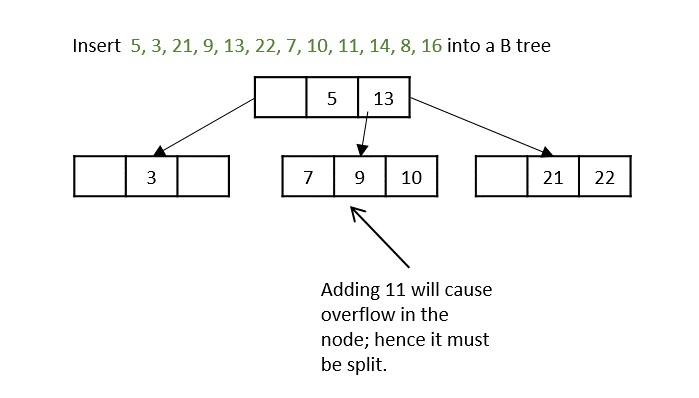
Another hiccup occurs during the insertion of 11, so the node is split and median is shifted to the parent.
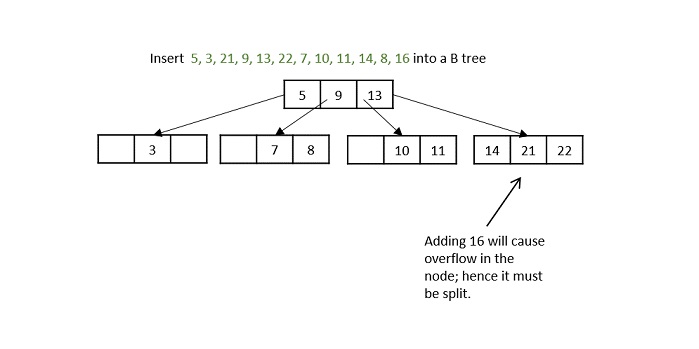
While inserting 16, even if the node is split in two parts, the parent node also overflows as it reached the maximum keys. Hence, the parent node is split first and the median key becomes the root. Then, the leaf node is split in half the median of leaf node is shifted to its parent.
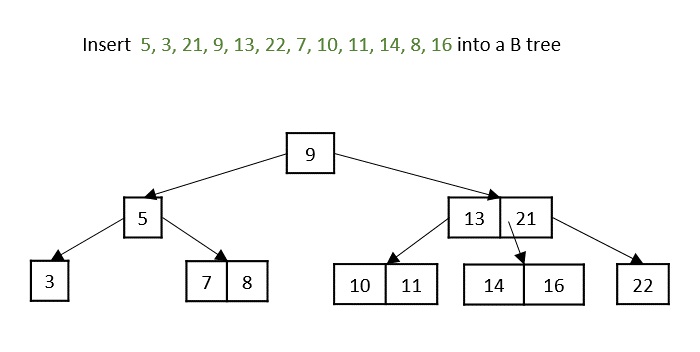
The final B tree after inserting all the elements is achieved.
Example
// Insert the value
void insertion(int item) {
int flag, i;
struct btreeNode *child;
flag = setNodeValue(item, &i, root, &child);
if (flag)
root = createNode(i, child);
}
Deletion
The deletion operation in a B tree is slightly different from the deletion operation of a Binary Search Tree. The procedure to delete a node from a B tree is as follows −
Case 1 − If the key to be deleted is in a leaf node and the deletion does not violate the minimum key property, just delete the node.
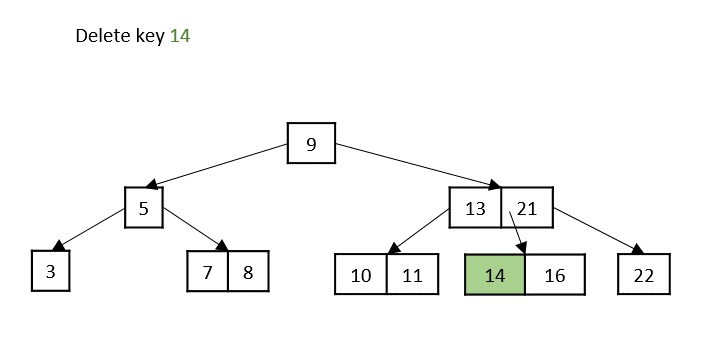
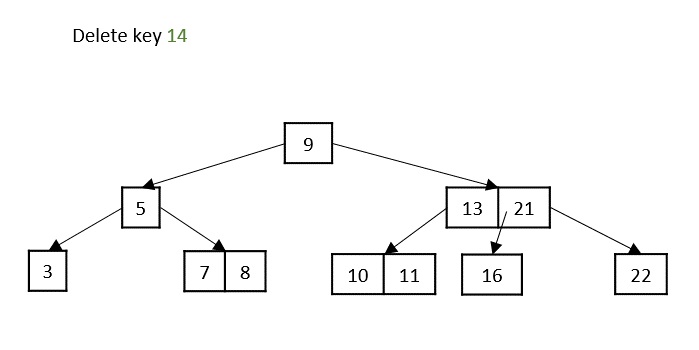
Case 2 − If the key to be deleted is in a leaf node but the deletion violates the minimum key property, borrow a key from either its left sibling or right sibling. In case if both siblings have exact minimum number of keys, merge the node in either of them.
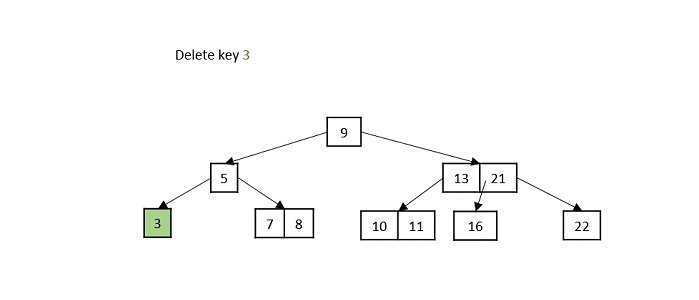
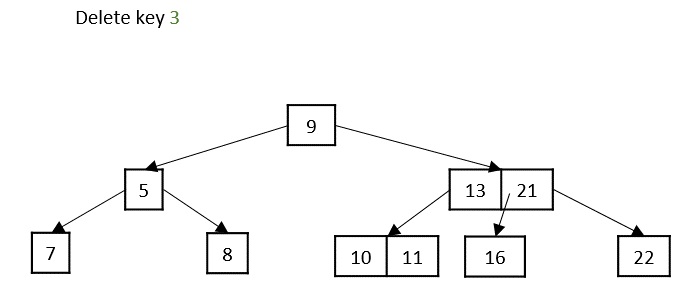
Case 3 − If the key to be deleted is in an internal node, it is replaced by a key in either left child or right child based on which child has more keys. But if both child nodes have minimum number of keys, theyre merged together.
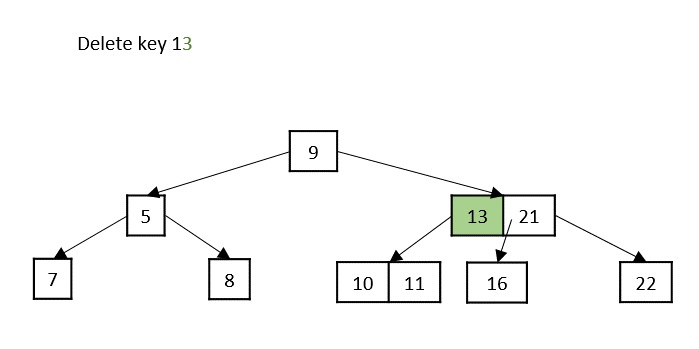
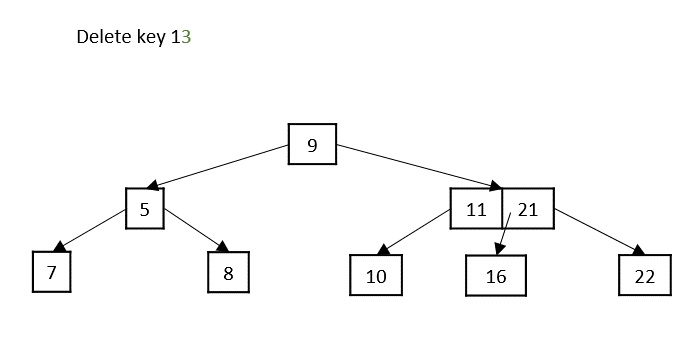
Case 4 − If the key to be deleted is in an internal node violating the minimum keys property, and both its children and sibling have minimum number of keys, merge the children. Then merge its sibling with its parent.
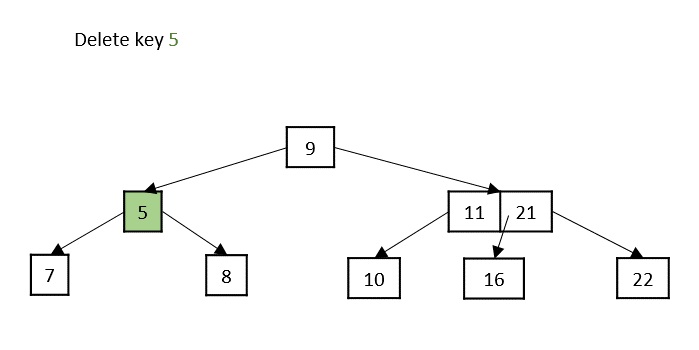
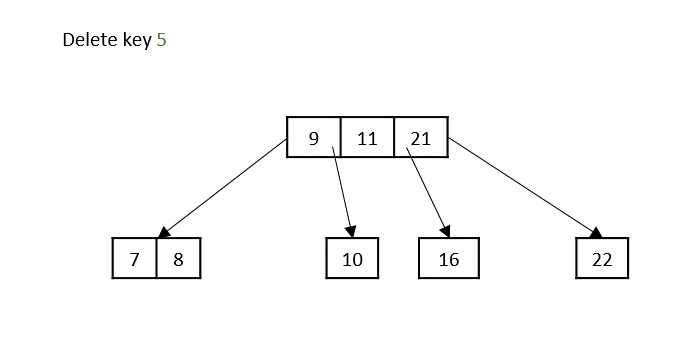
Following is functional C++ code snippet of the deletion operation in B Trees −
// Deletion operation
void deletion(int key){
int index = searchkey(key);
if (index < n && keys[index] == key) {
if (leaf)
deletion_at_leaf(index);
else
deletion_at_nonleaf(index);
} else {
if (leaf) {
cout << "key " << key << " does not exist in the tree\n";
return;
}
bool flag = ((index == n) ? true : false);
if (C[index]->n < t)
fill(index);
if (flag && index > n)
C[index - 1]->deletion(key);
else
C[index]->deletion(key);
}
return;
}
// Deletion at the leaf nodes
void deletion_at_leaf(int index){
for (int i = index + 1; i < n; ++i)
keys[i - 1] = keys[i];
n--;
return;
}
// Deletion at the non leaf node
void deletion_at_nonleaf(int index){
int key = keys[index];
if (C[index]->n >= t) {
int pred = get_Predecessor(index);
keys[index] = pred;
C[index]->deletion(pred);
} else if (C[index + 1]->n >= t) {
int successor = copysuccessoressor(index);
keys[index] = successor;
C[index + 1]->deletion(successor);
} else {
merge(index);
C[index]->deletion(key);
}
return;
}
Example
// C Program for B trees
#include <stdio.h>
#include <stdlib.h>
struct BTree {
//node declaration
int *d;
struct BTree **child_ptr;
int l;
int n;
};
struct BTree *r = NULL;
struct BTree *np = NULL;
struct BTree *x = NULL;
//creation of node
struct BTree* init() {
int i;
np = (struct BTree*)malloc(sizeof(struct BTree));
//order 6
np->d = (int*)malloc(6 * sizeof(int));
np->child_ptr = (struct BTree**)malloc(7 * sizeof(struct BTree*));
np->l = 1;
np->n = 0;
for (i = 0; i < 7; i++) {
np->child_ptr[i] = NULL;
}
return np;
}
//traverse the tree
void traverse(struct BTree *p) {
printf("\n");
int i;
for (i = 0; i < p->n; i++) {
if (p->l == 0) {
traverse(p->child_ptr[i]);
}
printf(" %d", p->d[i]);
}
if (p->l == 0) {
traverse(p->child_ptr[i]);
}
printf("\n");
}
//sort the tree
void sort(int *p, int n) {
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] > p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
int split_child(struct BTree *x, int i) {
int j, mid;
struct BTree *np1, *np3, *y;
np3 = init();
//create new node
np3->l = 1;
if (i == -1) {
mid = x->d[2];
//find mid
x->d[2] = 0;
x->n--;
np1 = init();
np1->l = 0;
x->l = 1;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = x->d[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->d[j] = 0;
x->n--;
}
for (j = 0; j < 6; j++) {
x->child_ptr[j] = NULL;
}
np1->d[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
r = np1;
} else {
y = x->child_ptr[i];
mid = y->d[2];
y->d[2] = 0;
y->n--;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = y->d[j];
np3->n++;
y->d[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insert(int a) {
int i, t;
x = r;
if (x == NULL) {
r = init();
x = r;
} else {
if (x->l == 1 && x->n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < x->n; i++) {
if (a > x->d[i] && a < x->d[i + 1]) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
x = x->child_ptr[i];
} else {
while (x->l == 0) {
for (i = 0; i < x->n; i++) {
if (a > x->d[i] && a < x->d[i + 1]) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
if (x->child_ptr[i]->n == 6) {
t = split_child(x, i);
x->d[x->n] = t;
x->n++;
continue;
} else {
x = x->child_ptr[i];
}
}
}
}
x->d[x->n] = a;
sort(x->d, x->n);
x->n++;
}
int main() {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
printf("B tree:\n");
traverse(r);
return 0;
}
Output
B tree: 10 20 30 40 50
#include<iostream>
using namespace std;
struct BTree {//node declaration
int *d;
BTree **child_ptr;
bool l;
int n;
}*r = NULL, *np = NULL, *x = NULL;
BTree* init() {//creation of node
int i;
np = new BTree;
np->d = new int[6];//order 6
np->child_ptr = new BTree *[7];
np->l = true;
np->n = 0;
for (i = 0; i < 7; i++) {
np->child_ptr[i] = NULL;
}
return np;
}
void traverse(BTree *p) { //traverse the tree
cout<<endl;
int i;
for (i = 0; i < p->n; i++) {
if (p->l == false) {
traverse(p->child_ptr[i]);
}
cout << " " << p->d[i];
}
if (p->l == false) {
traverse(p->child_ptr[i]);
}
cout<<endl;
}
void sort(int *p, int n){ //sort the tree
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] >p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
int split_child(BTree *x, int i) {
int j, mid;
BTree *np1, *np3, *y;
np3 = init();//create new node
np3->l = true;
if (i == -1) {
mid = x->d[2];//find mid
x->d[2] = 0;
x->n--;
np1 = init();
np1->l= false;
x->l= true;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = x->d[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->d[j] = 0;
x->n--;
}
for (j = 0; j < 6; j++) {
x->child_ptr[j] = NULL;
}
np1->d[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
r = np1;
} else {
y = x->child_ptr[i];
mid = y->d[2];
y->d[2] = 0;
y->n--;
for (j = 3; j <6 ; j++) {
np3->d[j - 3] = y->d[j];
np3->n++;
y->d[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insert(int a) {
int i, t;
x = r;
if (x == NULL) {
r = init();
x = r;
} else {
if (x->l== true && x->n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < (x->n); i++) {
if ((a >x->d[i]) && (a < x->d[i + 1])) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
x = x->child_ptr[i];
} else {
while (x->l == false) {
for (i = 0; i < (x->n); i++) {
if ((a >x->d[i]) && (a < x->d[i + 1])) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
if ((x->child_ptr[i])->n == 6) {
t = split_child(x, i);
x->d[x->n] = t;
x->n++;
continue;
} else {
x = x->child_ptr[i];
}
}
}
}
x->d[x->n] = a;
sort(x->d, x->n);
x->n++;
}
int main() {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
cout<<"B tree:\n";
traverse(r);
}
Output
B tree: 10 20 30 40 50
//Java code for B trees
import java.util.Arrays;
class BTree {
private int[] d;
private BTree[] child_ptr;
private boolean l;
private int n;
public BTree() {
d = new int[6]; // order 6
child_ptr = new BTree[7];
l = true;
n = 0;
Arrays.fill(child_ptr, null);
}
public void traverse() {
System.out.println("B tree: ");
for (int i = 0; i < n; i++) {
if (!l) {
child_ptr[i].traverse();
}
System.out.print(d[i] + " ");
}
if (!l) {
child_ptr[n].traverse();
}
System.out.println();
}
public void sort() {
Arrays.sort(d, 0, n);
}
public int splitChild(int i) {
int j, mid;
BTree np1, np3, y;
np3 = new BTree();
np3.l = true;
if (i == -1) {
mid = d[2];
d[2] = 0;
n--;
np1 = new BTree();
np1.l = false;
l = true;
for (j = 3; j < 6; j++) {
np3.d[j - 3] = d[j];
np3.n++;
d[j] = 0;
n--;
}
for (j = 0; j < 6; j++) {
np3.child_ptr[j] = child_ptr[j + 3];
child_ptr[j + 3] = null;
}
np1.d[0] = mid;
np1.child_ptr[0] = this;
np1.child_ptr[1] = np3;
np1.n++;
return mid;
} else {
y = child_ptr[i];
mid = y.d[2];
y.d[2] = 0;
y.n--;
for (j = 3; j < 6; j++) {
np3.d[j - 3] = y.d[j];
np3.n++;
y.d[j] = 0;
y.n--;
}
child_ptr[i + 1] = y;
child_ptr[i + 2] = np3;
return mid;
}
}
public void insert(int a) {
int i, t;
BTree x = this;
if (x.l && x.n == 6) {
t = x.splitChild(-1);
x = this;
for (i = 0; i > x.n; i++) {
if (a > x.d[i] && a < x.d[i + 1]) {
i++;
break;
} else if (a < x.d[0]) {
break;
}
}
x = x.child_ptr[i];
} else {
while (!x.l) {
for (i = 0; i < x.n; i++) {
if (a > x.d[i] && a < x.d[i + 1]) {
i++;
break;
} else if (a < x.d[0]) {
break;
}
}
if (x.child_ptr[i].n == 6) {
t = x.splitChild(i);
x.d[x.n] = t;
x.n++;
continue;
}
x = x.child_ptr[i];
}
}
x.d[x.n] = a;
x.sort();
x.n++;
}
}
public class Main {
public static void main(String[] args) {
BTree bTree = new BTree();
bTree.insert(20);
bTree.insert(10);
bTree.insert(40);
bTree.insert(30);
bTree.insert(50); // Duplicate value, ignored
//call the traverse method
bTree.traverse();
}
}
Output
B tree: 10 20 30 40 50
#python program for B treesa
class BTree:
def __init__(self):
#node declartion
self.d = [0] * 6
self.child_ptr = [None] * 7
self.l = True
self.n = 0
#creation of node
def init():
np = BTree()
np.l = True
np.n = 0
return np
#traverse the tree
def traverse(p):
if p is not None:
for i in range(p.n):
if not p.l:
traverse(p.child_ptr[i])
print(p.d[i], end=" ")
if not p.l:
traverse(p.child_ptr[p.n])
#sort the tree
def sort(p, n):
for i in range(n):
for j in range(i, n+1):
if p[i] > p[j]:
p[i], p[j] = p[j], p[i]
def split_child(x, i):
np3 = init()
#create new node
np3.l = True
if i == -1:
mid = x.d[2]
#find mid
x.d[2] = 0
x.n -= 1
np1 = init()
np1.l = False
x.l = True
for j in range(3, 6):
np3.d[j-3] = x.d[j]
np3.child_ptr[j-3] = x.child_ptr[j]
np3.n += 1
x.d[j] = 0
x.n -= 1
for j in range(6):
x.child_ptr[j] = None
np1.d[0] = mid
np1.child_ptr[np1.n] = x
np1.child_ptr[np1.n + 1] = np3
np1.n += 1
return np1
else:
y = x.child_ptr[i]
mid = y.d[2]
y.d[2] = 0
y.n -= 1
for j in range(3, 6):
np3.d[j-3] = y.d[j]
np3.n += 1
y.d[j] = 0
y.n -= 1
x.child_ptr[i + 1] = y
x.child_ptr[i + 1] = np3
return mid
def insert(a):
global r, x
if r is None:
r = init()
x = r
else:
if x.l and x.n == 6:
t = split_child(x, -1)
x = r
for i in range(x.n):
if a > x.d[i] and a < x.d[i + 1]:
i += 1
break
elif a < x.d[0]:
break
else:
continue
x = x.child_ptr[i]
else:
while not x.l:
for i in range(x.n):
if a > x.d[i] and a < x.d[i + 1]:
i += 1
break
elif a < x.d[0]:
break
else:
continue
if x.child_ptr[i].n == 6:
t = split_child(x, i)
x.d[x.n] = t
x.n += 1
continue
else:
x = x.child_ptr[i]
x.d[x.n] = a
sort(x.d, x.n)
x.n += 1
if __name__ == '__main__':
r = None
x = None
insert(10)
insert(20)
insert(30)
insert(40)
insert(50)
print("B tree:")
traverse(r)
Output
B tree: 10 20 30 40 50
B+ Trees
The B+ trees are extensions of B trees designed to make the insertion, deletion and searching operations more efficient.
The properties of B+ trees are similar to the properties of B trees, except that the B trees can store keys and records in all internal nodes and leaf nodes while B+ trees store records in leaf nodes and keys in internal nodes. One profound property of the B+ tree is that all the leaf nodes are connected to each other in a single linked list format and a data pointer is available to point to the data present in disk file. This helps fetch the records in equal numbers of disk access.
Since the size of main memory is limited, B+ trees act as the data storage for the records that couldnt be stored in the main memory. For this, the internal nodes are stored in the main memory and the leaf nodes are stored in the secondary memory storage.
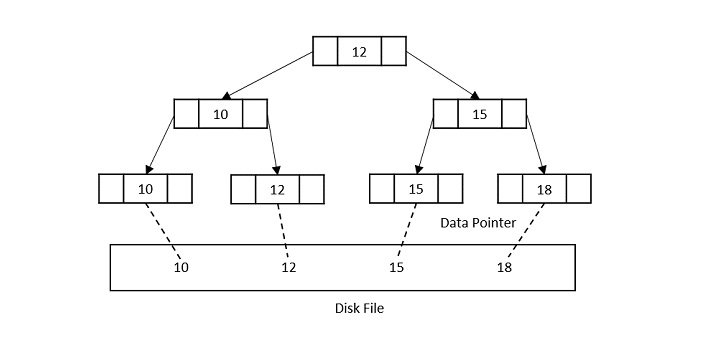
Properties of B+ trees
Every node in a B+ Tree, except root, will hold a maximum of m children and (m-1) keys, and a minimum of $\mathrm{\left \lceil \frac{m}{2}\right \rceil}$ children and $\mathrm{\left \lceil \frac{m-1}{2}\right \rceil}$ keys, since the order of the tree is m.
The root node must have no less than two children and at least one search key.
All the paths in a B tree must end at the same level, i.e. the leaf nodes must be at the same level.
A B+ tree always maintains sorted data.
Basic Operations of B+ Trees
The operations supported in B+ trees are Insertion, deletion and searching with the time complexity of O(log n) for every operation.
They are almost similar to the B tree operations as the base idea to store data in both data structures is same. However, the difference occurs as the data is stored only in the leaf nodes of a B+ trees, unlike B trees.
Insertion
The insertion to a B+ tree starts at a leaf node.
Step 1 − Calculate the maximum and minimum number of keys to be added onto the B+ tree node.

Step 2 − Insert the elements one by one accordingly into a leaf node until it exceeds the maximum key number.
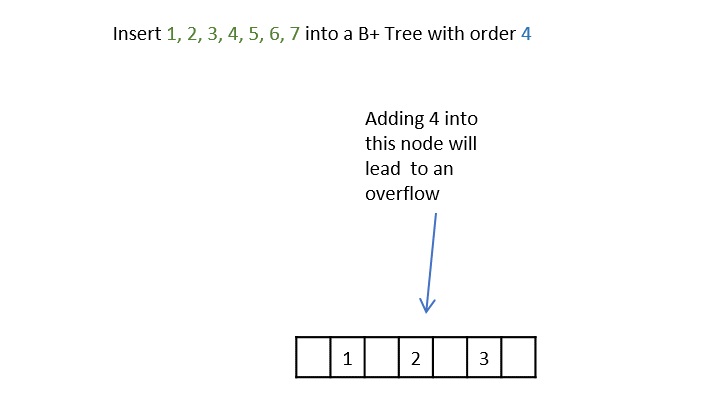
Step 3 − The node is split into half where the left child consists of minimum number of keys and the remaining keys are stored in the right child.
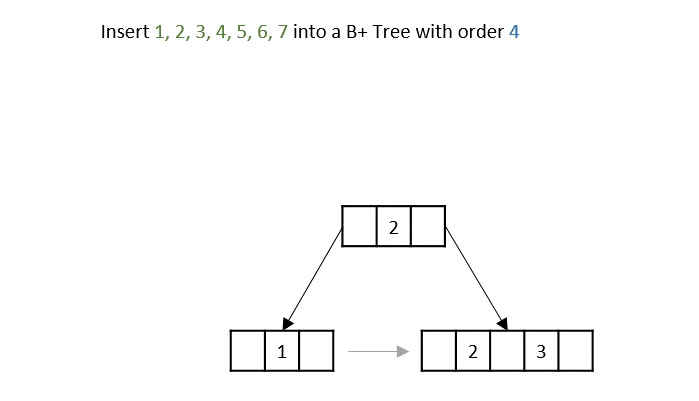
Step 4 − But if the internal node also exceeds the maximum key property, the node is split in half where the left child consists of the minimum keys and remaining keys are stored in the right child. However, the smallest number in the right child is made the parent.
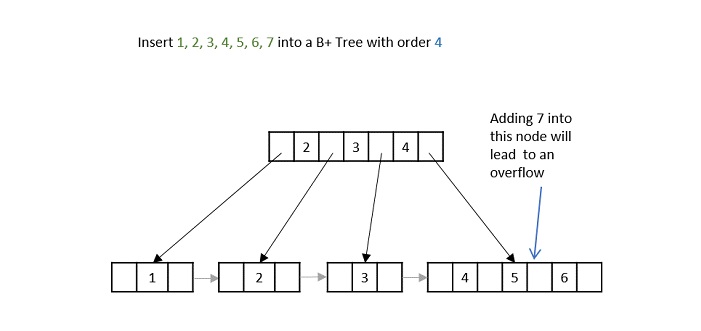
Step 5 − If both the leaf node and internal node have the maximum keys, both of them are split in the similar manner and the smallest key in the right child is added to the parent node.
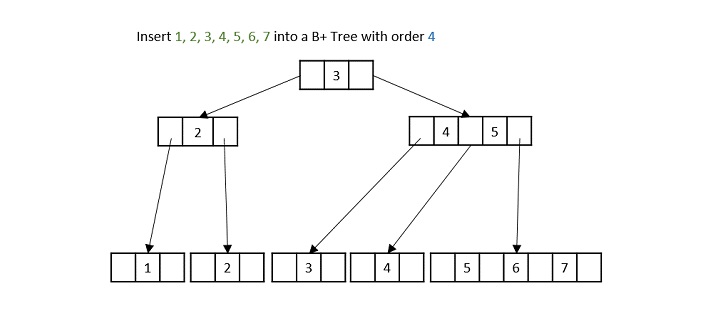
Deletion
The deletion operation in a B+ tree, we need to consider the redundancy in the data structure.
Case 1 − If the key is present in a leaf node which has more than minimal number of keys, without its copy present in the internal nodes, simple delete it.
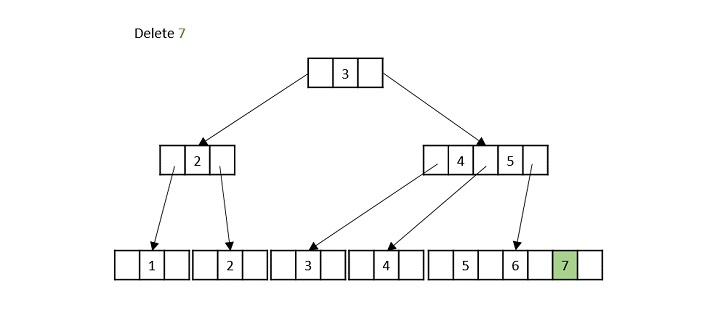
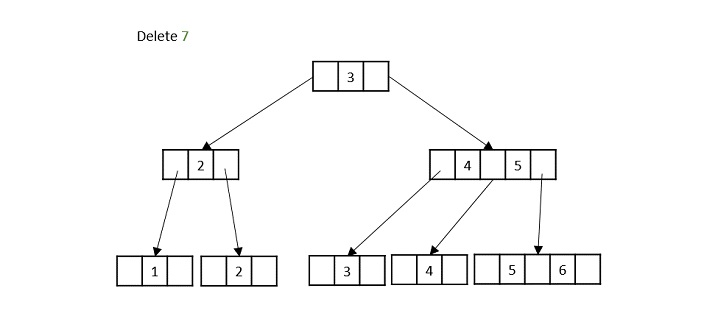
Case 2 − If the key is present in a leaf node with exactly minimal number of keys and a copy of it is not present in the internal nodes, borrow a key from its sibling node and delete the desired key.
Case 3 − If the key present in the leaf node has its copy in the internal nodes, there are multiple scenarios possible −
More than minimal keys present in both leaf node and internal node: simply delete the key and add the inorder successor to the internal node only.
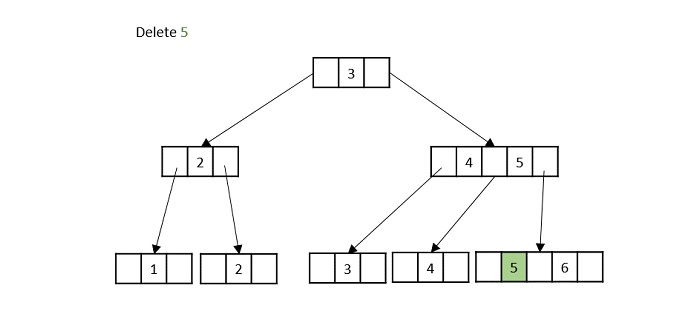
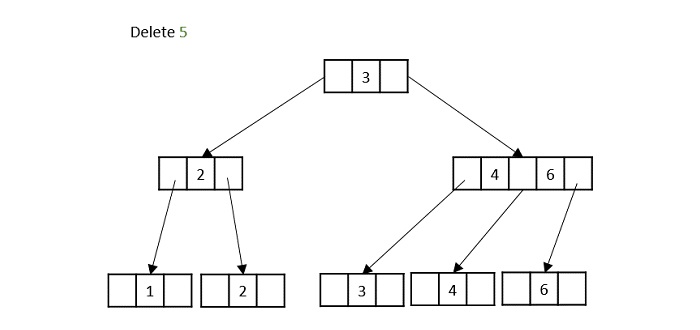
Exact minimum number of keys present in the leaf node: delete the node and borrow a node from its immediate sibling and replace its value in internal node as well.
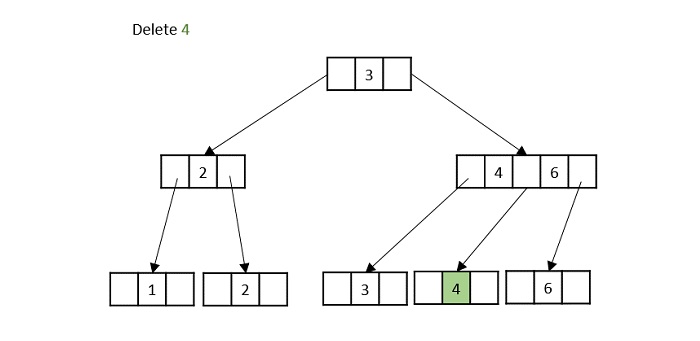
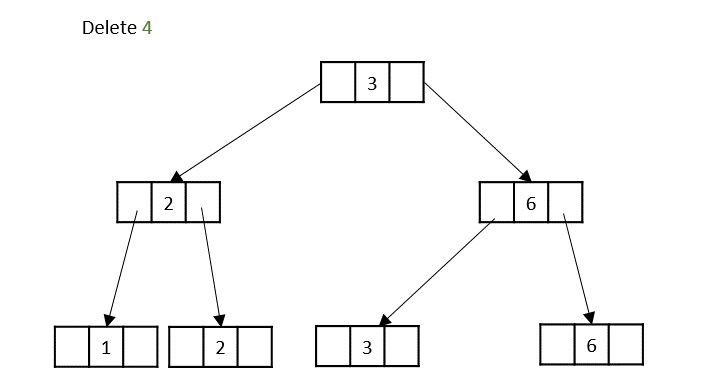
If the copy of the leaf node to be delete is in its grandparent, delete the node and remove the empty space. The grandparent is filled with the inorder successor of the deleted node.
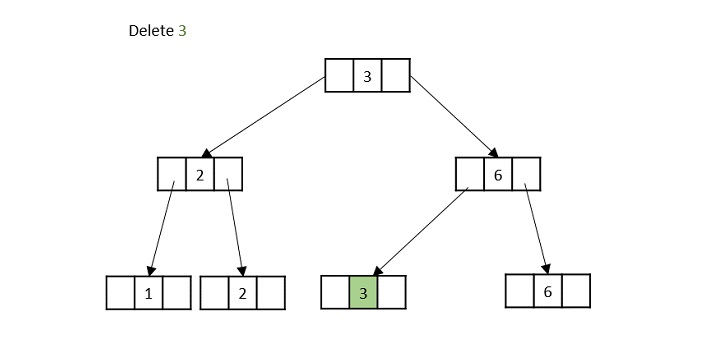
Case 4 − If the key to be deleted is in a node violating the minimum keys property, both its parent and sibling have minimum number of keys, delete the key and merge its sibling with its parent.
Example
// C program for Bplus tree
#include <stdio.h>
#include <stdlib.h>
struct BplusTree {
int *d;
struct BplusTree **child_ptr;
int l;
int n;
};
struct BplusTree *r = NULL, *np = NULL, *x = NULL;
struct BplusTree* init() {
//to create nodes
int i;
np = (struct BplusTree*)malloc(sizeof(struct BplusTree));
np->d = (int*)malloc(6 * sizeof(int)); // order 6
np->child_ptr = (struct BplusTree**)malloc(7 * sizeof(struct BplusTree*));
np->l = 1;
np->n = 0;
for (i = 0; i < 7; i++) {
np->child_ptr[i] = NULL;
}
return np;
}
void traverse(struct BplusTree *p) {
//traverse tree
printf("\n");
int i;
for (i = 0; i < p->n; i++) {
if (p->l == 0) {
traverse(p->child_ptr[i]);
}
printf(" %d", p->d[i]);
}
if (p->l == 0) {
traverse(p->child_ptr[i]);
}
printf("\n");
}
void sort(int *p, int n) {
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] > p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
int split_child(struct BplusTree *x, int i) {
int j, mid;
struct BplusTree *np1, *np3, *y;
np3 = init();
np3->l = 1;
if (i == -1) {
mid = x->d[2];
x->d[2] = 0;
x->n--;
np1 = init();
np1->l = 0;
x->l = 1;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = x->d[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->d[j] = 0;
x->n--;
}
for (j = 0; j < 6; j++) {
x->child_ptr[j] = NULL;
}
np1->d[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
r = np1;
} else {
y = x->child_ptr[i];
mid = y->d[2];
y->d[2] = 0;
y->n--;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = y->d[j];
np3->n++;
y->d[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insert(int a) {
int i, t;
x = r;
if (x == NULL) {
r = init();
x = r;
} else {
if (x->l == 1 && x->n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < x->n; i++) {
if (a > x->d[i] && a < x->d[i + 1]) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
x = x->child_ptr[i];
} else {
while (x->l == 0) {
for (i = 0; i < x->n; i++) {
if (a > x->d[i] && a < x->d[i + 1]) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
if (x->child_ptr[i]->n == 6) {
t = split_child(x, i);
x->d[x->n] = t;
x->n++;
continue;
} else {
x = x->child_ptr[i];
}
}
}
}
x->d[x->n] = a;
sort(x->d, x->n);
x->n++;
}
int main() {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
printf("B+ tree:\n");
traverse(r);
return 0;
}
Output
B+ tree: 10 20 30 40 50
#include<iostream>
using namespace std;
struct BplusTree {
int *d;
BplusTree **child_ptr;
bool l;
int n;
}
*r = NULL, *np = NULL, *x = NULL;
BplusTree* init() { //to create nodes
int i;
np = new BplusTree;
np->d = new int[6];//order 6
np->child_ptr = new BplusTree *[7];
np->l = true;
np->n = 0;
for (i = 0; i < 7; i++) {
np->child_ptr[i] = NULL;
}
return np;
}
void traverse(BplusTree *p) { //traverse tree
cout<<endl;
int i;
for (i = 0; i < p->n; i++) {
if (p->l == false) {
traverse(p->child_ptr[i]);
}
cout << " " << p->d[i];
}
if (p->l == false) {
traverse(p->child_ptr[i]);
}
cout<<endl;
}
void sort(int *p, int n) { //sort the tree
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] >p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
int split_child(BplusTree *x, int i) {
int j, mid;
BplusTree *np1, *np3, *y;
np3 = init();
np3->l = true;
if (i == -1) {
mid = x->d[2];
x->d[2] = 0;
x->n--;
np1 = init();
np1->l = false;
x->l = true;
for (j = 3; j < 6; j++) {
np3->d[j - 3] = x->d[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->d[j] = 0;
x->n--;
}
for (j = 0; j < 6; j++) {
x->child_ptr[j] = NULL;
}
np1->d[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
r = np1;
} else {
y = x->child_ptr[i];
mid = y->d[2];
y->d[2] = 0;
y->n--;
for (j = 3; j <6 ; j++) {
np3->d[j - 3] = y->d[j];
np3->n++;
y->d[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insert(int a) {
int i, t;
x = r;
if (x == NULL) {
r = init();
x = r;
} else {
if (x->l== true && x->n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < (x->n); i++) {
if ((a >x->d[i]) && (a < x->d[i + 1])) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
x = x->child_ptr[i];
} else {
while (x->l == false) {
for (i = 0; i < (x->n); i++) {
if ((a >x->d[i]) && (a < x->d[i + 1])) {
i++;
break;
} else if (a < x->d[0]) {
break;
} else {
continue;
}
}
if ((x->child_ptr[i])->n == 6) {
t = split_child(x, i);
x->d[x->n] = t;
x->n++;
continue;
} else {
x = x->child_ptr[i];
}
}
}
}
x->d[x->n] = a;
sort(x->d, x->n);
x->n++;
}
int main() {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
cout<<"B+ tree:\n";
traverse(r);
}
Output
B+ tree: 10 20 30 40 50
//Java program for Bplus code
import java.util.*;
class BplusTree {
int[] d;
BplusTree[] child_ptr;
boolean l;
int n;
}
public class Main {
static BplusTree r = null, np = null, x = null;
static BplusTree init() { // to create nodes
int i;
np = new BplusTree();
np.d = new int[6]; // order 6
np.child_ptr = new BplusTree[7];
np.l = true;
np.n = 0;
for (i = 0; i < 7; i++) {
np.child_ptr[i] = null;
}
return np;
}
static void traverse(BplusTree p) { // traverse tree
System.out.println();
int i;
for (i = 0; i < p.n; i++) {
if (p.l == false) {
traverse(p.child_ptr[i]);
}
System.out.print(" " + p.d[i]);
}
if (p.l == false) {
traverse(p.child_ptr[i]);
}
System.out.println();
}
static void sort(int[] p, int n) { // sort the tree
int i, j, t;
for (i = 0; i < n; i++) {
for (j = i; j <= n; j++) {
if (p[i] > p[j]) {
t = p[i];
p[i] = p[j];
p[j] = t;
}
}
}
}
static int split_child(BplusTree x, int i) {
int j, mid;
BplusTree np1, np3, y;
np3 = init();
np3.l = true;
if (i == -1) {
mid = x.d[2];
x.d[2] = 0;
x.n--;
np1 = init();
np1.l = false;
x.l = true;
for (j = 3; j < 6; j++) {
np3.d[j - 3] = x.d[j];
np3.child_ptr[j - 3] = x.child_ptr[j];
np3.n++;
x.d[j] = 0;
x.n--;
}
for (j = 0; j < 6; j++) {
x.child_ptr[j] = null;
}
np1.d[0] = mid;
np1.child_ptr[np1.n] = x;
np1.child_ptr[np1.n + 1] = np3;
np1.n++;
r = np1;
} else {
y = x.child_ptr[i];
mid = y.d[2];
y.d[2] = 0;
y.n--;
for (j = 3; j < 6; j++) {
np3.d[j - 3] = y.d[j];
np3.n++;
y.d[j] = 0;
y.n--;
}
x.child_ptr[i + 1] = y;
x.child_ptr[i + 1] = np3;
}
return mid;
}
static void insert(int a) {
int i, t;
x = r;
if (x == null) {
r = init();
x = r;
} else {
if (x.l == true && x.n == 6) {
t = split_child(x, -1);
x = r;
for (i = 0; i < x.n; i++) {
if (a > x.d[i] && a < x.d[i + 1]) {
i++;
break;
} else if (a < x.d[0]) {
break;
} else {
continue;
}
}
x = x.child_ptr[i];
} else {
while (x.l == false) {
for (i = 0; i < x.n; i++) {
if (a > x.d[i] && a < x.d[i + 1]) {
i++;
break;
} else if (a < x.d[0]) {
break;
} else {
continue;
}
}
if (x.child_ptr[i].n == 6) {
t = split_child(x, i);
x.d[x.n] = t;
x.n++;
continue;
} else {
x = x.child_ptr[i];
}
}
}
}
x.d[x.n] = a;
sort(x.d, x.n);
x.n++;
}
public static void main(String[] args) {
int i, n, t;
insert(10);
insert(20);
insert(30);
insert(40);
insert(50);
System.out.println("B+ tree:");
traverse(r);
}
}
Output
B+ tree: 10 20 30 40 50
#Python Program for Bplus tree
#to create nodes
class BplusTree:
def __init__(self):
self.d = [0] * 6 # order 6
self.child_ptr = [None] * 7
self.l = True
self.n = 0
def init():
np = BplusTree()
np.l = True
np.n = 0
return np
#traverse tree
def traverse(p):
print()
for i in range(p.n):
if not p.l:
traverse(p.child_ptr[i])
print(" ", p.d[i], end="")
if not p.l:
traverse(p.child_ptr[p.n])
print()
#sort the tree
def sort(p, n):
for i in range(n):
for j in range(i, n + 1):
if p[i] > p[j]:
p[i], p[j] = p[j], p[i]
def split_child(x, i):
np3 = init()
np3.l = True
if i == -1:
mid = x.d[2]
x.d[2] = 0
x.n -= 1
np1 = init()
np1.l = False
x.l = True
for j in range(3, 6):
np3.d[j - 3] = x.d[j]
np3.child_ptr[j - 3] = x.child_ptr[j]
np3.n += 1
x.d[j] = 0
x.n -= 1
for j in range(6):
x.child_ptr[j] = None
np1.d[0] = mid
np1.child_ptr[np1.n] = x
np1.child_ptr[np1.n + 1] = np3
np1.n += 1
r = np1
else:
y = x.child_ptr[i]
mid = y.d[2]
y.d[2] = 0
y.n -= 1
for j in range(3, 6):
np3.d[j - 3] = y.d[j]
np3.n += 1
y.d[j] = 0
y.n -= 1
x.child_ptr[i + 1] = y
x.child_ptr[i + 1] = np3
return mid
def insert(a):
global r, x
x = r
if x is None:
r = init()
x = r
else:
if x.l and x.n == 6:
t = split_child(x, -1)
x = r
for i in range(x.n):
if a > x.d[i] and a < x.d[i + 1]:
i += 1
break
elif a < x.d[0]:
break
else:
continue
x = x.child_ptr[i]
else:
while not x.l:
for i in range(x.n):
if a > x.d[i] and a < x.d[i + 1]:
i += 1
break
elif a < x.d[0]:
break
else:
continue
if x.child_ptr[i].n == 6:
t = split_child(x, i)
x.d[x.n] = t
x.n += 1
continue
else:
x = x.child_ptr[i]
x.d[x.n] = a
sort(x.d, x.n)
x.n += 1
r = None
x = None
insert(10)
insert(20)
insert(30)
insert(40)
insert(50)
print("B+ tree:")
traverse(r)
Output
B+ tree: 10 20 30 40 50
Splay Trees
Splay trees are the altered versions of the Binary Search Trees, since it contains all the operations of BSTs, like insertion, deletion and searching, followed by another extended operation called splaying.
For instance, a value A is supposed to be inserted into the tree. If the tree is empty, add A to the root of the tree and exit; but if the tree is not empty, use binary search insertion operation to insert the element and then perform splaying on the new node.
Similarly, after searching an element in the splay tree, the node consisting of the element must be splayed as well.
But how do we perform splaying? Splaying, in simpler terms, is just a process to bring an operational node to the root. There are six types of rotations for it.
Zig rotation
Zag rotation
Zig-Zig rotation
Zag-Zag rotation
Zig-Zag rotation
Zag-Zig rotation
Zig rotation
The zig rotations are performed when the operational node is either the root node or the left child node of the root node. The node is rotated towards its right.
After the shift, the tree will look like −
Zag rotation
The zag rotations are also performed when the operational node is either the root node or the right child nod of the root node. The node is rotated towards its left.
The operational node becomes the root node after the shift −
Zig-Zig rotation
The zig-zig rotations are performed when the operational node has both parent and a grandparent. The node is rotated two places towards its right.
The first rotation will shift the tree to one position right −
The second right rotation will once again shift the node for one position. The final tree after the shift will look like this −
Zag-Zag rotation
The zag-zag rotations are also performed when the operational node has both parent and a grandparent. The node is rotated two places towards its left.
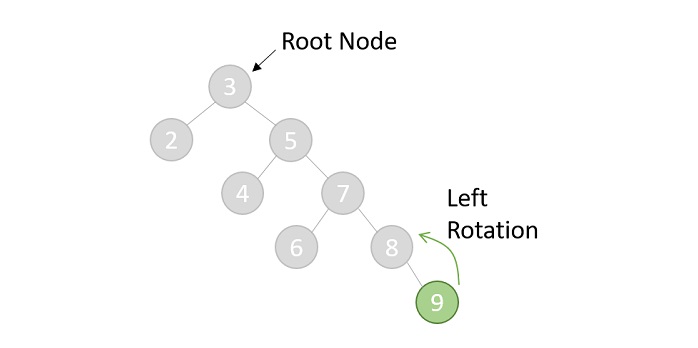
After the first rotation, the tree will look like −
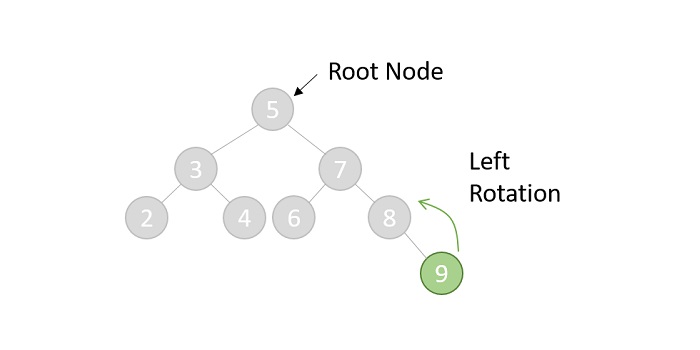
Then the final tree after the second rotation is given as follows. However, the operational node is still not the root so the splaying is considered incomplete. Hence, other suitable rotations are again applied in this case until the node becomes the root.
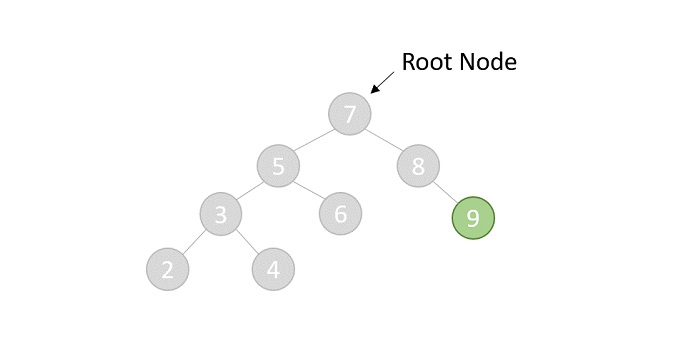
Zig-Zag rotation
The zig-zag rotations are performed when the operational node has both a parent and a grandparent. But the difference is the grandparent, parent and child are in LRL format. The node is rotated first towards its right followed by left.
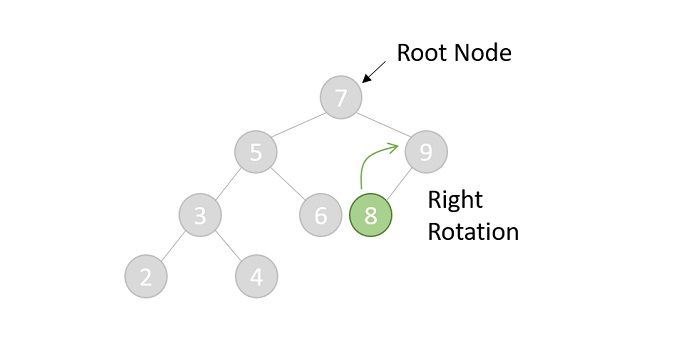
After the first rotation, the tree is −
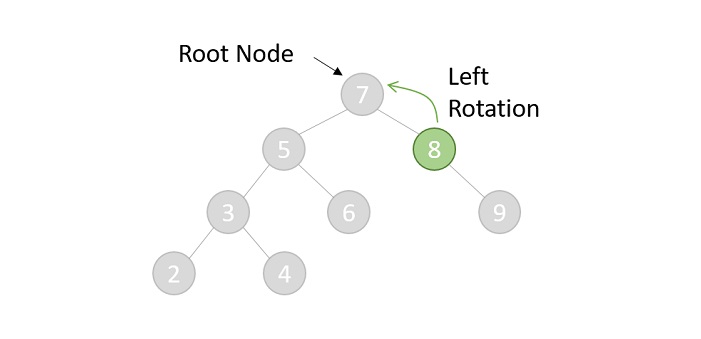
The final tree after the second rotation −
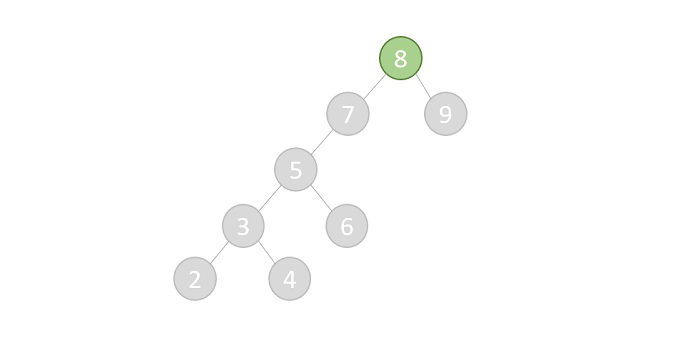
Zag-Zig rotation
The zag-zig rotations are also performed when the operational node has both parent and grandparent. But the difference is the grandparent, parent and child are in RLR format. The node is rotated first towards its left followed by right.
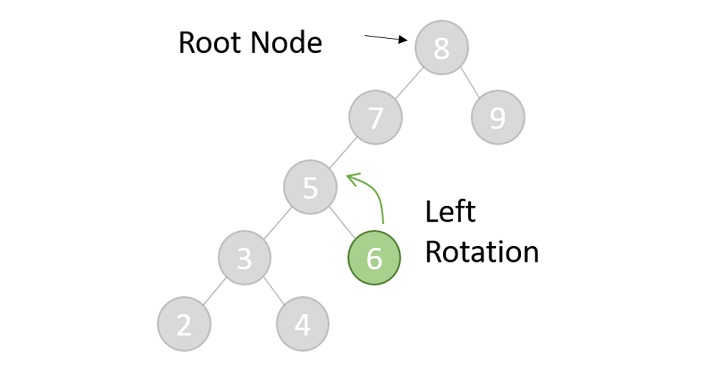
First rotation is performed, the tree is obtained as −
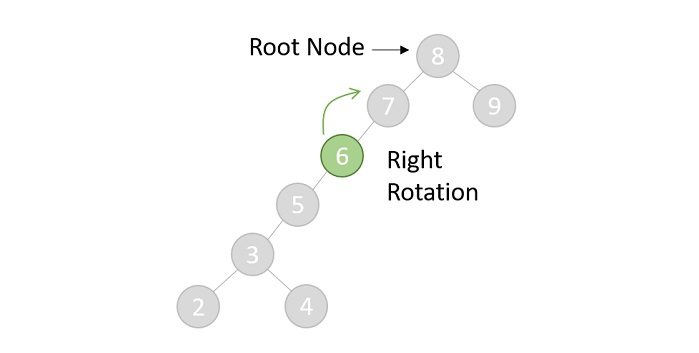
After second rotation, the final tree is given as below. However, the operational node is not the root node yet so one more rotation needs to be performed to make the said node as the root.
Basic Operations of Splay Trees
A splay contains the same basic operations that a Binary Search Tree provides with: Insertion, Deletion, and Search. However, after every operation there is an additional operation that differs them from Binary Search tree operations: Splaying. We have learned about Splaying already so let us understand the procedures of the other operations.
Insertion
The insertion operation in a Splay tree is performed in the exact same way insertion in a binary search tree is performed. The procedure to perform the insertion in a splay tree is given as follows −
Check whether the tree is empty; if yes, add the new node and exit

If the tree is not empty, add the new node to the existing tree using the binary search insertion.
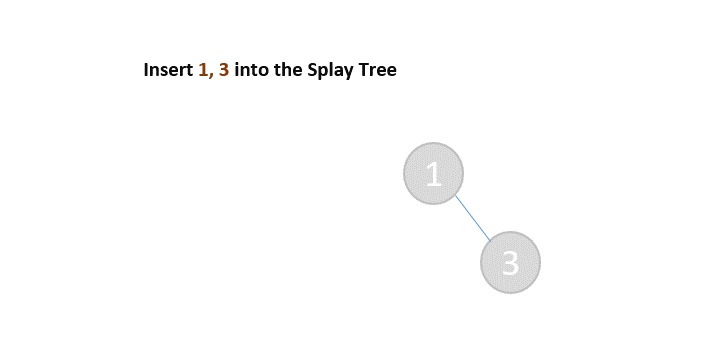
Then, suitable splaying is chosen and applied on the newly added node.
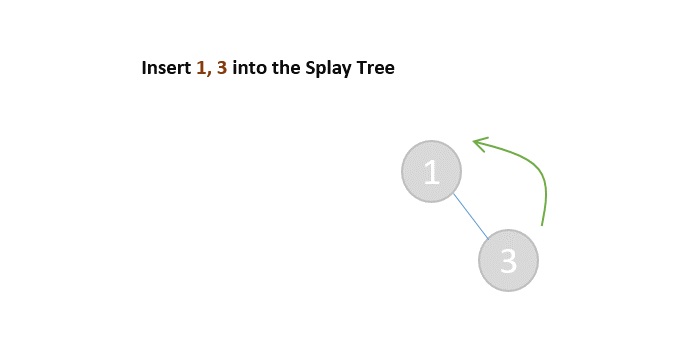
Zag (Left) Rotation is applied on the new node
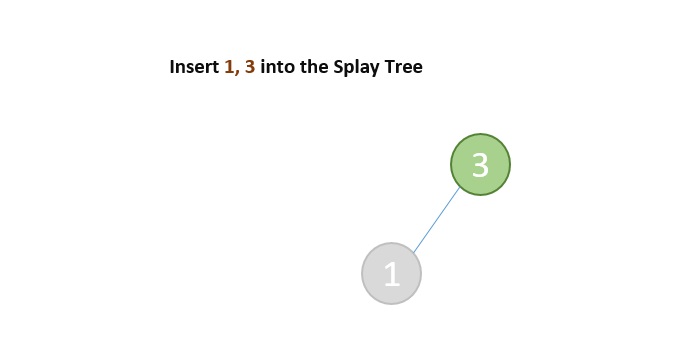
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
struct node* Node = (struct node*)malloc(sizeof(struct node));
Node->data = data;
Node->leftChild = Node->rightChild = NULL;
return (Node);
}
struct node* rightRotate(struct node *x){
struct node *y = x->leftChild;
x->leftChild = y->rightChild;
y->rightChild = x;
return y;
}
struct node* leftRotate(struct node *x){
struct node *y = x->rightChild;
x->rightChild = y->leftChild;
y->leftChild = x;
return y;
}
struct node* splay(struct node *root, int data){
if (root == NULL || root->data == data)
return root;
if (root->data > data) {
if (root->leftChild == NULL) return root;
if (root->leftChild->data > data) {
root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
root = rightRotate(root);
} else if (root->leftChild->data < data) {
root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
if (root->leftChild->rightChild != NULL)
root->leftChild = leftRotate(root->leftChild);
}
return (root->leftChild == NULL)? root: rightRotate(root);
} else {
if (root->rightChild == NULL) return root;
if (root->rightChild->data > data) {
root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
if (root->rightChild->leftChild != NULL)
root->rightChild = rightRotate(root->rightChild);
} else if (root->rightChild->data < data) {
root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
root = leftRotate(root);
}
return (root->rightChild == NULL)? root: leftRotate(root);
}
}
struct node* insert(struct node *root, int k){
if (root == NULL) return newNode(k);
root = splay(root, k);
if (root->data == k) return root;
struct node *newnode = newNode(k);
if (root->data > k) {
newnode->rightChild = root;
newnode->leftChild = root->leftChild;
root->leftChild = NULL;
} else {
newnode->leftChild = root;
newnode->rightChild = root->rightChild;
root->rightChild = NULL;
}
return newnode;
}
void printTree(struct node *root){
if (root == NULL)
return;
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct node* root = newNode(34);
root->leftChild = newNode(15);
root->rightChild = newNode(40);
root->leftChild->leftChild = newNode(12);
root->leftChild->leftChild->rightChild = newNode(14);
root->rightChild->rightChild = newNode(59);
printf("The Splay tree is: \n");
printTree(root);
return 0;
}
Output
The Splay tree is: 12 14 15 34 40 59
#include <iostream>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
struct node* Node = (struct node*)malloc(sizeof(struct node));
Node->data = data;
Node->leftChild = Node->rightChild = NULL;
return (Node);
}
struct node* rightRotate(struct node *x){
struct node *y = x->leftChild;
x->leftChild = y->rightChild;
y->rightChild = x;
return y;
}
struct node* leftRotate(struct node *x){
struct node *y = x->rightChild;
x->rightChild = y->leftChild;
y->leftChild = x;
return y;
}
struct node* splay(struct node *root, int data){
if (root == NULL || root->data == data)
return root;
if (root->data > data) {
if (root->leftChild == NULL) return root;
if (root->leftChild->data > data) {
root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
root = rightRotate(root);
} else if (root->leftChild->data < data) {
root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
if (root->leftChild->rightChild != NULL)
root->leftChild = leftRotate(root->leftChild);
}
return (root->leftChild == NULL)? root: rightRotate(root);
} else {
if (root->rightChild == NULL) return root;
if (root->rightChild->data > data) {
root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
if (root->rightChild->leftChild != NULL)
root->rightChild = rightRotate(root->rightChild);
} else if (root->rightChild->data < data) {
root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
root = leftRotate(root);
}
return (root->rightChild == NULL)? root: leftRotate(root);
}
}
struct node* insert(struct node *root, int k){
if (root == NULL) return newNode(k);
root = splay(root, k);
if (root->data == k) return root;
struct node *newnode = newNode(k);
if (root->data > k) {
newnode->rightChild = root;
newnode->leftChild = root->leftChild;
root->leftChild = NULL;
} else {
newnode->leftChild = root;
newnode->rightChild = root->rightChild;
root->rightChild = NULL;
}
return newnode;
}
void printTree(struct node *root){
if (root == NULL)
return;
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct node* root = newNode(34);
root->leftChild = newNode(15);
root->rightChild = newNode(40);
root->leftChild->leftChild = newNode(12);
root->leftChild->leftChild->rightChild = newNode(14);
root->rightChild->rightChild = newNode(59);
printf("The Splay tree is: \n");
printTree(root);
return 0;
}
Output
The Splay tree is: 12 14 15 34 40 59
import java.io.*;
public class SplayTree {
static class node {
int data;
node leftChild, rightChild;
};
static node newNode(int data) {
node Node = new node();
Node.data = data;
Node.leftChild = Node.rightChild = null;
return (Node);
}
static node rightRotate(node x) {
node y = x.leftChild;
x.leftChild = y.rightChild;
y.rightChild = x;
return y;
}
static node leftRotate(node x) {
node y = x.rightChild;
x.rightChild = y.leftChild;
y.leftChild = x;
return y;
}
static node splay(node root, int data) {
if (root == null || root.data == data)
return root;
if (root.data > data) {
if (root.leftChild == null) return root;
if (root.leftChild.data > data) {
root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
root = rightRotate(root);
} else if (root.leftChild.data < data) {
root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
if (root.leftChild.rightChild != null)
root.leftChild = leftRotate(root.leftChild);
}
return (root.leftChild == null)? root: rightRotate(root);
} else {
if (root.rightChild == null) return root;
if (root.rightChild.data > data) {
root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
if (root.rightChild.leftChild != null)
root.rightChild = rightRotate(root.rightChild);
} else if (root.rightChild.data < data) {
root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
root = leftRotate(root);
}
return (root.rightChild == null)? root: leftRotate(root);
}
}
static node insert(node root, int k) {
if (root == null) return newNode(k);
root = splay(root, k);
if (root.data == k) return root;
node newnode = newNode(k);
if (root.data > k) {
newnode.rightChild = root;
newnode.leftChild = root.leftChild;
root.leftChild = null;
} else {
newnode.leftChild = root;
newnode.rightChild = root.rightChild;
root.rightChild = null;
}
return newnode;
}
static void printTree(node root) {
if (root == null)
return;
if (root != null) {
printTree(root.leftChild);
System.out.print(root.data + " ");
printTree(root.rightChild);
}
}
public static void main(String args[]) {
node root = newNode(34);
root.leftChild = newNode(15);
root.rightChild = newNode(40);
root.leftChild.leftChild = newNode(12);
root.leftChild.leftChild.rightChild = newNode(14);
root.rightChild.rightChild = newNode(59);
System.out.println("The Splay tree is: ");
printTree(root);
}
}
Output
The Splay tree is: 12 14 15 34 40 59
#Python Code for Insertion Operation of Splay Trees
class Node:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild = None
def newNode(data):
return Node(data)
def rightRotate(x):
y = x.leftChild
x.leftChild = y.rightChild
y.rightChild = x
return y
def leftRotate(x):
y = x.rightChild
x.rightChild = y.leftChild
y.leftChild = x
return y
def splay(root, data):
if root is None or root.data == data:
return root
if root.data > data:
if root.leftChild is None:
return root
if root.leftChild.data > data:
root.leftChild.leftChild = splay(root.leftChild.leftChild, data)
root = rightRotate(root)
elif root.leftChild.data < data:
root.leftChild.rightChild = splay(root.leftChild.rightChild, data)
if root.leftChild.rightChild is not None:
root.leftChild = leftRotate(root.leftChild)
return root if root.leftChild is None else rightRotate(root)
else:
if root.rightChild is None:
return root
if root.rightChild.data > data:
root.rightChild.leftChild = splay(root.rightChild.leftChild, data)
if root.rightChild.leftChild is not None:
root.rightChild = rightRotate(root.rightChild)
elif root.rightChild.data < data:
root.rightChild.rightChild = splay(root.rightChild.rightChild, data)
root = leftRotate(root)
return root if root.rightChild is None else leftRotate(root)
def insert(root, k):
if root is None:
return newNode(k)
root = splay(root, k)
if root.data == k:
return root
newnode = newNode(k)
if root.data > k:
newnode.rightChild = root
newnode.leftChild = root.leftChild
root.leftChild = None
else:
newnode.leftChild = root
newnode.rightChild = root.rightChild
root.rightChild = None
return newnode
def printTree(root):
if root is None:
return
if root is not None:
printTree(root.leftChild)
print(root.data, end=" ")
printTree(root.rightChild)
if __name__ == "__main__":
root = newNode(34)
root.leftChild = newNode(15)
root.rightChild = newNode(40)
root.leftChild.leftChild = newNode(12)
root.leftChild.leftChild.rightChild = newNode(14)
root.rightChild.rightChild = newNode(59)
print("The Splay tree is: ")
printTree(root)
Output
The Splay tree is: 12 14 15 34 40 59
Deletion
The deletion operation in a splay tree is performed as following −
Apply splaying operation on the node to be deleted.
Once, the node is made the root, delete the node.
Now, the tree is split into two trees, the left subtree and the right subtree; with their respective first nodes as the root nodes: say root_left and root_right.
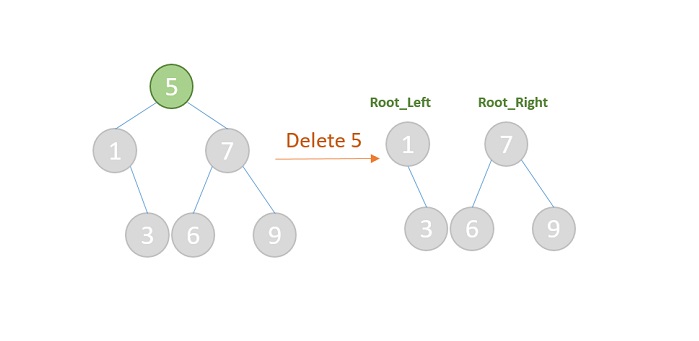
If root_left is a NULL value, then the root_right will become the root of the tree. And vice versa.
But if both root_left and root_right are not NULL values, then select the maximum value from the left subtree and make it the new root by connecting the subtrees.
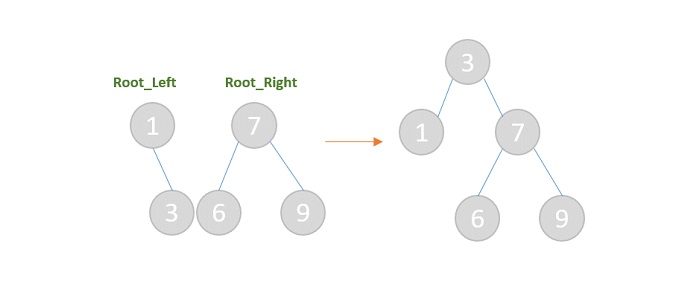
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
struct node* Node = (struct node*)malloc(sizeof(struct node));
Node->data = data;
Node->leftChild = Node->rightChild = NULL;
return (Node);
}
struct node* rightRotate(struct node *x){
struct node *y = x->leftChild;
x->leftChild = y->rightChild;
y->rightChild = x;
return y;
}
struct node* leftRotate(struct node *x){
struct node *y = x->rightChild;
x->rightChild = y->leftChild;
y->leftChild = x;
return y;
}
struct node* splay(struct node *root, int data){
if (root == NULL || root->data == data)
return root;
if (root->data > data) {
if (root->leftChild == NULL) return root;
if (root->leftChild->data > data) {
root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
root = rightRotate(root);
} else if (root->leftChild->data < data) {
root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
if (root->leftChild->rightChild != NULL)
root->leftChild = leftRotate(root->leftChild);
}
return (root->leftChild == NULL)? root: rightRotate(root);
} else {
if (root->rightChild == NULL) return root;
if (root->rightChild->data > data) {
root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
if (root->rightChild->leftChild != NULL)
root->rightChild = rightRotate(root->rightChild);
} else if (root->rightChild->data < data) {
root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
root = leftRotate(root);
}
return (root->rightChild == NULL)? root: leftRotate(root);
}
}
struct node* insert(struct node *root, int k){
if (root == NULL) return newNode(k);
root = splay(root, k);
if (root->data == k) return root;
struct node *newnode = newNode(k);
if (root->data > k) {
newnode->rightChild = root;
newnode->leftChild = root->leftChild;
root->leftChild = NULL;
} else {
newnode->leftChild = root;
newnode->rightChild = root->rightChild;
root->rightChild = NULL;
}
return newnode;
}
struct node* deletenode(struct node* root, int data){
struct node* temp;
if (root == NULL)
return NULL;
root = splay(root, data);
if (data != root->data)
return root;
if (!root->leftChild) {
temp = root;
root = root->rightChild;
} else {
temp = root;
root = splay(root->leftChild, data);
root->rightChild = temp->rightChild;
}
free(temp);
return root;
}
void printTree(struct node *root){
if (root == NULL)
return;
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct node* root = newNode(34);
root->leftChild = newNode(15);
root->rightChild = newNode(40);
printf("The Splay tree is \n");
printTree(root);
root = deletenode(root, 40);
printf("\nThe Splay tree after deletion is \n");
printTree(root);
return 0;
}
Output
The Splay tree is 15 34 40 The Splay tree after deletion is 15 34
#include <iostream>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
struct node* Node = (struct node*)malloc(sizeof(struct node));
Node->data = data;
Node->leftChild = Node->rightChild = NULL;
return (Node);
}
struct node* rightRotate(struct node *x){
struct node *y = x->leftChild;
x->leftChild = y->rightChild;
y->rightChild = x;
return y;
}
struct node* leftRotate(struct node *x){
struct node *y = x->rightChild;
x->rightChild = y->leftChild;
y->leftChild = x;
return y;
}
struct node* splay(struct node *root, int data){
if (root == NULL || root->data == data)
return root;
if (root->data > data) {
if (root->leftChild == NULL) return root;
if (root->leftChild->data > data) {
root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
root = rightRotate(root);
} else if (root->leftChild->data < data) {
root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
if (root->leftChild->rightChild != NULL)
root->leftChild = leftRotate(root->leftChild);
}
return (root->leftChild == NULL)? root: rightRotate(root);
} else {
if (root->rightChild == NULL) return root;
if (root->rightChild->data > data) {
root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
if (root->rightChild->leftChild != NULL)
root->rightChild = rightRotate(root->rightChild);
} else if (root->rightChild->data < data) {
root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
root = leftRotate(root);
}
return (root->rightChild == NULL)? root: leftRotate(root);
}
}
struct node* insert(struct node *root, int k){
if (root == NULL) return newNode(k);
root = splay(root, k);
if (root->data == k) return root;
struct node *newnode = newNode(k);
if (root->data > k) {
newnode->rightChild = root;
newnode->leftChild = root->leftChild;
root->leftChild = NULL;
} else {
newnode->leftChild = root;
newnode->rightChild = root->rightChild;
root->rightChild = NULL;
}
return newnode;
}
struct node* deletenode(struct node* root, int data){
struct node* temp;
if (root == NULL)
return NULL;
root = splay(root, data);
if (data != root->data)
return root;
if (!root->leftChild) {
temp = root;
root = root->rightChild;
} else {
temp = root;
root = splay(root->leftChild, data);
root->rightChild = temp->rightChild;
}
free(temp);
return root;
}
void printTree(struct node *root){
if (root == NULL)
return;
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct node* root = newNode(34);
root->leftChild = newNode(15);
root->rightChild = newNode(40);
printf("The Splay tree is \n");
printTree(root);
root = deletenode(root, 40);
printf("\nThe Splay tree after deletion is \n");
printTree(root);
return 0;
}
Output
The Splay tree is 15 34 40 The Splay tree after deletion is 15 34
import java.io.*;
public class SplayTree {
static class node {
int data;
node leftChild, rightChild;
};
static node newNode(int data) {
node Node = new node();
Node.data = data;
Node.leftChild = Node.rightChild = null;
return (Node);
}
static node rightRotate(node x) {
node y = x.leftChild;
x.leftChild = y.rightChild;
y.rightChild = x;
return y;
}
static node leftRotate(node x) {
node y = x.rightChild;
x.rightChild = y.leftChild;
y.leftChild = x;
return y;
}
static node splay(node root, int data) {
if (root == null || root.data == data)
return root;
if (root.data > data) {
if (root.leftChild == null) return root;
if (root.leftChild.data > data) {
root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
root = rightRotate(root);
} else if (root.leftChild.data < data) {
root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
if (root.leftChild.rightChild != null)
root.leftChild = leftRotate(root.leftChild);
}
return (root.leftChild == null)? root: rightRotate(root);
} else {
if (root.rightChild == null) return root;
if (root.rightChild.data > data) {
root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
if (root.rightChild.leftChild != null)
root.rightChild = rightRotate(root.rightChild);
} else if (root.rightChild.data < data) {
root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
root = leftRotate(root);
}
return (root.rightChild == null)? root: leftRotate(root);
}
}
static node insert(node root, int k) {
if (root == null) return newNode(k);
root = splay(root, k);
if (root.data == k) return root;
node newnode = newNode(k);
if (root.data > k) {
newnode.rightChild = root;
newnode.leftChild = root.leftChild;
root.leftChild = null;
} else {
newnode.leftChild = root;
newnode.rightChild = root.rightChild;
root.rightChild = null;
}
return newnode;
}
static node deletenode(node root, int data) {
node temp;
if (root == null)
return null;
root = splay(root, data);
if (data != root.data)
return root;
if (root.leftChild == null) {
temp = root;
root = root.rightChild;
} else {
temp = root;
root = splay(root.leftChild, data);
root.rightChild = temp.rightChild;
}
return root;
}
static void printTree(node root) {
if (root == null)
return;
if (root != null) {
printTree(root.leftChild);
System.out.print(root.data + " ");
printTree(root.rightChild);
}
}
public static void main(String args[]) {
node root = newNode(34);
root.leftChild = newNode(15);
root.rightChild = newNode(40);
System.out.println("The Splay tree is: ");
printTree(root);
root = deletenode(root, 40);
System.out.println("\nThe Splay tree after deletion is: ");
printTree(root);
}
}
Output
The Splay tree is: 15 34 40 The Splay tree after deletion is: 15 34
#Python Code for Deletion operation of Splay Trees
class Node:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild = None
def newNode(data):
node = Node(data)
return node
def rightRotate(x):
y = x.leftChild
x.leftChild = y.rightChild
y.rightChild = x
return y
def leftRotate(x):
y = x.rightChild
x.rightChild = y.leftChild
y.leftChild = x
return y
def splay(root, data):
if root is None or root.data == data:
return root
if root.data > data:
if root.leftChild is None:
return root
if root.leftChild.data > data:
root.leftChild.leftChild = splay(root.leftChild.leftChild, data)
root = rightRotate(root)
elif root.leftChild.data < data:
root.leftChild.rightChild = splay(root.leftChild.rightChild, data)
if root.leftChild.rightChild is not None:
root.leftChild = leftRotate(root.leftChild)
return root if root.leftChild is None else rightRotate(root)
else:
if root.rightChild is None:
return root
if root.rightChild.data > data:
root.rightChild.leftChild = splay(root.rightChild.leftChild, data)
if root.rightChild.leftChild is not None:
root.rightChild = rightRotate(root.rightChild)
elif root.rightChild.data < data:
root.rightChild.rightChild = splay(root.rightChild.rightChild, data)
root = leftRotate(root)
return root if root.rightChild is None else leftRotate(root)
def insert(root, k):
if root is None:
return newNode(k)
root = splay(root, k)
if root.data == k:
return root
newnode = newNode(k)
if root.data > k:
newnode.rightChild = root
newnode.leftChild = root.leftChild
root.leftChild = None
else:
newnode.leftChild = root
newnode.rightChild = root.rightChild
root.rightChild = None
return newnode
def deletenode(root, data):
temp = None
if root is None:
return None
root = splay(root, data)
if data != root.data:
return root
if root.leftChild is None:
temp = root
root = root.rightChild
else:
temp = root
root = splay(root.leftChild, data)
root.rightChild = temp.rightChild
del temp
return root
def printTree(root):
if root is None:
return
if root is not None:
printTree(root.leftChild)
print(root.data, end=" ")
printTree(root.rightChild)
root = newNode(34)
root.leftChild = newNode(15)
root.rightChild = newNode(40)
print("The Splay tree is:")
printTree(root)
root = deletenode(root, 40)
print("\nThe Splay tree after deletion is:")
printTree(root)
Output
The Splay tree is: 15 34 40 The Splay tree after deletion is: 15 34
Search
The search operation in a Splay tree follows the same procedure of the Binary Search Tree operation. However, after the searching is done and the element is found, splaying is applied on the node searched. If the element is not found, then unsuccessful search is prompted.
Example
Following are the implementations of this operation in various programming languages −
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *leftChild, *rightChild;
};
struct node* newNode(int data){
struct node* Node = (struct node*)malloc(sizeof(struct node));
Node->data = data;
Node->leftChild = Node->rightChild = NULL;
return (Node);
}
struct node* rightRotate(struct node *x){
struct node *y = x->leftChild;
x->leftChild = y->rightChild;
y->rightChild = x;
return y;
}
struct node* leftRotate(struct node *x){
struct node *y = x->rightChild;
x->rightChild = y->leftChild;
y->leftChild = x;
return y;
}
struct node* splay(struct node *root, int data){
if (root == NULL || root->data == data)
return root;
if (root->data > data) {
if (root->leftChild == NULL) return root;
if (root->leftChild->data > data) {
root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
root = rightRotate(root);
} else if (root->leftChild->data < data) {
root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
if (root->leftChild->rightChild != NULL)
root->leftChild = leftRotate(root->leftChild);
}
return (root->leftChild == NULL)? root: rightRotate(root);
} else {
if (root->rightChild == NULL) return root;
if (root->rightChild->data > data) {
root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
if (root->rightChild->leftChild != NULL)
root->rightChild = rightRotate(root->rightChild);
} else if (root->rightChild->data < data) {
root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
root = leftRotate(root);
}
return (root->rightChild == NULL)? root: leftRotate(root);
}
}
struct node* insert(struct node *root, int k){
if (root == NULL) return newNode(k);
root = splay(root, k);
if (root->data == k) return root;
struct node *newnode = newNode(k);
if (root->data > k) {
newnode->rightChild = root;
newnode->leftChild = root->leftChild;
root->leftChild = NULL;
} else {
newnode->leftChild = root;
newnode->rightChild = root->rightChild;
root->rightChild = NULL;
}
return newnode;
}
struct node* deletenode(struct node* root, int data){
struct node* temp;
if (root == NULL)
return NULL;
root = splay(root, data);
if (data != root->data)
return root;
if (!root->leftChild) {
temp = root;
root = root->rightChild;
} else {
temp = root;
root = splay(root->leftChild, data);
root->rightChild = temp->rightChild;
}
free(temp);
return root;
}
void printTree(struct node *root){
if (root == NULL)
return;
if (root != NULL) {
printTree(root->leftChild);
printf("%d ", root->data);
printTree(root->rightChild);
}
}
int main(){
struct node* root = newNode(34);
root->leftChild = newNode(15);
root->rightChild = newNode(40);
root->leftChild->leftChild = newNode(12);
root->leftChild->leftChild->rightChild = newNode(14);
root->rightChild->rightChild = newNode(59);
printf("The Splay tree is \n");
printTree(root);
root = deletenode(root, 40);
printf("\nThe Splay tree after deletion is \n");
printTree(root);
return 0;
}
Output
The Splay tree is 12 14 15 34 40 59 The Splay tree after deletion is 12 14 15 34 59
#include <bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node *leftChild, *rightChild;
};
node* newNode(int data){
node* Node = new node();
Node->data = data;
Node->leftChild = Node->rightChild = NULL;
return (Node);
}
node *rightRotate(node *x){
node *y = x->leftChild;
x->leftChild = y->rightChild;
y->rightChild = x;
return y;
}
node *leftRotate(node *x){
node *y = x->rightChild;
x->rightChild = y->leftChild;
y->leftChild = x;
return y;
}
node *splay(node *root, int data){
if (root == NULL || root->data == data)
return root;
if (root->data > data) {
if (root->leftChild == NULL) return root;
if (root->leftChild->data > data) {
root->leftChild->leftChild = splay(root->leftChild->leftChild, data);
root = rightRotate(root);
} else if (root->leftChild->data < data) {
root->leftChild->rightChild = splay(root->leftChild->rightChild, data);
if (root->leftChild->rightChild != NULL)
root->leftChild = leftRotate(root->leftChild);
}
return (root->leftChild == NULL)? root: rightRotate(root);
} else {
if (root->rightChild == NULL) return root;
if (root->rightChild->data > data) {
root->rightChild->leftChild = splay(root->rightChild->leftChild, data);
if (root->rightChild->leftChild != NULL)
root->rightChild = rightRotate(root->rightChild);
} else if (root->rightChild->data < data) {
root->rightChild->rightChild = splay(root->rightChild->rightChild, data);
root = leftRotate(root);
}
return (root->rightChild == NULL)? root: leftRotate(root);
}
}
node* insert(node *root, int k)
{
if (root == NULL) return newNode(k);
root = splay(root, k);
if (root->data == k) return root;
node *newnode = newNode(k);
if (root->data > k) {
newnode->rightChild = root;
newnode->leftChild = root->leftChild;
root->leftChild = NULL;
} else {
newnode->leftChild = root;
newnode->rightChild = root->rightChild;
root->rightChild = NULL;
}
return newnode;
}
node* deletenode(struct node* root, int data){
struct node* temp;
if (root == NULL)
return NULL;
root = splay(root, data);
if (data != root->data)
return root;
if (!root->leftChild) {
temp = root;
root = root->rightChild;
} else {
temp = root;
root = splay(root->leftChild, data);
root->rightChild = temp->rightChild;
}
free(temp);
return root;
}
void printTree(node *root){
if (root == NULL)
return;
if (root != NULL) {
printTree(root->leftChild);
cout<<root->data<<" ";
printTree(root->rightChild);
}
}
int main(){
node* root = newNode(34);
root->leftChild = newNode(15);
root->rightChild = newNode(40);
root->leftChild->leftChild = newNode(12);
root->leftChild->leftChild->rightChild = newNode(14);
root->rightChild->rightChild = newNode(59);
cout<<"The Splay tree is \n";
printTree(root);
root = deletenode(root, 40);
cout<<"\nThe Splay tree after deletion is \n";
printTree(root);
return 0;
}
Output
The Splay tree is 12 14 15 34 40 59 The Splay tree after deletion is 12 14 15 34 59
import java.io.*;
public class SplayTree {
static class node {
int data;
node leftChild, rightChild;
};
static node newNode(int data) {
node Node = new node();
Node.data = data;
Node.leftChild = Node.rightChild = null;
return (Node);
}
static node rightRotate(node x) {
node y = x.leftChild;
x.leftChild = y.rightChild;
y.rightChild = x;
return y;
}
static node leftRotate(node x) {
node y = x.rightChild;
x.rightChild = y.leftChild;
y.leftChild = x;
return y;
}
static node splay(node root, int data) {
if (root == null || root.data == data)
return root;
if (root.data > data) {
if (root.leftChild == null) return root;
if (root.leftChild.data > data) {
root.leftChild.leftChild = splay(root.leftChild.leftChild, data);
root = rightRotate(root);
} else if (root.leftChild.data < data) {
root.leftChild.rightChild = splay(root.leftChild.rightChild, data);
if (root.leftChild.rightChild != null)
root.leftChild = leftRotate(root.leftChild);
}
return (root.leftChild == null)? root: rightRotate(root);
} else {
if (root.rightChild == null) return root;
if (root.rightChild.data > data) {
root.rightChild.leftChild = splay(root.rightChild.leftChild, data);
if (root.rightChild.leftChild != null)
root.rightChild = rightRotate(root.rightChild);
} else if (root.rightChild.data < data) {
root.rightChild.rightChild = splay(root.rightChild.rightChild, data);
root = leftRotate(root);
}
return (root.rightChild == null)? root: leftRotate(root);
}
}
static node insert(node root, int k) {
if (root == null) return newNode(k);
root = splay(root, k);
if (root.data == k) return root;
node newnode = newNode(k);
if (root.data > k) {
newnode.rightChild = root;
newnode.leftChild = root.leftChild;
root.leftChild = null;
} else {
newnode.leftChild = root;
newnode.rightChild = root.rightChild;
root.rightChild = null;
}
return newnode;
}
static node deletenode(node root, int data) {
node temp;
if (root == null)
return null;
root = splay(root, data);
if (data != root.data)
return root;
if (root.leftChild == null) {
temp = root;
root = root.rightChild;
} else {
temp = root;
root = splay(root.leftChild, data);
root.rightChild = temp.rightChild;
}
return root;
}
static void printTree(node root) {
if (root == null)
return;
if (root != null) {
printTree(root.leftChild);
System.out.print(root.data + " ");
printTree(root.rightChild);
}
}
public static void main(String args[]) {
node root = newNode(34);
root.leftChild = newNode(15);
root.rightChild = newNode(40);
root.leftChild.leftChild = newNode(12);
root.leftChild.leftChild.rightChild = newNode(14);
root.rightChild.rightChild = newNode(59);
System.out.println("The Splay tree is: ");
printTree(root);
root = deletenode(root, 40);
System.out.println("\nThe Splay tree after deletion is: ");
printTree(root);
}
}
Output
The Splay tree is: 12 14 15 34 40 59 The Splay tree after deletion is: 12 14 15 34 59
#Python Code for Search Operation of splay Trees
class Node:
def __init__(self, data):
self.data = data
self.leftChild = None
self.rightChild = None
def newNode(data):
newNode = Node(data)
newNode.leftChild = newNode.rightChild = None
return newNode
def rightRotate(x):
y = x.leftChild
x.leftChild = y.rightChild
y.rightChild = x
return y
def leftRotate(x):
y = x.rightChild
x.rightChild = y.leftChild
y.leftChild = x
return y
def splay(root, data):
if root is None or root.data == data:
return root
if root.data > data:
if root.leftChild is None:
return root
if root.leftChild.data > data:
root.leftChild.leftChild = splay(root.leftChild.leftChild, data)
root = rightRotate(root)
elif root.leftChild.data < data:
root.leftChild.rightChild = splay(root.leftChild.rightChild, data)
if root.leftChild.rightChild is not None:
root.leftChild = leftRotate(root.leftChild)
return root if root.leftChild is None else rightRotate(root)
else:
if root.rightChild is None:
return root
if root.rightChild.data > data:
root.rightChild.leftChild = splay(root.rightChild.leftChild, data)
if root.rightChild.leftChild is not None:
root.rightChild = rightRotate(root.rightChild)
elif root.rightChild.data < data:
root.rightChild.rightChild = splay(root.rightChild.rightChild, data)
root = leftRotate(root)
return root if root.rightChild is None else leftRotate(root)
def insert(root, k):
if root is None:
return newNode(k)
root = splay(root, k)
if root.data == k:
return root
newnode = newNode(k)
if root.data > k:
newnode.rightChild = root
newnode.leftChild = root.leftChild
root.leftChild = None
else:
newnode.leftChild = root
newnode.rightChild = root.rightChild
root.rightChild = None
return newnode
def deletenode(root, data):
temp = None
if root is None:
return None
root = splay(root, data)
if data != root.data:
return root
if root.leftChild is None:
temp = root
root = root.rightChild
else:
temp = root
root = splay(root.leftChild, data)
root.rightChild = temp.rightChild
del temp
return root
def printTree(root):
if root is None:
return
if root is not None:
printTree(root.leftChild)
print(root.data, end=" ")
printTree(root.rightChild)
root = newNode(34)
root.leftChild = newNode(15)
root.rightChild = newNode(40)
root.leftChild.leftChild = newNode(12)
root.leftChild.leftChild.rightChild = newNode(14)
root.rightChild.rightChild = newNode(59)
print("The Splay tree is")
printTree(root)
root = deletenode(root, 40)
print("\nThe Splay tree after deletion is")
printTree(root)
Output
The Splay tree is 12 14 15 34 40 59 The Splay tree after deletion is 12 14 15 34 59
Tries Data Structure
A trie is a type of a multi-way search tree, which is fundamentally used to retrieve specific keys from a string or a set of strings. It stores the data in an ordered efficient way since it uses pointers to every letter within the alphabet.
The trie data structure works based on the common prefixes of strings. The root node can have any number of nodes considering the amount of strings present in the set. The root of a trie does not contain any value except the pointers to its child nodes.
There are three types of trie data structures −
Standard Tries
Compressed Tries
Suffix Tries
The real-world applications of trie include − autocorrect, text prediction, sentiment analysis and data sciences.
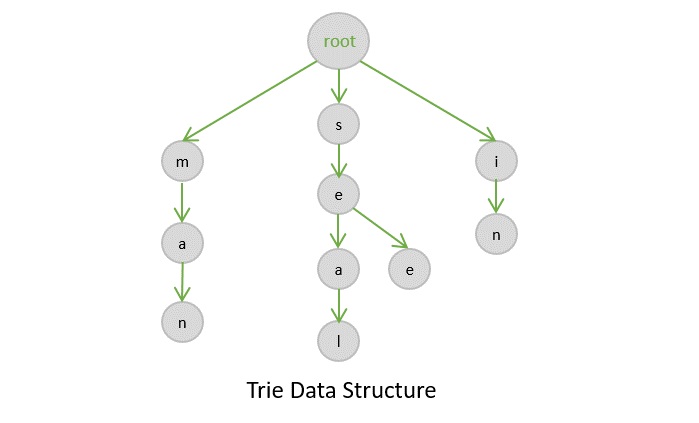
Basic Operations in Tries
The trie data structures also perform the same operations that tree data structures perform. They are −
Insertion
Deletion
Search
Insertion
The insertion operation in a trie is a simple approach. The root in a trie does not hold any value and the insertion starts from the immediate child nodes of the root, which act like a key to their child nodes. However, we observe that each node in a trie represents a singlecharacter in the input string. Hence the characters are added into the tries one by one while the links in the trie act as pointers to the next level nodes.
Example
//C code for insertion operation of tries algorithm
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ALPHABET_SIZE 26
struct TrieNode {
struct TrieNode* children[ALPHABET_SIZE];
bool isEndOfWord;
};
struct TrieNode* createNode() {
struct TrieNode* node = (struct TrieNode*)malloc(sizeof(struct TrieNode));
node->isEndOfWord = false;
for (int i = 0; i < ALPHABET_SIZE; i++) {
node->children[i] = NULL;
}
return node;
}
void insert(struct TrieNode* root, char* word) {
struct TrieNode* curr = root;
for (int i = 0; word[i] != '\0'; i++) {
int index = word[i] - 'a';
if (curr->children[index] == NULL) {
curr->children[index] = createNode();
}
curr = curr->children[index];
}
curr->isEndOfWord = true;
}
bool search(struct TrieNode* root, char* word) {
struct TrieNode* curr = root;
for (int i = 0; word[i] != '\0'; i++) {
int index = word[i] - 'a';
if (curr->children[index] == NULL) {
return false;
}
curr = curr->children[index];
}
return (curr != NULL && curr->isEndOfWord);
}
bool startsWith(struct TrieNode* root, char* prefix) {
struct TrieNode* curr = root;
for (int i = 0; prefix[i] != '\0'; i++) {
int index = prefix[i] - 'a';
if (curr->children[index] == NULL) {
return false;
}
curr = curr->children[index];
}
return true;
}
int main() {
struct TrieNode* root = createNode();
//inserting the elements
insert(root, "Lamborghini");
insert(root, "Mercedes-Benz");
insert(root, "Land Rover");
insert(root, "Maruti Suzuki");
//printing the elements
printf("Inserted values are: \n");
printf("Lamborghini\n");
printf( "Mercedes-Benz\n");
printf( "Land Rover\n");
printf( "Maruti Suzuki");
return 0;
}
Output
Inserted values are: Lamborghini Mercedes-Benz Land Rover Maruti Suzuki
// C++ code for Insertion operation of tries algorithm
#include <iostream>
#include <unordered_map>
using namespace std;
class TrieNode
{
public:
unordered_map<char, TrieNode*> children;
bool isEndOfWord;
TrieNode()
{
isEndOfWord = false;
}
};
class Trie
{
private:
TrieNode* root;
public:
Trie()
{
root = new TrieNode();
}
void insert(string word)
{
TrieNode* curr = root;
for (char ch : word) {
if (curr->children.find(ch) == curr->children.end()) {
curr->children[ch] = new TrieNode();
}
curr = curr->children[ch];
}
curr->isEndOfWord = true;
}
bool search(string word)
{
TrieNode* curr = root;
for (char ch : word) {
if (curr->children.find(ch) == curr->children.end()) {
return false;
}
curr = curr->children[ch];
}
return curr->isEndOfWord;
}
bool startsWith(string prefix)
{
TrieNode* curr = root;
for (char ch : prefix) {
if (curr->children.find(ch) == curr->children.end()) {
return false;
}
curr = curr->children[ch];
}
return true;
}
};
int main()
{
Trie car;
//inserting the elements
car.insert("Lamborghini");
car.insert("Mercedes-Benz");
car.insert("Land Rover");
car.insert("Maruti Suzuki");
//printing the elmenents
printf("Inserted values are: \n");
cout << "Lamborghini" << endl;
cout <<"Mercedes-Benz"<< endl;
cout <<"Land Rover" << endl;
cout << "Maruti Suzuki" << endl;
return 0;
}
Output
Inserted values are: Lamborghini Mercedes-Benz Land Rover Maruti Suzuki
//Java Code for insertion operation of tries Algorithm
import java.util.HashMap;
import java.util.Map;
class TrieNode {
Map<Character, TrieNode> children;
boolean isEndOfWord;
TrieNode() {
children = new HashMap<>();
isEndOfWord = false;
}
}
class Trie {
private TrieNode root;
Trie() {
root = new TrieNode();
}
void insert(String word) {
TrieNode curr = root;
for (char ch : word.toCharArray()) {
curr.children.putIfAbsent(ch, new TrieNode());
curr = curr.children.get(ch);
}
curr.isEndOfWord = true;
}
boolean search(String word) {
TrieNode curr = root;
for (char ch : word.toCharArray()) {
if (!curr.children.containsKey(ch)) {
return false;
}
curr = curr.children.get(ch);
}
return curr.isEndOfWord;
}
boolean startsWith(String prefix) {
TrieNode curr = root;
for (char ch : prefix.toCharArray()) {
if (!curr.children.containsKey(ch)) {
return false;
}
curr = curr.children.get(ch);
}
return true;
}
}
public class Main {
public static void main(String[] args) {
Trie car = new Trie();
//Inserting the elements
car.insert("Lamborghini");
car.insert("Mercedes-Benz");
car.insert("Land Rover");
car.insert("Maruti Suzuki");
//Printing the elements
System.out.println("Inserted values are: ");
System.out.println("Lamborghini");
System.out.println("Mercedes-Benz");
System.out.println("Land Rover");
System.out.println("Maruti Suzuki");
}
}
Output
Inserted values are: Lamborghini Mercedes-Benz Land Rover Maruti Suzuki
#Python Code for insertion operation of tries Algorithm
class TrieNode:
def __init__(self):
self.children = {}
self.isEndOfWord = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
curr = self.root
for ch in word:
if ch not in curr.children:
curr.children[ch] = TrieNode()
curr = curr.children[ch]
curr.isEndOfWord = True
def search(self, word):
curr = self.root
for ch in word:
if ch not in curr.children:
return False
curr = curr.children[ch]
return curr.isEndOfWord
def startsWith(self, prefix):
curr = self.root
for ch in prefix:
if ch not in curr.children:
return False
curr = curr.children[ch]
return True
if __name__ == '__main__':
car = Trie()
#inserting the elements
car.insert("Lamborghini")
car.insert("Mercedes-Benz")
car.insert("Land Rover")
car.insert("Maruti Suzuki")
#printing the elements
print("Inserted values are: ")
print("Lamborghini")
print("Mercedes-Benz")
print("Land Rover")
print("Maruti Suzuki")
Output
Inserted values are: Lamborghini Mercedes-Benz Land Rover Maruti Suzuki
Deletion
The deletion operation in a trie is performed using the bottom-up approach. The element is searched for in a trie and deleted, if found. However, there are some special scenarios that need to be kept in mind while performing the deletion operation.
Case 1 − The key is unique − in this case, the entire key path is deleted from the node. (Unique key suggests that there is no other path that branches out from one path).
Case 2 − The key is not unique − the leaf nodes are updated. For example, if the key to be deleted is see but it is a prefix of another key seethe; we delete the see and change the Boolean values of t, h and e as false.
Case 3 − The key to be deleted already has a prefix − the values until the prefix are deleted and the prefix remains in the tree. For example, if the key to be deleted is heart but there is another key present he; so we delete a, r, and t until only he remains.
Example
//C code for Deletion Operation of tries Algorithm
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
//Define size 26
#define ALPHABET_SIZE 26
struct TrieNode {
struct TrieNode* children[ALPHABET_SIZE];
bool isEndOfWord;
};
struct TrieNode* createNode() {
struct TrieNode* node = (struct TrieNode*)malloc(sizeof(struct TrieNode));
node->isEndOfWord = false;
for (int i = 0; i < ALPHABET_SIZE; i++) {
node->children[i] = NULL;
}
return node;
}
void insert(struct TrieNode* root, char* word) {
struct TrieNode* curr = root;
for (int i = 0; word[i] != '\0'; i++) {
int index = word[i] - 'a';
if (curr->children[index] == NULL) {
curr->children[index] = createNode();
}
curr = curr->children[index];
}
curr->isEndOfWord = true;
}
bool search(struct TrieNode* root, char* word) {
struct TrieNode* curr = root;
for (int i = 0; word[i] != '\0'; i++) {
int index = word[i] - 'a';
if (curr->children[index] == NULL) {
return false;
}
curr = curr->children[index];
}
return (curr != NULL && curr->isEndOfWord);
}
bool startsWith(struct TrieNode* root, char* prefix) {
struct TrieNode* curr = root;
for (int i = 0; prefix[i] != '\0'; i++) {
int index = prefix[i] - 'a';
if (curr->children[index] == NULL) {
return false;
}
curr = curr->children[index];
}
return true;
}
bool deleteWord(struct TrieNode* root, char* word) {
struct TrieNode* curr = root;
struct TrieNode* parent = NULL;
int index;
for (int i = 0; word[i] != '\0'; i++) {
index = word[i] - 'a';
if (curr->children[index] == NULL) {
return false; // Word does not exist in the Trie
}
parent = curr;
curr = curr->children[index];
}
if (!curr->isEndOfWord) {
return false; // Word does not exist in the Trie
}
curr->isEndOfWord = false; // Mark as deleted
if (parent != NULL) {
parent->children[index] = NULL; // Remove the child node
}
return true;
}
int main() {
struct TrieNode* root = createNode();
//Inserting the elements
insert(root, "lamborghini");
insert(root, "mercedes-benz");
insert(root, "land rover");
insert(root, "maruti suzuki");
//Before Deletion
printf("Before Deletion\n");
printf("%d\n", search(root, "lamborghini")); // Output: 1 (true)
printf("%d\n", search(root, "mercedes-benz")); // Output: 1 (true)
printf("%d\n", search(root, "land rover")); // Output: 1 (true)
printf("%d\n", search(root, "maruti suzuki")); // Output: 1 (true)
//Deleting the elements
deleteWord(root, "lamborghini");
deleteWord(root, "land rover");
//After Deletion
printf("After Deletion\n");
printf("%d\n", search(root, "lamborghini")); // Output: 0 (false)
printf("%d\n", search(root, "mercedes-benz")); // Output: 1 (true)
printf("%d\n", search(root, "land rover")); // Output: 0 (false)
printf("%d\n", search(root, "maruti suzuki")); // Output: 1 (true)
return 0;
}
Output
Before Deletion 1 1 1 1 After Deletion 0 1 0 1
//C++ code for Deletion operation of tries algorithm
#include <iostream>
#include <unordered_map>
using namespace std;
class TrieNode {
public:
unordered_map<char, TrieNode*> children;
bool isEndOfWord;
TrieNode() {
isEndOfWord = false;
}
};
class Trie {
private:
TrieNode* root;
public:
Trie() {
root = new TrieNode();
}
void insert(string word) {
TrieNode* curr = root;
for (char ch : word) {
if (curr->children.find(ch) == curr->children.end()) {
curr->children[ch] = new TrieNode();
}
curr = curr->children[ch];
}
curr->isEndOfWord = true;
}
bool search(string word) {
TrieNode* curr = root;
for (char ch : word) {
if (curr->children.find(ch) == curr->children.end()) {
return false;
}
curr = curr->children[ch];
}
return curr->isEndOfWord;
}
bool startsWith(string prefix) {
TrieNode* curr = root;
for (char ch : prefix) {
if (curr->children.find(ch) == curr->children.end()) {
return false;
}
curr = curr->children[ch];
}
return true;
}
bool deleteWord(string word) {
return deleteHelper(root, word, 0);
}
private:
bool deleteHelper(TrieNode* curr, string word, int index) {
if (index == word.length()) {
if (!curr->isEndOfWord) {
return false; // Word does not exist in the Trie
}
curr->isEndOfWord = false; // Mark as deleted
return curr->children.empty(); // Return true if no more children
}
char ch = word[index];
if (curr->children.find(ch) == curr->children.end()) {
return false; // Word does not exist in the Trie
}
TrieNode* child = curr->children[ch];
bool shouldDeleteChild = deleteHelper(child, word, index + 1);
if (shouldDeleteChild) {
curr->children.erase(ch); // Remove the child node if necessary
return curr->children.empty(); // Return true if no more children
}
return false;
}
};
int main() {
Trie car;
//inserting the elemnets
car.insert("Lamborghini");
car.insert("Mercedes-Benz");
car.insert("Land Rover");
car.insert("Maruti Suzuki");
//Before Deletion
cout << "Before Deletion" << endl;
cout << car.search("Lamborghini") << endl; // Output: 1 (true)
cout << car.search("Mercedes-Benz") << endl; // Output: 1 (true)
cout << car.search("Land Rover") << endl; // Output: 1 (true)
cout << car.search("Maruti Suzuki") << endl; // Output: 1 (true)
//Deleting elements using deletion operation
car.deleteWord("Lamborghini");
car.deleteWord("Land Rover");
//After Deletion
cout << "After Deletion" << endl;
cout << car.search("Lamborghini") << endl; // Output: 0 (false)
cout << car.search("Mercedes-Benz") << endl; // Output: 1 (true)
cout << car.search("Land Rover") << endl; // Output: 0 (false)
cout << car.search("Maruti Suzuki") << endl; // Output: 1 (true)
return 0;
}
Output
Before Deletion 1 1 1 1 After Deletion 0 1 0 1
//Java code for Deletion operator of tries algotrithm
import java.util.HashMap;
import java.util.Map;
class TrieNode {
Map<Character, TrieNode> children;
boolean isEndOfWord;
TrieNode() {
children = new HashMap<>();
isEndOfWord = false;
}
}
class Trie {
private TrieNode root;
Trie() {
root = new TrieNode();
}
void insert(String word) {
TrieNode curr = root;
for (char ch : word.toCharArray()) {
curr.children.putIfAbsent(ch, new TrieNode());
curr = curr.children.get(ch);
}
curr.isEndOfWord = true;
}
boolean search(String word) {
TrieNode curr = root;
for (char ch : word.toCharArray()) {
if (!curr.children.containsKey(ch)) {
return false;
}
curr = curr.children.get(ch);
}
return curr.isEndOfWord;
}
boolean startsWith(String prefix) {
TrieNode curr = root;
for (char ch : prefix.toCharArray()) {
if (!curr.children.containsKey(ch)) {
return false;
}
curr = curr.children.get(ch);
}
return true;
}
boolean delete(String word) {
return deleteHelper(root, word, 0);
}
private boolean deleteHelper(TrieNode curr, String word, int index) {
if (index == word.length()) {
if (!curr.isEndOfWord) {
return false; // Word does not exist in the Trie
}
curr.isEndOfWord = false; // Mark as deleted
return curr.children.isEmpty(); // Return true if no more children
}
char ch = word.charAt(index);
if (!curr.children.containsKey(ch)) {
return false; // Word does not exist in the Trie
}
TrieNode child = curr.children.get(ch);
boolean shouldDeleteChild = deleteHelper(child, word, index + 1);
if (shouldDeleteChild) {
curr.children.remove(ch); // Remove the child node if necessary
return curr.children.isEmpty(); // Return true if no more children
}
return false;
}
}
public class Main {
public static void main(String[] args) {
Trie car = new Trie();
//Inserting the elements
car.insert("Lamborghini");
car.insert("Mercedes-Benz");
car.insert("Land Rover");
car.insert("Maruti Suzuki");
//Before Deletion
System.out.println("Before Deletion");
//Printing the elements
System.out.println(car.search("Lamborghini")); // Output: true
System.out.println(car.search("Mercedes-Benz")); // Output: true
System.out.println(car.search("Land Rover")); // Output: true
System.out.println(car.search("Maruti Suzuki")); // Output: true
//Deleting the elements using deletion operation
car.delete("Lamborghini");
car.delete("Land Rover");
// After Deletion
System.out.println("After Deletion");
// Prints the elements in the Boolean expression
System.out.println(car.search("Lamborghini")); // Output: false
System.out.println(car.search("Mercedes-Benz")); // Output: true
System.out.println(car.search("Land Rover")); // Output: false
System.out.println(car.search("Maruti Suzuki")); // Output: true
}
}
Output
Before Deletion true true true true After Deletion false true false true
#python Code for Deletion operation of tries algorithm
class TrieNode:
def __init__(self):
self.children = {}
self.isEndOfWord = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
curr = self.root
for ch in word:
if ch not in curr.children:
curr.children[ch] = TrieNode()
curr = curr.children[ch]
curr.isEndOfWord = True
def search(self, word):
curr = self.root
for ch in word:
if ch not in curr.children:
return False
curr = curr.children[ch]
return curr.isEndOfWord
def startsWith(self, prefix):
curr = self.root
for ch in prefix:
if ch not in curr.children:
return False
curr = curr.children[ch]
return True
def delete(self, word):
return self.deleteHelper(self.root, word, 0)
def deleteHelper(self, curr, word, index):
if index == len(word):
if not curr.isEndOfWord:
return False # Word does not exist in the Trie
curr.isEndOfWord = False # Mark as deleted
return len(curr.children) == 0 # Return True if no more children
ch = word[index]
if ch not in curr.children:
return False # Word does not exist in the Trie
child = curr.children[ch]
shouldDeleteChild = self.deleteHelper(child, word, index + 1)
if shouldDeleteChild:
del curr.children[ch] # Remove the child node if necessary
return len(curr.children) == 0 # Return True if no more children
return False
trie = Trie()
#inserting the elements
trie.insert("Lamborghini")
trie.insert("Mercedes-Benz")
trie.insert("Land Rover")
trie.insert("Maruti Suzuki")
#Before Deletion
print("Before Deletion:")
print(trie.search("Lamborghini")) # Output: True
print(trie.search("Mercedes-Benz")) # Output: True
print(trie.search("Land Rover")) # Output: True
print(trie.search("Maruti Suzuki")) # Output: True
#deleting the elements using Deletion operation
trie.delete("Lamborghini")
trie.delete("Land Rover")
#After Deletion
print("After Deletion:")
#print elements
print(trie.search("Lamborghini")) # Output: False
print(trie.search("Mercedes-Benz")) # Output: True
print(trie.search("Land Rover")) # Output: False
print(trie.search("Maruti Suzuki")) # Output: True
Output
Before Deletion: True True True True After Deletion: False True False True
Search
Searching in a trie is a rather straightforward approach. We can only move down the levels of trie based on the key node (the nodes where insertion operation starts at). Searching is done until the end of the path is reached. If the element is found, search is successful; otherwise, search is prompted unsuccessful.
Example
//C program for search operation of tries algorithm
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define ALPHABET_SIZE 26
struct TrieNode {
struct TrieNode* children[ALPHABET_SIZE];
bool isEndOfWord;
};
struct TrieNode* createNode() {
struct TrieNode* node = (struct TrieNode*)malloc(sizeof(struct TrieNode));
node->isEndOfWord = false;
for (int i = 0; i < ALPHABET_SIZE; i++) {
node->children[i] = NULL;
}
return node;
}
void insert(struct TrieNode* root, char* word) {
struct TrieNode* curr = root;
for (int i = 0; word[i] != '\0'; i++) {
int index = word[i] - 'a';
if (curr->children[index] == NULL) {
curr->children[index] = createNode();
}
curr = curr->children[index];
}
curr->isEndOfWord = true;
}
bool search(struct TrieNode* root, char* word) {
struct TrieNode* curr = root;
for (int i = 0; word[i] != '\0'; i++) {
int index = word[i] - 'a';
if (curr->children[index] == NULL) {
return false;
}
curr = curr->children[index];
}
return (curr != NULL && curr->isEndOfWord);
}
bool startsWith(struct TrieNode* root, char* prefix) {
struct TrieNode* curr = root;
for (int i = 0; prefix[i] != '\0'; i++) {
int index = prefix[i] - 'a';
if (curr->children[index] == NULL) {
return false;
}
curr = curr->children[index];
}
return true;
}
int main() {
struct TrieNode* root = createNode();
//inserting the elements
insert(root, "Lamborghini");
insert(root, "Mercedes-Benz");
insert(root, "Land Rover");
insert(root, "Maruti Suzuki");
//Searching elements
printf("Searching Cars\n");
//Printing searched elements
printf("%d\n", search(root, "Lamborghini")); // Output: 1 (true)
printf("%d\n", search(root, "Mercedes-Benz")); // Output: 1 (true)
printf("%d\n", search(root, "Honda")); // Output: 0 (false)
printf("%d\n", search(root, "Land Rover")); // Output: 1 (true)
printf("%d\n", search(root, "BMW")); // Output: 0 (false)
//Searching the elements the name starts with?
printf("Cars name starts with\n");
//Printing the elements
printf("%d\n", startsWith(root, "Lambo")); // Output: 1 (true)
printf("%d\n", startsWith(root, "Hon")); // Output: 0 (false)
printf("%d\n", startsWith(root, "Hy")); // Output: 0 (false)
printf("%d\n", startsWith(root, "Mar")); // Output: 1 (true)
printf("%d\n", startsWith(root, "Land")); // Output: 1 (true)
return 0;
}
Output
Searching Cars 1 1 0 1 0 Cars name starts with 1 0 0 1 1
//C++ code for Search operation of tries algorithm
#include <iostream>
#include <unordered_map>
using namespace std;
class TrieNode {
public:
unordered_map<char, TrieNode*> children;
bool isEndOfWord;
TrieNode() {
isEndOfWord = false;
}
};
class Trie {
private:
TrieNode* root;
public:
Trie() {
root = new TrieNode();
}
void insert(string word) {
TrieNode* curr = root;
for (char ch : word) {
if (curr->children.find(ch) == curr->children.end()) {
curr->children[ch] = new TrieNode();
}
curr = curr->children[ch];
}
curr->isEndOfWord = true;
}
bool search(string word) {
TrieNode* curr = root;
for (char ch : word) {
if (curr->children.find(ch) == curr->children.end()) {
return false;
}
curr = curr->children[ch];
}
return curr->isEndOfWord;
}
bool startsWith(string prefix) {
TrieNode* curr = root;
for (char ch : prefix) {
if (curr->children.find(ch) == curr->children.end()) {
return false;
}
curr = curr->children[ch];
}
return true;
}
};
int main() {
Trie car;
//inserting the elements
car.insert("Lamborghini");
car.insert("Mercedes-Benz");
car.insert("Land Rover");
car.insert("Maruti Suzuki");
//searching elements
cout<< "Searching Cars"<< endl;
// Printing searched elements in Boolean expression
cout << car.search("Lamborghini") << endl; // Output: 1 (true)
cout << car.search("Mercedes-Benz") << endl; // Output: 1 (true)
cout << car.search("Honda") << endl; // Output: 0 (false)
cout << car.search("Land Rover") << endl; // Output: 1 (true)
cout << car.search("BMW") << endl; // Output: 0 (false)
//searching names starts with?
cout<<"cars name starts with" << endl;
//Printing the elements
cout << car.startsWith("Lambo") << endl; // Output: 1 (true)
cout << car.startsWith("Hon") << endl; // Output: 0 (false)
cout << car.startsWith("Hy") << endl; // Output: 0 (false)
cout << car.startsWith("Mar") << endl; // Output: 1 (true)
cout << car.startsWith("Land") << endl; // Output: 1 (true)
return 0;
}
Output
Searching Cars 1 1 0 1 0 cars name starts with 1 0 0 1 1
//Java program for tries Algorithm
import java.util.HashMap;
import java.util.Map;
class TrieNode {
Map<Character, TrieNode> children;
boolean isEndOfWord;
TrieNode() {
children = new HashMap<>();
isEndOfWord = false;
}
}
class Trie {
private TrieNode root;
Trie() {
root = new TrieNode();
}
void insert(String word) {
TrieNode curr = root;
for (char ch : word.toCharArray()) {
curr.children.putIfAbsent(ch, new TrieNode());
curr = curr.children.get(ch);
}
curr.isEndOfWord = true;
}
boolean search(String word) {
TrieNode curr = root;
for (char ch : word.toCharArray()) {
if (!curr.children.containsKey(ch)) {
return false;
}
curr = curr.children.get(ch);
}
return curr.isEndOfWord;
}
boolean startsWith(String prefix) {
TrieNode curr = root;
for (char ch : prefix.toCharArray()) {
if (!curr.children.containsKey(ch)) {
return false;
}
curr = curr.children.get(ch);
}
return true;
}
}
public class Main {
public static void main(String[] args) {
Trie car = new Trie();
//Inserting the elements
car.insert("Lamborghini");
car.insert("Mercedes-Benz");
car.insert("Land Rover");
car.insert("Maruti Suzuki");
//searching the elements
System.out.println("Searching Cars");
//Printing the searched elements
System.out.println(car.search("Lamborghini")); // Output: true
System.out.println(car.search("Mercedes-Benz")); // Output: true
System.out.println(car.search("Honda")); // Output: false
System.out.println(car.search("Land Rover")); // Output: true
System.out.println(car.search("BMW")); // Output: false
//searching the elements name start with?
System.out.println("Cars name starts with");
//Printing the elements
System.out.println(car.startsWith("Lambo")); // Output: true
System.out.println(car.startsWith("Hon")); // Output: false
System.out.println(car.startsWith("Hy")); // Output: false
System.out.println(car.startsWith("Mar")); // Output: true
System.out.println(car.startsWith("Land")); // Output: true
}
}
Output
Searching Cars true true false true false Cars name starts with true false false true true
#Python code for Search operation of tries algorithm
class TrieNode:
def __init__(self):
self.children = {}
self.isEndOfWord = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
curr = self.root
for ch in word:
if ch not in curr.children:
curr.children[ch] = TrieNode()
curr = curr.children[ch]
curr.isEndOfWord = True
def search(self, word):
curr = self.root
for ch in word:
if ch not in curr.children:
return False
curr = curr.children[ch]
return curr.isEndOfWord
def startsWith(self, prefix):
curr = self.root
for ch in prefix:
if ch not in curr.children:
return False
curr = curr.children[ch]
return True
if __name__ == '__main__':
car = Trie()
#Inserting the elements
car.insert("Lamborghini")
car.insert("Mercedes-Benz")
car.insert("Land Rover")
car.insert("Maruti Suzuki")
#Searching elements
print("Searching Cars")
#Printing the searched elements
print(car.search("Lamborghini")) # Output: True
print(car.search("Mercedes-Benz")) # Output: True
print(car.search("Honda")) # Output: False
print(car.search("Land Rover")) # Output: True
print(car.search("BMW")) # Output: False
#printing elements name starts with?
print("Cars name starts with")
print(car.startsWith("Lambo")) # Output: True
print(car.startsWith("Hon")) # Output: False
print(car.startsWith("Hy")) # Output: False
print(car.startsWith("Mar")) # Output: True
print(car.startsWith("Land")) # Output: True
Output
Before Deletion: True True True True After Deletion: False True False True
Heap Data Structure
Heap is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly. If α has child node β then −
key(α) ≥ key(β)
As the value of parent is greater than that of child, this property generates Max Heap. Based on this criteria, a heap can be of two types −
For Input → 35 33 42 10 14 19 27 44 26 31
Min-Heap − Where the value of the root node is less than or equal to either of its children.
Max-Heap − Where the value of the root node is greater than or equal to either of its children.
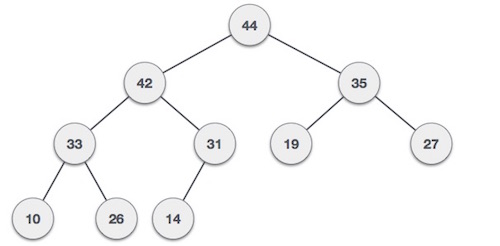
Both trees are constructed using the same input and order of arrival.
Max Heap Construction Algorithm
We shall use the same example to demonstrate how a Max Heap is created. The procedure to create Min Heap is similar but we go for min values instead of max values.
We are going to derive an algorithm for max heap by inserting one element at a time. At any point of time, heap must maintain its property. While insertion, we also assume that we are inserting a node in an already heapified tree.
Step 1 − Create a new node at the end of heap. Step 2 − Assign new value to the node. Step 3 − Compare the value of this child node with its parent. Step 4 − If value of parent is less than child, then swap them. Step 5 − Repeat step 3 & 4 until Heap property holds.
Note − In Min Heap construction algorithm, we expect the value of the parent node to be less than that of the child node.
Let's understand Max Heap construction by an animated illustration. We consider the same input sample that we used earlier.

Example
//C code for Max Heap construction Algorithm
#include <stdio.h>
#include <stdlib.h>
// Structure to represent a heap
typedef struct {
int* array; // Array to store heap elements
int capacity; // Maximum capacity of the heap
int size; // Current size of the heap
} Heap;
// Function to create a new heap
Heap* createHeap(int capacity)
{
Heap* heap = (Heap*)malloc(sizeof(Heap));
heap->array = (int*)malloc(capacity * sizeof(int));
heap->capacity = capacity;
heap->size = 0;
return heap;
}
// Function to swap two elements in the heap
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// Function to heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left < heap->size && heap->array[left] > heap->array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < heap->size && heap->array[right] > heap->array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(&heap->array[i], &heap->array[largest]);
heapify(heap, largest);
}
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
if (heap->size == heap->capacity) {
printf("Heap is full. Cannot insert more elements.\n");
return;
}
// Insert the new element at the end
int i = heap->size++;
heap->array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
swap(&heap->array[i], &heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// Function to extract the maximum element from the heap
int extractMax(Heap* heap)
{
if (heap->size == 0) {
printf("Heap is empty. Cannot extract maximum element.\n");
return -1;
}
// Store the root element
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Heapify the root
heapify(heap, 0);
return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
printf("Heap elements: ");
for (int i = 0; i < heap->size; i++) {
printf("%d ", heap-<array[i]);
}
printf("\n");
}
// Example usage of the heap
int main()
{
Heap* heap = createHeap(10);
insert(heap, 35);
insert(heap, 33);
insert(heap, 42);
insert(heap, 10);
insert(heap, 14);
insert(heap, 19);
insert(heap, 27);
insert(heap, 44);
insert(heap, 26);
insert(heap, 31);
printHeap(heap);
int max = extractMax(heap);
printf("Maximum element: %d\n", max);
return 0;
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44
//C++ code for Max Heap construction Algorithm
#include <iostream>
// Structure to represent a heap
struct Heap {
int* array; // Array to store heap elements
int capacity; // Maximum capacity of the heap
int size; // Current size of the heap
};
// Function to create a new heap
Heap* createHeap(int capacity)
{
Heap* heap = new Heap;
heap->array = new int[capacity];
heap->capacity = capacity;
heap->size = 0;
return heap;
}
// Function to swap two elements in the heap
void swap(int& a, int& b)
{
int temp = a;
a = b;
b = temp;
}
// Function to heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left <heap->size && heap->array[left] > heap->array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right <heap->size && heap->array[right] > heap->array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(heap->array[i], heap->array[largest]);
heapify(heap, largest);
}
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
if (heap->size == heap->capacity) {
std::cout << "Heap is full. Cannot insert more elements." << std::endl;
return;
}
// Insert the new element at the end
int i = heap->size++;
heap->array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
swap(heap->array[i], heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// Function to extract the maximum element from the heap
int extractMax(Heap* heap)
{
if (heap->size == 0) {
std::cout << "Heap is empty. Cannot extract maximum element." << std::endl;
return -1;
}
// Store the root element
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Heapify the root
heapify(heap, 0);
return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
std::cout << "Heap elements: ";
for (int i = 0; i < heap->size; i++) {
std::cout << heap->array[i] << " ";
}
std::cout << std::endl;
}
// Example usage of the heap
int main()
{
Heap* heap = createHeap(10);
insert(heap, 35);
insert(heap, 33);
insert(heap, 42);
insert(heap, 10);
insert(heap, 14);
insert(heap, 19);
insert(heap, 27);
insert(heap, 44);
insert(heap, 26);
insert(heap, 31);
printHeap(heap);
int max = extractMax(heap);
std::cout << "Maximum element: " << max << std::endl;
return 0;
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44
// Java code for for Max Heap construction Algorithm
//Structure to represent a heap
public class MaxHeap {
private int[] heap; // To store heap elements
private int capacity; // Maximum capacity of the heap
private int size; // Current size of the heap
// To create a new heap
public MaxHeap(int capacity) {
this.capacity = capacity;
this.size = 0;
this.heap = new int[capacity];
}
private int parent(int i) {
return (i - 1) / 2;
}
private int leftChild(int i) {
return 2 * i + 1;
}
private int rightChild(int i) {
return 2 * i + 2;
}
private void swap(int i, int j) {
int temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
// Heapify a subtree rooted at index i
private void heapifyDown(int i) {
int largest = i;
int left = leftChild(i);
int right = rightChild(i);
// Check if the left child is larger than the root
if (left < size && heap[left] > heap[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < size && heap[right] > heap[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(i, largest);
heapifyDown(largest);
}
}
private void heapifyUp(int i) {
while (i > 0 && heap[i] > heap[parent(i)]) {
int parent = parent(i);
swap(i, parent);
i = parent;
}
}
// Insert the new element at the end
public void insert(int value) {
if (size == capacity) {
System.out.println("Heap is full. Cannot insert more elements.");
return;
}
heap[size] = value;
size++;
heapifyUp(size - 1);
}
// Function to extract the maximum element from the heap
public int extractMax() {
if (size == 0) {
System.out.println("Heap is empty. Cannot extract maximum element.");
return -1;
}
// store th root element
int max = heap[0];
//Replace the root with the last elements
heap[0] = heap[size - 1];
size--;
heapifyDown(0);
return max;
}
//print the elements of the heap
public void printHeap() {
System.out.print("Heap elements: ");
for (int i = 0; i < size; i++) {
System.out.print(heap[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
MaxHeap heap = new MaxHeap(10);
heap.insert(35);
heap.insert(33);
heap.insert(42);
heap.insert(10);
heap.insert(14);
heap.insert(19);
heap.insert(27);
heap.insert(44);
heap.insert(26);
heap.insert(31);
heap.printHeap();
int max = heap.extractMax();
System.out.println("Maximum element: " + max);
}
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44
# Python code for for Max Heap construction Algorithm
class MaxHeap:
def __init__(self):
self.heap = []
def parent(self, i):
return (i - 1) // 2
def left_child(self, i):
return 2 * i + 1
def right_child(self, i):
return 2 * i + 2
#Function to swap two elements in the heap
def swap(self, i, j):
self.heap[i], self.heap[j] = self.heap[j], self.heap[i]
# Function to heapify a subtree rooted at index i
def heapify_down(self, i):
left = self.left_child(i)
right = self.right_child(i)
largest = i
#Check if the left child is larger than the root
if left < len(self.heap) and self.heap[left] >self.heap[largest]:
largest = left
# Check if the right child is larger than the largest so far
if right < len(self.heap) and self.heap[right] > self.heap[largest]:
largest = right
# If the largest is not the root, swap the root with the largest
if largest != i:
self.swap(i, largest)
self.heapify_down(largest)
def heapify_up(self, i):
while i > 0 and self.heap[i] > self.heap[self.parent(i)]:
parent = self.parent(i)
self.swap(i, parent)
i = parent
# Insert the new element at the end
def insert(self, value):
self.heap.append(value)
# Fix the heap property if it is violated
self.heapify_up(len(self.heap) - 1)
# Function to extract the maximum element from the heap
def extract_max(self):
if len(self.heap) == 0:
print("Heap is empty. Cannot extract maximum element.")
return None
max_value = self.heap[0]
self.heap[0] = self.heap[-1]
self.heap.pop()
self.heapify_down(0)
return max_value
# Function to print the elements of the heap
def print_heap(self):
print("Heap elements:", end=" ")
for value in self.heap:
print(value, end=" ")
print()
# Example usage of the heap
heap = MaxHeap()
heap.insert(35)
heap.insert(33)
heap.insert(42)
heap.insert(10)
heap.insert(14)
heap.insert(19)
heap.insert(27)
heap.insert(44)
heap.insert(26)
heap.insert(31)
heap.print_heap()
max_value = heap.extract_max()
print("Maximum element:", max_value)
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44s
Max Heap Deletion Algorithm
Let us derive an algorithm to delete from max heap. Deletion in Max (or Min) Heap always happens at the root to remove the Maximum (or minimum) value.
Step 1 − Remove root node. Step 2 − Move the last element of last level to root. Step 3 − Compare the value of this child node with its parent. Step 4 − If value of parent is less than child, then swap them. Step 5 − Repeat step 3 & 4 until Heap property holds.
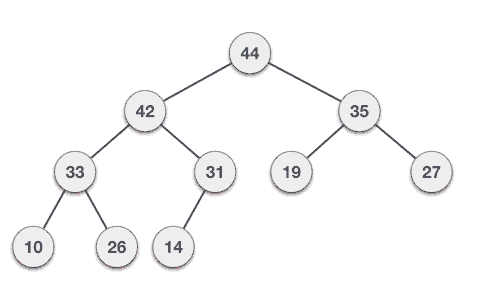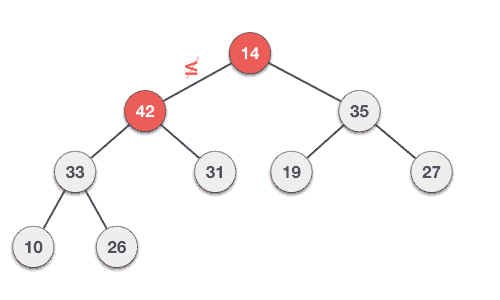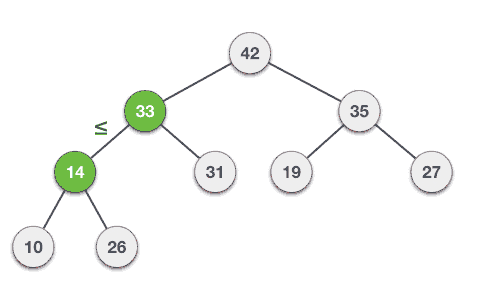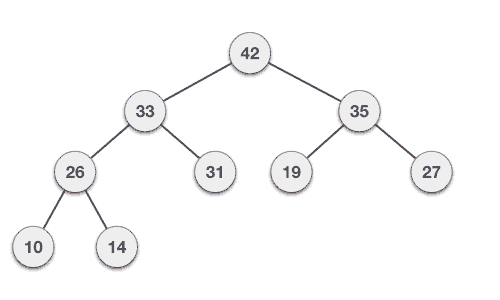
Example
//C code for Max Heap Deletion Algorithm
#include <stdio.h>
#include <stdlib.h>
// Structure to represent a heap
typedef struct {
int* array; // Array to store heap elements
int capacity; // Maximum capacity of the heap
int size; // Current size of the heap
} Heap;
// create a new heap
Heap* createHeap(int capacity)
{
Heap* heap = (Heap*)malloc(sizeof(Heap));
heap->array = (int*)malloc(capacity * sizeof(int));
heap->capacity = capacity;
heap->size = 0;
return heap;
}
// swap two elements in the heap
void swap(int* a, int* b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// Heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left < heap->size && heap->array[left] > heap->array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < heap->size && heap->array[right] > heap->array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(&heap->array[i], &heap->array[largest]);
heapify(heap, largest);
}
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
if (heap->size == heap->capacity) {
printf("Heap is full. Cannot insert more elements.\n");
return;
}
// Insert the new element at the end
int i = heap->size++;
heap->array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
swap(&heap->array[i], &heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// delete the maximum element from the heap
int deleteMax(Heap* heap)
{
if (heap->size == 0) {
printf("Heap is empty. Cannot extract maximum element.\n");
return -1;
}
// Store the root element
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Heapify the root
heapify(heap, 0);
return max;
}
// print the elements of the heap
void printHeap(Heap* heap)
{
printf("Heap elements: ");
for (int i = 0; i < heap->size; i++) {
printf("%d ", heap->array[i]);
}
printf("\n");
}
// Deallocate memory occupied by the heap
void destroyHeap(Heap* heap)
{
free(heap->array);
free(heap);
}
// Example usage of the heap
int main()
{
Heap* heap = createHeap(10);
insert(heap, 35);
insert(heap, 33);
insert(heap, 42);
insert(heap, 10);
insert(heap, 14);
insert(heap, 19);
insert(heap, 27);
insert(heap, 44);
insert(heap, 26);
insert(heap, 31);
printHeap(heap);
// Deleting the maximum element in the heap
int max = deleteMax(heap);
printf("Maximum element: %d\n", max);
printHeap(heap);
destroyHeap(heap);
return 0;
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44 Heap elements: 42 33 35 26 31 19 27 10 14
//C++ code for Max Heap Deletion Algorithm
#include <iostream>
// Structure to represent a heap
struct Heap {
int* array; // Array to store heap elements
int capacity; // Maximum capacity of the heap
int size; // Current size of the heap
};
// Create a new heap
Heap* createHeap(int capacity)
{
Heap* heap = new Heap;
heap->array = new int[capacity];
heap->capacity = capacity;
heap->size = 0;
return heap;
}
// Swap two elements in the heap
void swap(int& a, int& b)
{
int temp = a;
a = b;
b = temp;
}
// Heapify a subtree rooted at index i
void heapify(Heap* heap, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left < heap->size && heap->array[left] > heap->array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < heap->size && heap->array[right] > heap->array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(heap->array[i], heap->array[largest]);
heapify(heap, largest);
}
}
// Function to insert a new element into the heap
void insert(Heap* heap, int value)
{
if (heap->size == heap->capacity) {
std::cout << "Heap is full. Cannot insert more elements." << std::endl;
return;
}
// Insert the new element at the end
int i = heap->size++;
heap->array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && heap->array[(i - 1) / 2] < heap->array[i]) {
swap(heap->array[i], heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// Function to delete the maximum element from the heap
int deleteMax(Heap* heap)
{
if (heap->size == 0) {
std::cout << "Heap is empty. Cannot extract maximum element." << std::endl;
return -1;
}
// Store the root element
int max = heap->array[0];
// Replace the root with the last element
heap->array[0] = heap->array[heap->size - 1];
heap->size--;
// Heapify the root
heapify(heap, 0);
return max;
}
// Function to print the elements of the heap
void printHeap(Heap* heap)
{
std::cout << "Heap elements: ";
for (int i = 0; i < heap->size; i++) {
std::cout << heap->array[i] << " ";
}
std::cout << std::endl;
}
// Function to deallocate memory occupied by the heap
void destroyHeap(Heap* heap)
{
delete[] heap->array;
delete heap;
}
// Example usage of the heap
int main()
{
Heap* heap = createHeap(10);
insert(heap, 35);
insert(heap, 33);
insert(heap, 42);
insert(heap, 10);
insert(heap, 14);
insert(heap, 19);
insert(heap, 27);
insert(heap, 44);
insert(heap, 26);
insert(heap, 31);
printHeap(heap);
int max = deleteMax(heap);
std::cout << "Maximum element: " << max << std::endl;
printHeap(heap);
destroyHeap(heap);
return 0;
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44 Heap elements: 42 33 35 26 31 19 27 10 14
// Java code for for Max Heap Deletion Algorithm
// Structure to represent a heap
class Heap {
private int[] array; // Array to store heap elements
private int capacity; // Maximum capacity of the heap
private int size; // Current size of the heap
// To create a new heap
public Heap(int capacity) {
this.array = new int[capacity];
this.capacity = capacity;
this.size = 0;
}
// Swap two elements in the heap
private void swap(int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}
// Heapify a subtree rooted at index i
private void heapify(int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
// Check if the left child is larger than the root
if (left < size && array[left] > array[largest])
largest = left;
// Check if the right child is larger than the largest so far
if (right < size && array[right] > array[largest])
largest = right;
// If the largest is not the root, swap the root with the largest
if (largest != i) {
swap(i, largest);
heapify(largest);
}
}
// Insert a new element into the heap
public void insert(int value) {
if (size == capacity) {
System.out.println("Heap is full. Cannot insert more elements.");
return;
}
// Insert the new element at the end
int i = size++;
array[i] = value;
// Fix the heap property if it is violated
while (i != 0 && array[(i - 1) / 2] < array[i]) {
swap(i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
// Delete the maximum element from the heap
public int deleteMax() {
if (size == 0) {
System.out.println("Heap is empty. Cannot extract maximum element.");
return -1;
}
// Store the root element
int max = array[0];
// Replace the root with the last element
array[0] = array[size - 1];
size--;
// Heapify the root
heapify(0);
return max;
}
// Print the elements of the heap
public void printHeap() {
System.out.print("Heap elements: ");
for (int i = 0; i < size; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
// Deallocate memory occupied by the heap
public void destroyHeap() {
array = null;
size = 0;
}
}
//Inserting the elements
public class Main {
public static void main(String[] args) {
Heap heap = new Heap(10);
heap.insert(35);
heap.insert(33);
heap.insert(42);
heap.insert(10);
heap.insert(14);
heap.insert(19);
heap.insert(27);
heap.insert(44);
heap.insert(26);
heap.insert(31);
heap.printHeap();
int max = heap.deleteMax();
System.out.println("Maximum element: " + max);
//Printing the heap elements after deletion of max element
heap.printHeap();
heap.destroyHeap();
}
}
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44 Heap elements: 42 33 35 26 31 19 27 10 14
#Python code for Max Heap Deletion Algorithm
class Heap:
def __init__(self, capacity):
self.array = [0] * capacity #array to store heap elements
self.capacity = capacity #maximum capacity of the heap
self.size = 0 #Current size of the heap
# swap two elements in the heap
def swap(self, a, b):
self.array[a], self.array[b] = self.array[b], self.array[a]
# Heapify a subtree rooted at index i
def heapify(self, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
# Check if the left child is larger than the root
if left < self.size and self.array[left] > self.array[largest]:
largest = left
# Check if the right child is larger than the largest so far
if right < self.size and self.array[right] > self.array[largest]:
largest = right
# If the largest is not the root, swap the root with the largest
if largest != i:
self.swap(i, largest)
self.heapify(largest)
# insert a new element into the heap
def insert(self, value):
if self.size == self.capacity:
print("Heap is full. Cannot insert more elements.")
return
# Insert the new element at the end
i = self.size
self.size += 1
self.array[i] = value
# Fix the heap property if it is violated
while i != 0 and self.array[(i - 1) // 2] < self.array[i]:
self.swap(i, (i - 1) // 2)
i = (i - 1) // 2
# delete the maximum element from the heap
def deleteMax(self):
if self.size == 0:
print("Heap is empty. Cannot extract maximum element.")
return -1
# store the root element
max_value = self.array[0]
# Replace the root with the last element
self.array[0] = self.array[self.size - 1]
self.size -= 1
# Heapify the root
self.heapify(0)
return max_value
# print the elements of the heap
def printHeap(self):
print("Heap elements:", end=" ")
for i in range(self.size):
print(self.array[i], end=" ")
print()
# deallocate memory occupied by the heap
def destroyHeap(self):
self.array = []
self.size = 0
# Example usage of the heap
heap = Heap(10)
heap.insert(35)
heap.insert(33)
heap.insert(42)
heap.insert(10)
heap.insert(14)
heap.insert(19)
heap.insert(27)
heap.insert(44)
heap.insert(26)
heap.insert(31)
heap.printHeap()
max_value = heap.deleteMax()
print("Maximum element:", max_value)
heap.printHeap()
heap.destroyHeap()
Output
Heap elements: 44 42 35 33 31 19 27 10 26 14 Maximum element: 44 Heap elements: 42 33 35 26 31 19 27 10 14
Recursion Algorithms
Some computer programming languages allow a module or function to call itself. This technique is known as recursion. In recursion, a function α either calls itself directly or calls a function β that in turn calls the original function α. The function α is called recursive function.
Example − a function calling itself.
int function(int value) {
if(value < 1)
return;
function(value - 1);
printf("%d ",value);
}
Example − a function that calls another function which in turn calls it again.
int function1(int value1) {
if(value1 < 1)
return;
function2(value1 - 1);
printf("%d ",value1);
}
int function2(int value2) {
function1(value2);
}
Properties
A recursive function can go infinite like a loop. To avoid infinite running of recursive function, there are two properties that a recursive function must have −
Base criteria − There must be at least one base criteria or condition, such that, when this condition is met the function stops calling itself recursively.
Progressive approach − The recursive calls should progress in such a way that each time a recursive call is made it comes closer to the base criteria.
Implementation
Many programming languages implement recursion by means of stacks. Generally, whenever a function (caller) calls another function (callee) or itself as callee, the caller function transfers execution control to the callee. This transfer process may also involve some data to be passed from the caller to the callee.
This implies, the caller function has to suspend its execution temporarily and resume later when the execution control returns from the callee function. Here, the caller function needs to start exactly from the point of execution where it puts itself on hold. It also needs the exact same data values it was working on. For this purpose, an activation record (or stack frame) is created for the caller function.
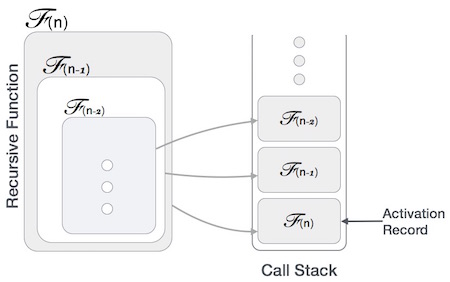
This activation record keeps the information about local variables, formal parameters, return address and all information passed to the caller function.
Analysis of Recursion
One may argue why to use recursion, as the same task can be done with iteration. The first reason is, recursion makes a program more readable and because of latest enhanced CPU systems, recursion is more efficient than iterations.
Time Complexity
In case of iterations, we take number of iterations to count the time complexity. Likewise, in case of recursion, assuming everything is constant, we try to figure out the number of times a recursive call is being made. A call made to a function is Ο(1), hence the (n) number of times a recursive call is made makes the recursive function Ο(n).
Space Complexity
Space complexity is counted as what amount of extra space is required for a module to execute. In case of iterations, the compiler hardly requires any extra space. The compiler keeps updating the values of variables used in the iterations. But in case of recursion, the system needs to store activation record each time a recursive call is made. Hence, it is considered that space complexity of recursive function may go higher than that of a function with iteration.
Example
// C program for Recursion Data Structure
#include <stdio.h>
int factorial(int n) {
// Base case: factorial of 0 is 1
if (n == 0)
return 1;
// Recursive case: multiply n with factorial of (n-1)
return n * factorial(n - 1);
}
int main() {
// case 1
int number = 6;
printf("Number is: %d\n" , 6);
//case 2
if (number < 0) {
printf("Error: Factorial is undefined for negative numbers.\n");
return 1;
}
int result = factorial(number);
//print the output
printf("Factorial of %d is: %d\n", number, result);
return 0;
}
Output
Number is: 6 Factorial of 6 is: 720
// CPP program for Recursion Data Structure
#include <iostream>
int factorial(int n) {
// Base case: factorial of 0 is 1
if (n == 0)
return 1;
// Recursive case: multiply n with factorial of (n-1)
return n * factorial(n - 1);
}
int main() {
// case 1
int number = 6;
std::cout<<"Number is: "<<number<<"\n";
//case 2
if (number < 0) {
std::cout << "Error: Factorial is undefined for negative numbers.\n";
return 1;
}
int result = factorial(number);
//print the output
std::cout << "Factorial of " << number << " is: " << result << std::endl;
return 0;
}
Output
Number is: 6 Factorial of 6 is: 720
// Java program for Recursion Data Structure
import java.util.Scanner;
public class Main {
public static int factorial(int n) {
// Base case: factorial of 0 is 1
if (n == 0)
return 1;
// Recursive case: multiply n with factorial of (n-1)
return n * factorial(n - 1);
}
public static void main(String[] args) {
//Case 1
int number = 6;
System.out.println("Number is: " + number);
//Case 2
if (number < 0) {
System.out.println("Error: Factorial is undefined for negative numbers.");
System.exit(1);
}
int result = factorial(number);
//print the output
System.out.println("Factorial of " + number + " is: " + result);
}
}
Output
Number is: 6 Factorial of 6 is: 720
# Python program for Recursion Data Structure
def factorial(n):
#Base Case: factorial of 0 is 1
if n == 0:
return 1
# Recursive case: multiply n with factorial of (n-1)
return n * factorial(n - 1)
#Case 1:
number = 6;
print("Number is: ", number);
#Case 2:
if number < 0:
print("Error: Factorial is undefined for negative numbers.")
else:
result = factorial(number)
# print the output
print("Factorial of", number, "is: ", result)
Output
Number is: 6 Factorial of 6 is: 720
Tower of Hanoi Using Recursion
Tower of Hanoi, is a mathematical puzzle which consists of three towers (pegs) and more than one rings is as depicted −
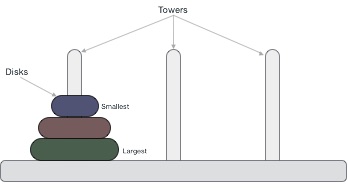
These rings are of different sizes and stacked upon in an ascending order, i.e. the smaller one sits over the larger one. There are other variations of the puzzle where the number of disks increase, but the tower count remains the same.
Rules
The mission is to move all the disks to some another tower without violating the sequence of arrangement. A few rules to be followed for Tower of Hanoi are −
- Only one disk can be moved among the towers at any given time.
- Only the "top" disk can be removed.
- No large disk can sit over a small disk.
Following is an animated representation of solving a Tower of Hanoi puzzle with three disks.
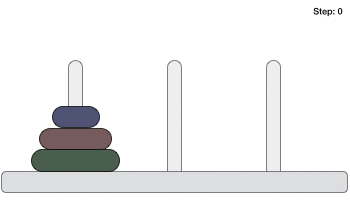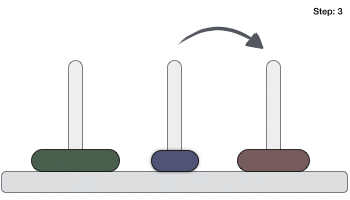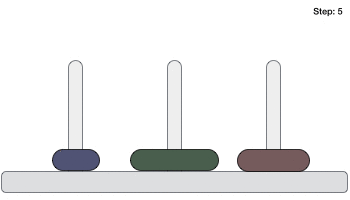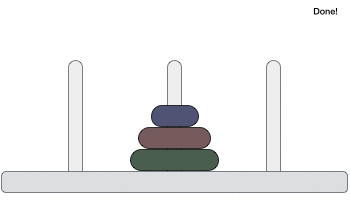
Tower of Hanoi puzzle with n disks can be solved in minimum 2n−1 steps. This presentation shows that a puzzle with 3 disks has taken 23 - 1 = 7 steps.
Algorithm
To write an algorithm for Tower of Hanoi, first we need to learn how to solve this problem with lesser amount of disks, say → 1 or 2. We mark three towers with name, source, destination and aux (only to help moving the disks). If we have only one disk, then it can easily be moved from source to destination peg.
If we have 2 disks −
- First, we move the smaller (top) disk to aux peg.
- Then, we move the larger (bottom) disk to destination peg.
- And finally, we move the smaller disk from aux to destination peg.
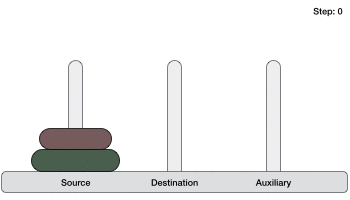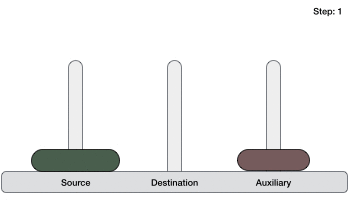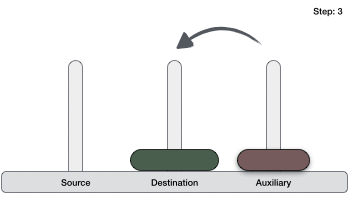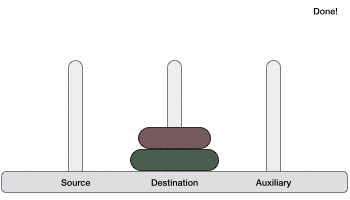
So now, we are in a position to design an algorithm for Tower of Hanoi with more than two disks. We divide the stack of disks in two parts. The largest disk (nth disk) is in one part and all other (n-1) disks are in the second part.
Our ultimate aim is to move disk n from source to destination and then put all other (n1) disks onto it. We can imagine to apply the same in a recursive way for all given set of disks.
The steps to follow are −
Step 1 − Move n-1 disks fromsourcetoauxStep 2 − Move nth disk fromsourcetodestStep 3 − Move n-1 disks fromauxtodest
A recursive algorithm for Tower of Hanoi can be driven as follows −
START
Procedure Hanoi(disk, source, dest, aux)
IF disk == 1, THEN
move disk from source to dest
ELSE
Hanoi(disk - 1, source, aux, dest) // Step 1
move disk from source to dest // Step 2
Hanoi(disk - 1, aux, dest, source) // Step 3
END IF
END Procedure
STOP
Example
#include <stdio.h>
#include <stdbool.h>
#define MAX 10
int list[MAX] = {1,8,4,6,0,3,5,2,7,9};
void display(){
int i;
printf("[");
// navigate through all items
for(i = 0; i < MAX; i++) {
printf("%d ",list[i]);
}
printf("]\n");
}
void bubbleSort() {
int temp;
int i,j;
bool swapped = false;
// loop through all numbers
for(i = 0; i < MAX-1; i++) {
swapped = false;
// loop through numbers falling ahead
for(j = 0; j < MAX-1-i; j++) {
printf("Items compared: [ %d, %d ] ", list[j],list[j+1]);
// check if next number is lesser than current no
// swap the numbers.
// (Bubble up the highest number)
if(list[j] > list[j+1]) {
temp = list[j];
list[j] = list[j+1];
list[j+1] = temp;
swapped = true;
printf(" => swapped [%d, %d]\n",list[j],list[j+1]);
} else {
printf(" => not swapped\n");
}
}
// if no number was swapped that means
// array is sorted now, break the loop.
if(!swapped) {
break;
}
printf("Iteration %d#: ",(i+1));
display();
}
}
int main() {
printf("Input Array: ");
display();
printf("\n");
bubbleSort();
printf("\nOutput Array: ");
display();
}
Output
Input Array: [1 8 4 6 0 3 5 2 7 9 ] Items compared: [ 1, 8 ] => not swapped Items compared: [ 8, 4 ] => swapped [4, 8] Items compared: [ 8, 6 ] => swapped [6, 8] Items compared: [ 8, 0 ] => swapped [0, 8] Items compared: [ 8, 3 ] => swapped [3, 8] Items compared: [ 8, 5 ] => swapped [5, 8] Items compared: [ 8, 2 ] => swapped [2, 8] Items compared: [ 8, 7 ] => swapped [7, 8] Items compared: [ 8, 9 ] => not swapped Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ] Items compared: [ 1, 4 ] => not swapped Items compared: [ 4, 6 ] => not swapped Items compared: [ 6, 0 ] => swapped [0, 6] Items compared: [ 6, 3 ] => swapped [3, 6] Items compared: [ 6, 5 ] => swapped [5, 6] Items compared: [ 6, 2 ] => swapped [2, 6] Items compared: [ 6, 7 ] => not swapped Items compared: [ 7, 8 ] => not swapped Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ] Items compared: [ 1, 4 ] => not swapped Items compared: [ 4, 0 ] => swapped [0, 4] Items compared: [ 4, 3 ] => swapped [3, 4] Items compared: [ 4, 5 ] => not swapped Items compared: [ 5, 2 ] => swapped [2, 5] Items compared: [ 5, 6 ] => not swapped Items compared: [ 6, 7 ] => not swapped Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ] Items compared: [ 1, 0 ] => swapped [0, 1] Items compared: [ 1, 3 ] => not swapped Items compared: [ 3, 4 ] => not swapped Items compared: [ 4, 2 ] => swapped [2, 4] Items compared: [ 4, 5 ] => not swapped Items compared: [ 5, 6 ] => not swapped Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ] Items compared: [ 0, 1 ] => not swapped Items compared: [ 1, 3 ] => not swapped Items compared: [ 3, 2 ] => swapped [2, 3] Items compared: [ 3, 4 ] => not swapped Items compared: [ 4, 5 ] => not swapped Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ] Items compared: [ 0, 1 ] => not swapped Items compared: [ 1, 2 ] => not swapped Items compared: [ 2, 3 ] => not swapped Items compared: [ 3, 4 ] => not swapped Output Array: [0 1 2 3 4 5 6 7 8 9 ]
// C++ Code for Tower of Hanoi
#include <iostream>
#include <array>
#include <algorithm>
const int MAX = 10;
std::array<int, MAX> list = {1, 8, 4, 6, 0, 3, 5, 2, 7, 9};
void display() {
std::cout << "[";
// navigate through all items
for (int i = 0; i < MAX; i++) {
std::cout << list[i] << " ";
}
std::cout << "]\n";
}
void bubbleSort() {
int temp;
bool swapped = false;
// loop through all numbers
for (int i = 0; i < MAX - 1; i++) {
swapped = false;
// loop through numbers falling ahead
for (int j = 0; j < MAX - 1 - i; j++) {
std::cout << "Items compared: [" << list[j] << ", " << list[j+1] << "] ";
// check if next number is lesser than current no
// swap the numbers.
// (Bubble up the highest number)
if (list[j] > list[j+1]) {
std::swap(list[j], list[j+1]);
swapped = true;
std::cout << "=> swapped [" << list[j] << ", " << list[j+1] << "]\n";
} else {
std::cout << "=> not swapped\n";
}
}
// if no number was swapped that means
// array is sorted now, break the loop.
if (!swapped) {
break;
}
std::cout << "Iteration " << (i+1) << "#: ";
display();
}
}
int main() {
std::cout << "Input Array: ";
display();
std::cout << "\n";
bubbleSort();
std::cout << "\nOutput Array: ";
display();
return 0;
}
Output
Input Array: [1 8 4 6 0 3 5 2 7 9 ] Items compared: [1, 8] => not swapped Items compared: [8, 4] => swapped [4, 8] Items compared: [8, 6] => swapped [6, 8] Items compared: [8, 0] => swapped [0, 8] Items compared: [8, 3] => swapped [3, 8] Items compared: [8, 5] => swapped [5, 8] Items compared: [8, 2] => swapped [2, 8] Items compared: [8, 7] => swapped [7, 8] Items compared: [8, 9] => not swapped Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ] Items compared: [1, 4] => not swapped Items compared: [4, 6] => not swapped Items compared: [6, 0] => swapped [0, 6] Items compared: [6, 3] => swapped [3, 6] Items compared: [6, 5] => swapped [5, 6] Items compared: [6, 2] => swapped [2, 6] Items compared: [6, 7] => not swapped Items compared: [7, 8] => not swapped Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ] Items compared: [1, 4] => not swapped Items compared: [4, 0] => swapped [0, 4] Items compared: [4, 3] => swapped [3, 4] Items compared: [4, 5] => not swapped Items compared: [5, 2] => swapped [2, 5] Items compared: [5, 6] => not swapped Items compared: [6, 7] => not swapped Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ] Items compared: [1, 0] => swapped [0, 1] Items compared: [1, 3] => not swapped Items compared: [3, 4] => not swapped Items compared: [4, 2] => swapped [2, 4] Items compared: [4, 5] => not swapped Items compared: [5, 6] => not swapped Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ] Items compared: [0, 1] => not swapped Items compared: [1, 3] => not swapped Items compared: [3, 2] => swapped [2, 3] Items compared: [3, 4] => not swapped Items compared: [4, 5] => not swapped Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ] Items compared: [0, 1] => not swapped Items compared: [1, 2] => not swapped Items compared: [2, 3] => not swapped Items compared: [3, 4] => not swapped Output Array: [0 1 2 3 4 5 6 7 8 9 ]
//Java Code for Tower of Hanoi
import java.util.Arrays;
public class BubbleSort {
public static final int MAX = 10;
public static int[] list = {1, 8, 4, 6, 0, 3, 5, 2, 7, 9};
public static void display() {
System.out.print("[");
// navigate through all items
for (int i = 0; i < MAX; i++) {
System.out.print(list[i] + " ");
}
System.out.println("]");
}
public static void bubbleSort() {
boolean swapped;
// loop through all numbers
for (int i = 0; i < MAX - 1; i++) {
swapped = false;
// loop through numbers falling ahead
for (int j = 0; j < MAX - 1 - i; j++) {
System.out.print("Items compared: [" + list[j] + ", " + list[j + 1] + "] ");
// check if next number is lesser than current no
// swap the numbers.
// (Bubble up the highest number)
if (list[j] > list[j + 1]) {
int temp = list[j];
list[j] = list[j + 1];
list[j + 1] = temp;
swapped = true;
System.out.println("=> swapped [" + list[j] + ", " + list[j + 1] + "]");
} else {
System.out.println("=> not swapped");
}
}
// if no number was swapped that means
// array is sorted now, break the loop.
if (!swapped) {
break;
}
System.out.print("Iteration " + (i + 1) + "#: ");
display();
}
}
public static void main(String[] args) {
System.out.print("Input Array: ");
display();
System.out.println();
bubbleSort();
System.out.print("\nOutput Array: ");
display();
}
}
Output
Input Array: [1 8 4 6 0 3 5 2 7 9 ] Items compared: [1, 8] => not swapped Items compared: [8, 4] => swapped [4, 8] Items compared: [8, 6] => swapped [6, 8] Items compared: [8, 0] => swapped [0, 8] Items compared: [8, 3] => swapped [3, 8] Items compared: [8, 5] => swapped [5, 8] Items compared: [8, 2] => swapped [2, 8] Items compared: [8, 7] => swapped [7, 8] Items compared: [8, 9] => not swapped Iteration 1#: [1 4 6 0 3 5 2 7 8 9 ] Items compared: [1, 4] => not swapped Items compared: [4, 6] => not swapped Items compared: [6, 0] => swapped [0, 6] Items compared: [6, 3] => swapped [3, 6] Items compared: [6, 5] => swapped [5, 6] Items compared: [6, 2] => swapped [2, 6] Items compared: [6, 7] => not swapped Items compared: [7, 8] => not swapped Iteration 2#: [1 4 0 3 5 2 6 7 8 9 ] Items compared: [1, 4] => not swapped Items compared: [4, 0] => swapped [0, 4] Items compared: [4, 3] => swapped [3, 4] Items compared: [4, 5] => not swapped Items compared: [5, 2] => swapped [2, 5] Items compared: [5, 6] => not swapped Items compared: [6, 7] => not swapped Iteration 3#: [1 0 3 4 2 5 6 7 8 9 ] Items compared: [1, 0] => swapped [0, 1] Items compared: [1, 3] => not swapped Items compared: [3, 4] => not swapped Items compared: [4, 2] => swapped [2, 4] Items compared: [4, 5] => not swapped Items compared: [5, 6] => not swapped Iteration 4#: [0 1 3 2 4 5 6 7 8 9 ] Items compared: [0, 1] => not swapped Items compared: [1, 3] => not swapped Items compared: [3, 2] => swapped [2, 3] Items compared: [3, 4] => not swapped Items compared: [4, 5] => not swapped Iteration 5#: [0 1 2 3 4 5 6 7 8 9 ] Items compared: [0, 1] => not swapped Items compared: [1, 2] => not swapped Items compared: [2, 3] => not swapped Items compared: [3, 4] => not swapped Output Array: [0 1 2 3 4 5 6 7 8 9 ]
#Python Code for Tower of Hanoi
MAX = 10
list = [1, 8, 4, 6, 0, 3, 5, 2, 7, 9]
def display():
print("[", end="")
# navigate through all items
for i in range(MAX):
print(list[i], end=" ")
print("]")
def bubbleSort():
swapped = False
# loop through all numbers
for i in range(MAX - 1):
swapped = False
# loop through numbers falling ahead
for j in range(MAX - 1 - i):
print("Items compared: [",
list[j],
", ",
list[j + 1],
"] ",
end="")
# check if next number is lesser than the current number
# swap the numbers.
# (Bubble up the highest number)
if list[j] > list[j + 1]:
temp = list[j]
list[j] = list[j + 1]
list[j + 1] = temp
swapped = True
print("=> swapped [", list[j], ", ", list[j + 1], "]")
else:
print("=> not swapped")
# if no number was swapped, the array is sorted now, break the loop
if not swapped:
break
print("Iteration", (i + 1), "#: ", end="")
display()
print("Input Array: ", end="")
display()
print()
bubbleSort()
print("\nOutput Array: ", end="")
display()
Output
Input Array: [1 8 4 6 0 3 5 2 7 9 ] Items compared: [ 1 , 8 ] => not swapped Items compared: [ 8 , 4 ] => swapped [ 4 , 8 ] Items compared: [ 8 , 6 ] => swapped [ 6 , 8 ] Items compared: [ 8 , 0 ] => swapped [ 0 , 8 ] Items compared: [ 8 , 3 ] => swapped [ 3 , 8 ] Items compared: [ 8 , 5 ] => swapped [ 5 , 8 ] Items compared: [ 8 , 2 ] => swapped [ 2 , 8 ] Items compared: [ 8 , 7 ] => swapped [ 7 , 8 ] Items compared: [ 8 , 9 ] => not swapped Iteration 1 #: [1 4 6 0 3 5 2 7 8 9 ] Items compared: [ 1 , 4 ] => not swapped Items compared: [ 4 , 6 ] => not swapped Items compared: [ 6 , 0 ] => swapped [ 0 , 6 ] Items compared: [ 6 , 3 ] => swapped [ 3 , 6 ] Items compared: [ 6 , 5 ] => swapped [ 5 , 6 ] Items compared: [ 6 , 2 ] => swapped [ 2 , 6 ] Items compared: [ 6 , 7 ] => not swapped Items compared: [ 7 , 8 ] => not swapped Iteration 2 #: [1 4 0 3 5 2 6 7 8 9 ] Items compared: [ 1 , 4 ] => not swapped Items compared: [ 4 , 0 ] => swapped [ 0 , 4 ] Items compared: [ 4 , 3 ] => swapped [ 3 , 4 ] Items compared: [ 4 , 5 ] => not swapped Items compared: [ 5 , 2 ] => swapped [ 2 , 5 ] Items compared: [ 5 , 6 ] => not swapped Items compared: [ 6 , 7 ] => not swapped Iteration 3 #: [1 0 3 4 2 5 6 7 8 9 ] Items compared: [ 1 , 0 ] => swapped [ 0 , 1 ] Items compared: [ 1 , 3 ] => not swapped Items compared: [ 3 , 4 ] => not swapped Items compared: [ 4 , 2 ] => swapped [ 2 , 4 ] Items compared: [ 4 , 5 ] => not swapped Items compared: [ 5 , 6 ] => not swapped Iteration 4 #: [0 1 3 2 4 5 6 7 8 9 ] Items compared: [ 0 , 1 ] => not swapped Items compared: [ 1 , 3 ] => not swapped Items compared: [ 3 , 2 ] => swapped [ 2 , 3 ] Items compared: [ 3 , 4 ] => not swapped Items compared: [ 4 , 5 ] => not swapped Iteration 5 #: [0 1 2 3 4 5 6 7 8 9 ] Items compared: [ 0 , 1 ] => not swapped Items compared: [ 1 , 2 ] => not swapped Items compared: [ 2 , 3 ] => not swapped Items compared: [ 3 , 4 ] => not swapped Output Array: [0 1 2 3 4 5 6 7 8 9 ]
Fibonacci Series Using Recursion
Fibonacci series generates the subsequent number by adding two previous numbers. Fibonacci series starts from two numbers F0 & F1. The initial values of F0 & F1 can be taken 0, 1 or 1, 1 respectively.
Fibonacci series satisfies the following conditions −
Fn = Fn-1 + Fn-2
Hence, a Fibonacci series can look like this −
F8 = 0 1 1 2 3 5 8 13
or, this −
F8 = 1 1 2 3 5 8 13 21
For illustration purpose, Fibonacci of F8 is displayed as −

Fibonacci Iterative Algorithm
First we try to draft the iterative algorithm for Fibonacci series.
Procedure Fibonacci(n)
declare f0, f1, fib, loop
set f0 to 0
set f1 to 1
<b>display f0, f1</b>
for loop ← 1 to n
fib ← f0 + f1
f0 ← f1
f1 ← fib
<b>display fib</b>
end for
end procedure
Fibonacci Recursive Algorithm
Let us learn how to create a recursive algorithm Fibonacci series. The base criteria of recursion.
START
Procedure Fibonacci(n)
declare f0, f1, fib, loop
set f0 to 0
set f1 to 1
display f0, f1
for loop ← 1 to n
fib ← f0 + f1
f0 ← f1
f1 ← fib
display fib
end for
END
Example
#include <stdio.h>
int factorial(int n) {
//base case
if(n == 0) {
return 1;
} else {
return n * factorial(n-1);
}
}
int fibbonacci(int n) {
if(n == 0){
return 0;
} else if(n == 1) {
return 1;
} else {
return (fibbonacci(n-1) + fibbonacci(n-2));
}
}
int main() {
int n = 5;
int i;
printf("Factorial of %d: %d\n" , n , factorial(n));
printf("Fibbonacci of %d: " , n);
for(i = 0;i<n;i++) {
printf("%d ",fibbonacci(i));
}
}
Output
Factorial of 5: 120 Fibbonacci of 5: 0 1 1 2 3
// C++ Code for Fibonacci series
#include <iostream>
int factorial(int n) {
//base case
if(n == 0) {
return 1;
} else {
return n * factorial(n-1);
}
}
int fibbonacci(int n) {
if(n == 0){
return 0;
} else if(n == 1) {
return 1;
} else {
return (fibbonacci(n-1) + fibbonacci(n-2));
}
}
int main() {
int n = 5;
int i;
std::cout << "Factorial of " << n << ": " << factorial(n) << std::endl;
std::cout << "Fibbonacci of " << n << ": ";
for(i = 0;i<n;i++) {
std::cout << fibbonacci(i) << " ";
}
}
Output
Factorial of 5: 120 Fibbonacci of 5: 0 1 1 2 3
// Java Code for Fibonacci series
public class Fibonacci {
public static int factorial(int n) {
// base case
if (n == 0) {
return 1;
} else {
return n * factorial(n - 1);
}
}
public static int fibonacci(int n) {
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
} else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
public static void main(String[] args) {
int n = 5;
int i;
System.out.println("Factorial of " + n + ": " + factorial(n));
System.out.print("Fibonacci of " + n + ": ");
for (i = 0; i < n; i++) {
System.out.print(fibonacci(i) + " ");
}
}
Output
Factorial of 5: 120 Fibonacci of 5: 0 1 1 2 3
#Python code for fibonacci Series
def factorial(n):
# base case
if n == 0:
return 1
else:
return n * factorial(n-1)
def fibonacci(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
if __name__ == "__main__":
n = 5
print("Factorial of", n, ":", factorial(n))
print("Fibonacci of", n, ": ")
for i in range(n):
print(fibonacci(i))
Output
Factorial of 5 : 120 Fibonacci of 5 : 0 1 1 2 3